四象很直线逐点比较法插补计算 第二四象限内的由坐标原点出发的直线的插补运 算,可由第一象限插补公式得到。 +y E2(-xgyg) E(xE>YE) 图8.22 F<0 F≥0 F≥0 F<0 四象限直线插 一十x 补误差函数与 进给方向 R<0 F≥0 F0 F<0 E3(-XE:-yg) E4(xE:-Yg) F20 F<0 所在象限 进给方向 误差函数计算公式 进给方向 误差函数计算公式 第一象限 +x 第二象限 x 第三象限 x FFFrye y F-FAXE 第四象限 +x y
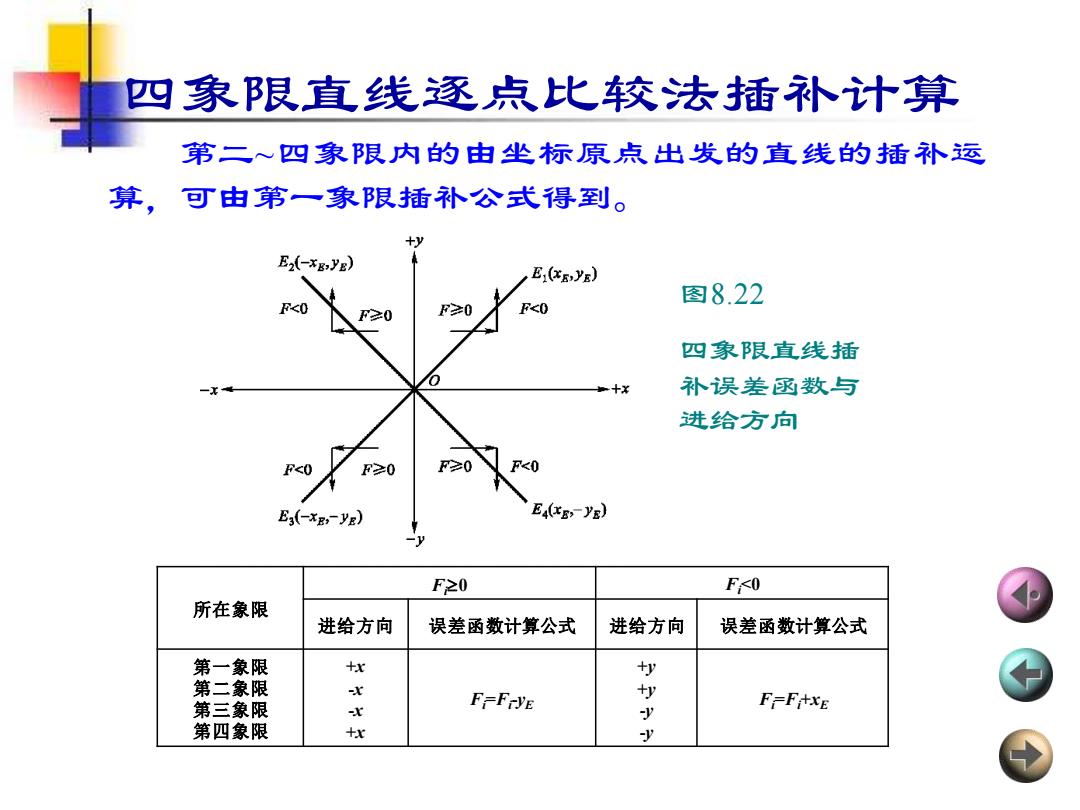
四象限直线逐点比较法插补计算 第二~四象限内的由坐标原点出发的直线的插补运 算,可由第一象限插补公式得到。 图8.22 四象限直线插 补误差函数与 进给方向 所在象限 Fi0 Fi<0 进给方向 误差函数计算公式 进给方向 误差函数计算公式 第一象限 第二象限 第三象限 第四象限 +x -x -x +x Fi=Fi -yE +y +y -y -y Fi=Fi+xE

圆孤逐点比较去插补 假定要加工第一象限内以坐标原点为圆心的圆弧AB,圆弧起 点坐标A(x和y人终点坐标为B(xB,yB),这是一个逆时针圆弧,简 称为逆圆。 由所给条件知,圆弧半径R满足 √误差判别 R2=x2+y2=x8+y2 √坐标进给 √误差计算 设当前加工点为(x,y),定义圆弧插补的误差函数为 √终点判断 F=x2+y2-R2 若规定F0时,向一x轴方向 B(xgYg) /I(x,:) 进给,为了逼近圆弧,则有: 向一x轴方向进给的条件为F≥0 F41=x+y2-R2=E-2x,+1 R A(xAYA) 向+y轴方向进给的条件为<0 F+1=x异1+y品1-R2=F+2y+1 图8.23第一象限逆圆插补原理
圆弧逐点比较法插补 假定要加工第一象限内以坐标原点为圆心的圆弧AB,圆弧起 点坐标A(xA,yA )、终点坐标为B(xB,yB ),这是一个逆时针圆弧,简 称为逆圆。 由所给条件知,圆弧半径R满足 设当前加工点为I(xi,yi ),定义圆弧插补的误差函数为 2 2 2 2 2 R x y x y = + = + A A B B 2 2 2 Fi = xi + yi − R 图8.23第一象限逆圆插补原理 若规定Fi=0时,向﹣x轴方向 进给,为了逼近圆弧,则有: 向﹣x轴方向进给的条件为Fi≥0 向 + y轴方向进给的条件为Fi<0 2 1 2 2 1 2 Fi+1 = xi+1 + yi+ − R = Fi − xi + 2 1 2 2 1 2 Fi+1 = xi+1 + yi+ − R = Fi + yi + ✓误差判别 ✓坐标进给 ✓误差计算 ✓终点判断
圆弧插补示例 第一象限的逆圆AB,起点 A的坐标为(4,0),终点B 的坐标为(0,4),圆心在 坐标原点 2 3 4 步数 误差判别 坐标进给 误差计算 动点坐标计算 终点判别 初始化 F-0 =4,J=0 ΣH4-01+H0-4=8 F-0 x F=F-2x+1=7 x-1=3,y不变 =Σ-1=7 2 F<0 y F=F+2y+1=-6 与+1=1,x不变 ∑-=X16 F<0 y F=F+2y+1=3 与y+1=2,x不变 =∑-1-5 4 F<0 y F=F42+1=2 +1=3,x不变 =Σ1=4 5 F>0 x F=F-2r+1=3 x-1=2,y不变 =2-1-3 6 F<0 y F=F+2y+1=4 J与y+1=4,x不变 =-1-2 7 F>0 x F=F-2x+1=1 x-1=l,y不变 =81=1 F>0 x F=F-2x+1-0 x式-1=0,y不变 ∑0,停止插补
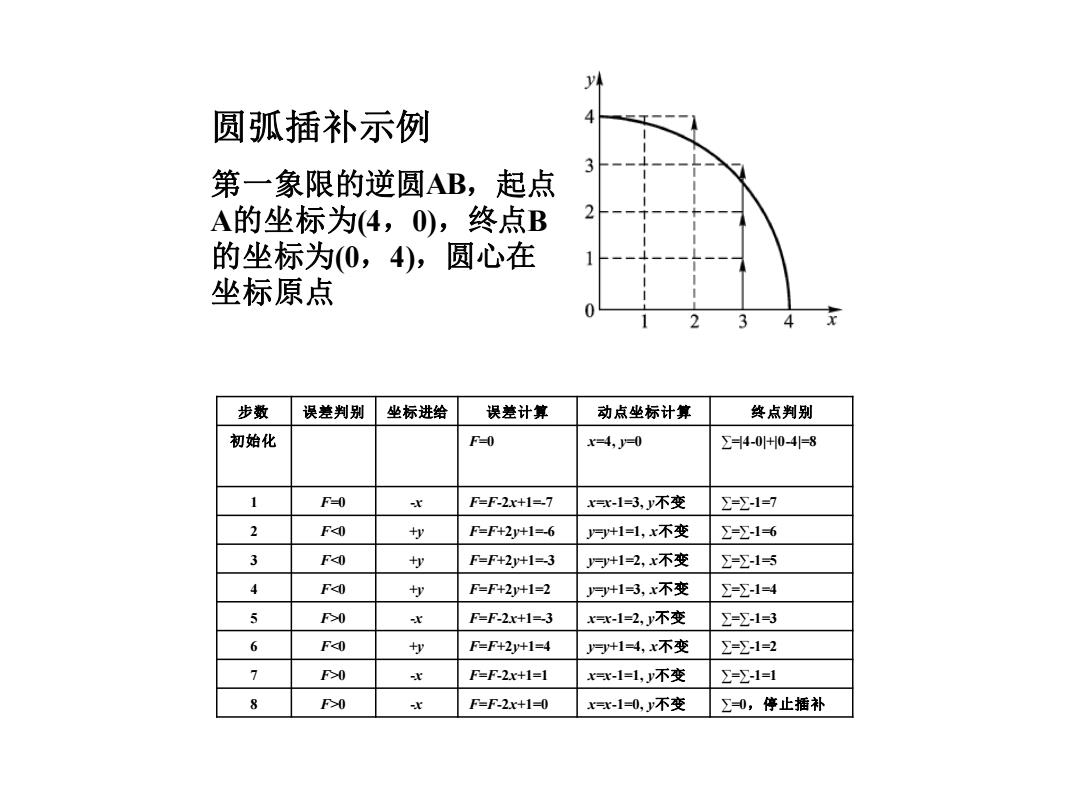
步数 误差判别 坐标进给 误差计算 动点坐标计算 终点判别 初始化 F=0 x=4, y=0 ∑=|4-0|+|0-4|=8 1 F=0 -x F=F-2x+1=-7 x=x-1=3, y不变 ∑=∑-1=7 2 F<0 +y F=F+2y+1=-6 y=y+1=1, x不变 ∑=∑-1=6 3 F<0 +y F=F+2y+1=-3 y=y+1=2, x不变 ∑=∑-1=5 4 F<0 +y F=F+2y+1=2 y=y+1=3, x不变 ∑=∑-1=4 5 F>0 -x F=F-2x+1=-3 x=x-1=2, y不变 ∑=∑-1=3 6 F<0 +y F=F+2y+1=4 y=y+1=4, x不变 ∑=∑-1=2 7 F>0 -x F=F-2x+1=1 x=x-1=1, y不变 ∑=∑-1=1 8 F>0 -x F=F-2x+1=0 x=x-1=0, y不变 ∑=0,停止插补 圆弧插补示例 第一象限的逆圆AB,起点 A的坐标为(4,0),终点B 的坐标为(0,4),圆心在 坐标原点
四象限圆弧逐点比较法插补计算公式 F20 F<0 进给方 误差计算 动点坐标 进给方 向 向 误差计算 动点坐标 第一象限顺圆 少 +x 第三象限顺圆 ty Xi+l-Xi -x 第二象限逆圆 F-F 2y1 i=1 F=F+2x+1 x+1x+1 沙 x Jy》+1y: 第四象限逆圆 ty +x 第一象限逆圆 -x y 第三象限逆圆 +x F=F-2x+1 七#1=x-1 y xi41式i 第二象限顺圆 +x F=F+2y+1 yiI i y#1y汁1 第四象限顺圆 -北 y
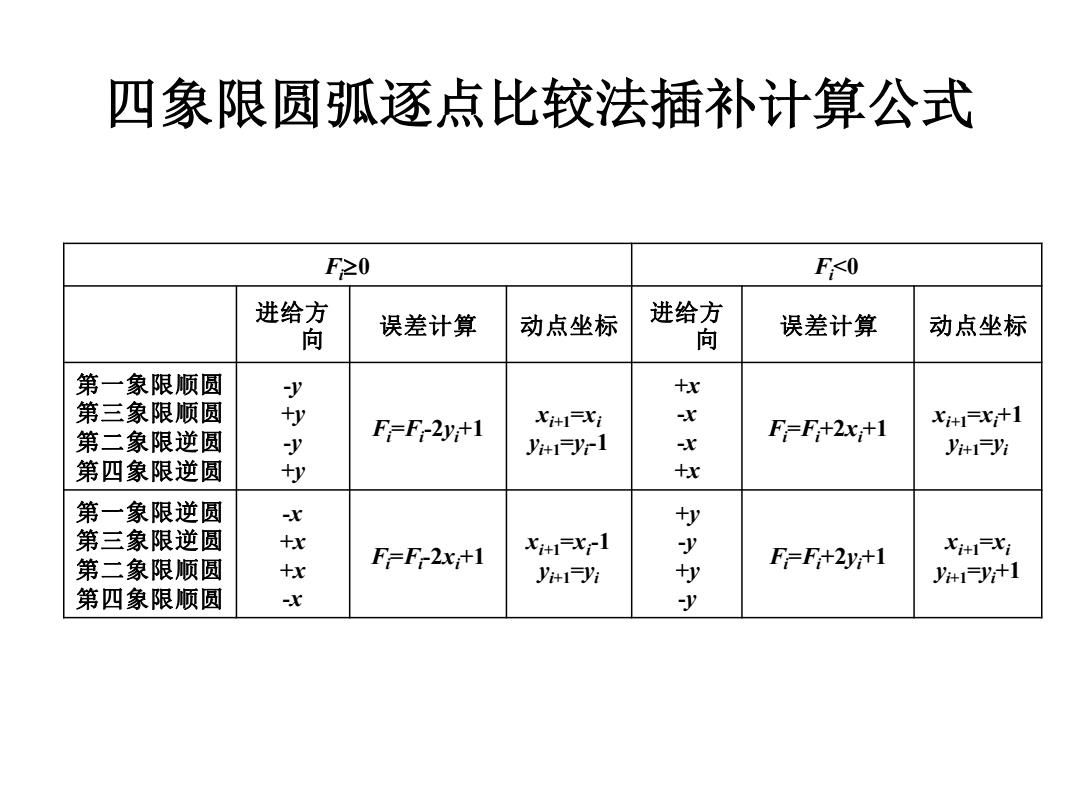
四象限圆弧逐点比较法插补计算公式 Fi0 Fi<0 进给方 向 误差计算 动点坐标 进给方 向 误差计算 动点坐标 第一象限顺圆 第三象限顺圆 第二象限逆圆 第四象限逆圆 -y +y -y +y Fi=Fi -2yi+1 xi+1=xi yi+1=yi -1 +x -x -x +x Fi=Fi+2xi+1 xi+1=xi+1 yi+1=yi 第一象限逆圆 第三象限逆圆 第二象限顺圆 第四象限顺圆 -x +x +x -x Fi=Fi -2xi+1 xi+1=xi -1 yi+1=yi +y -y +y -y Fi=Fi+2yi+1 xi+1=xi yi+1=yi+1

2,步进电机控制 步进电机是计算机控制系统常用的执行元 件,具有快速起停、精确步进的特点,并可直 接采用数字脉冲信号控制,而不需要进行AD 转换,因而为控制系统的设计带来极大的方便。 0 步进电机的工作原理 口步进电机的计算机控制
2. 步进电机控制 步进电机是计算机控制系统常用的执行元 件,具有快速起停、精确步进的特点,并可直 接采用数字脉冲信号控制,而不需要进行A/D 转换,因而为控制系统的设计带来极大的方便。 ❑ 步进电机的工作原理 ❑ 步进电机的计算机控制