
0
o x y o x y
0
o x y o x y

>增量 △u=u2-4 f(x) ●注(1)△可正可负 f(xO+△x) △u>0→u2>u1 f(xo △u=0→2=41 △u<0→u2<4 0 (2) △u是一个整体记号 (△u2≠△2 △y=f(x+△x)-f(xo) >定义1设函数f(x)在点xo的某一邻域内有定义,如果 Iim△y=lim[f(x+△x)-f(xo)]=0 Ar- 那么就称函数f(x)在点x。连续 ●注 在定义式中,Ax为变量xo要视为常量. ◆例1证明y=sinx在x,(x,∈R)处连续
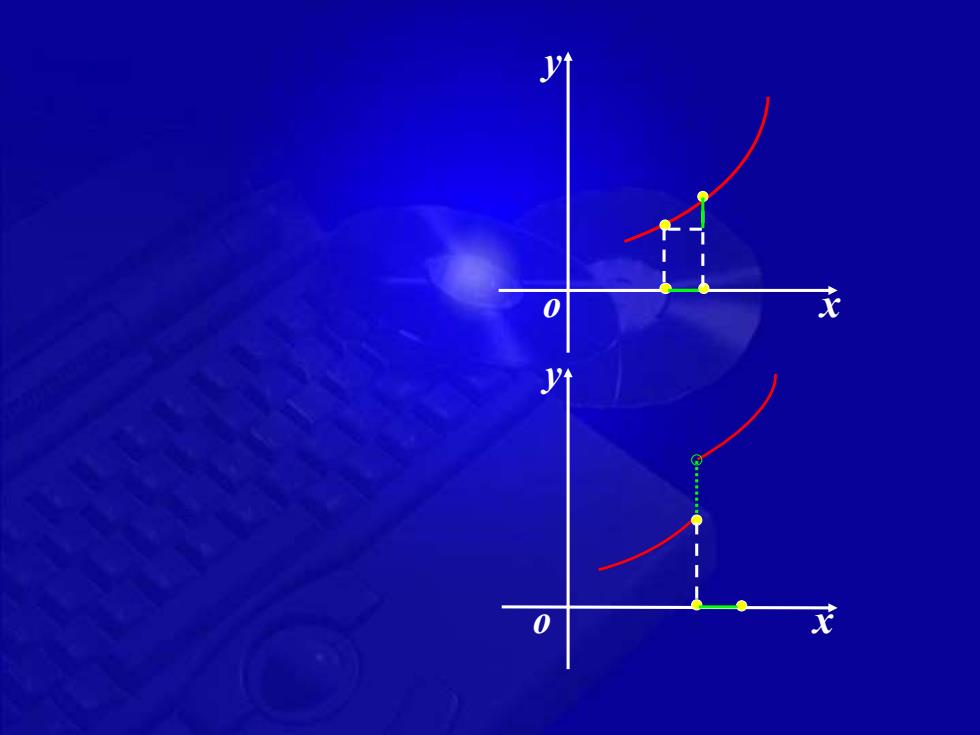
x y o u = u2 − u1 ➢增量 u 0 u2 u1 u = 0 u2 = u1 u 0 u2 u1 ⚫注 (1) u 可正可负 (2) u 是一个整体记号 ( ) 2 2 u u x0 x + x 0 f (x + x) 0 ( ) 0 f x f (x) ( ) ( ) 0 0 y = f x + x − f x ➢定义1 设函数f (x)在点x0的某一邻域内有定义,如果 0 0 0 0 lim lim ( ) ( ) 0 x x y f x x f x → → = + − = 那么就称函数f (x)在点x0连续. ⚫注 在定义式中,Δx为变量,x0要视为常量. ◆例1 证明y = sin x在 ( R) x0 x0 处连续

(一)函数在一点处连续的概念 1.定义1 2. 定义2 3.定义3 4.左连续与右连续 5.1 性质
(一)函数在一点处连续的概念 1.定义1 2.定义2 3.定义3 4.左连续与右连续 5.性质

(一)函数在一点处连续的概念 1,定义1 2.定义2 3.定义3 4.左连续与右连续 5.性质
(一)函数在一点处连续的概念 1.定义1 2.定义2 3.定义3 4.左连续与右连续 5.性质