
料力学教案第36讲教学方案静不定系统(II)基本1.对称条件的利用。内容2.连续梁与三弯矩方程(简介)教1.了解对称结构的对称变形与反对称变形基本概念学目掌握对称结构的对称变形与反对称变形性质的利用。2.的3.掌握对于某些载荷既非对称,也非反对称,但可将它们化成对称和反对称两种情况的叠加,以使问题简化。4.初步掌握连续梁静不定次数的判定、三弯矩方程组的建立及其解法。重点掌握对称结构的对称变形与反对称变形性质的利用重2.重点掌握如何将非对称载荷作用下的静不定问题化简计点、难算。难点是建立正确的简化方案。点3.解连续梁问题的难点是正确建立三弯矩方程组、及方程中各3.个系数的计算。本次教学计划学时:2学时。教学课堂讨论:安
材 料 力 学 教 案 第 36 讲 教学方案 —— 静不定系统(Ⅱ) 基 本 内 容 1. 对称条件的利用。 2. 连续梁与三弯矩方程(简介)。 教 学 目 的 1. 了解对称结构的对称变形与反对称变形基本概念。 2. 掌握对称结构的对称变形与反对称变形性质的利用。 3. 掌握对于某些载荷既非对称,也非反对称,但可将它们化 成对称和反对称两种情况的叠加,以使问题简化 。 4. 初步掌握连续梁静不定次数的判定、三弯矩方程组的建立及 其解法 。 重 点 、 难 点 1. 重点掌握对称结构的对称变形与反对称变形性质的利用 。 2. 重点掌握如何将非对称载荷作用下的静不定问题化简计 算 。难点是建立正确的简化方案。 3. 解连续梁问题的难点是正确建立三弯矩方程组、及方程中各 个系数的计算。 教 学 安 本次教学计划学时:2 学时。 课堂讨论:

三十六讲排1.如何建立正确的简化方案,将某些载荷既非对称,也非反对称,但可将它们化成对称和反对称两种情况的叠加,以使问题简化2.在解连续梁问题中如何处理边界条件?3.在解连续梁问题中如何应用图乘法?
第 三 十 六 讲 排 1. 如何建立正确的简化方案,将某些载荷既非对称,也非反 对称,但可将它们化成对称和反对称两种情况的叠加,以使问题 简化 2.在解连续梁问题中如何处理边界条件? 3.在解连续梁问题中如何应用图乘法?

大迎为尚欢店s14-3对称及反对称性质的利用1.对称结构的对称变形与反对称变形结构几何尺寸、形状,构件材料及约束条件均对称于某一轴,则称此结构为对称结构(图12-8a)。当对称结构受力也对称于结构对称轴,则此结构将产生对称变形(图12-8b)。如外力反对称于结构对称轴,则结构将产生反对称变形(图12-8c)。正确利用对称、反对称性质,则可推知某些未知量,可大大简化计算过程:如对称变形对称截面上(图12-8b),反对称内力等于零或已知;反对称变形(图12-8c)反对称截面上,对称内力M为零或已知。TTFTT图 12-8对称结构的对称变形与反对称变形2.对称变形以图12-9(a)对称变形为例,切开结构对称截面,此为三次超静定,应有三个多余未知力,即轴力X,,弯矩X,与剪力X,。可证明其反对称内力X,应为零,正则方程为:(a)8,X +0X, +0,X +4p =0(b)821X, +822X, +02,X, +A2p = 0,X, +832X, +03,X, +A3p =0(c)用图乘法计算8,及A,p(i=1,2,3)时,所要用的载荷弯矩图M,以及X,=1,X,=1,X,=1时的弯矩图分别见图12-9、(c)、(d)、(e)、(f),其中Mp,M,,M,均对称于对称轴,而M,反对称于对称轴。由莫尔积分知对称函数与反对称函数相乘在区间积分应为零,即有:[M,Mdx=0, 1 =8,1 =[MMdx=0, 62=02=]M,Mdx=0A3p =[EIJIEIJIEI
材 料 力 学 教 案 §14-3 对称及反对称性质的利用 1.对称结构的对称变形与反对称变形 结构几何尺寸、形状,构件材料及约束条件均对称于某一轴,则称此结构为对称结构(图 12-8a)。 当对称结构受力也对称于结构对称轴,则此结构将产生对称变形(图 12-8b)。如外力反 对称于结构对称轴,则结构将产生反对称变形(图 12-8c)。 正确利用对称、反对称性质,则可推知某些未知量,可大大简化计算过程:如对称变形 对称截面上(图 12-8b),反对称内力 Q 等于零或已知;反对称变形(图 12-8c)反对称截 面上,对称内力 M 为零或已知。 2.对称变形 以图 12-9(a)对称变形为例,切开结构对称截面,此为三次超静定,应有三个多余未 知力,即轴力 X1 ,弯矩 X2 与剪力 X 3 。可证明其反对称内力 X 3 应为零,正则方程 为: 11X1 + 12X2 + 13X3 + 1P = 0 (a) 21X1 + 22X2 + 23X3 + 2P = 0 (b) 31X1 + 32X2 + 33X3 + 3P = 0 (c) 用图乘法计算 ij 及 (i = 1,2,3) iP 时,所要用的载荷弯矩图 MP 以及 X1 =1,X2 =1, X3 = 1 时的弯矩图分别见图 12-9、(c)、(d)、(e)、(f),其中 MP ,M1,M2 均对称于对 称轴,而 M3 反对称于对称轴。由莫尔积分知对称函数与反对称函数相乘在区间积分应为零, 即有: 0 3 3 = = l P P dx EI M M , 0 1 3 13 = 31 = = l dx EI M M , 0 2 3 23 = 32 = = l dx EI M M
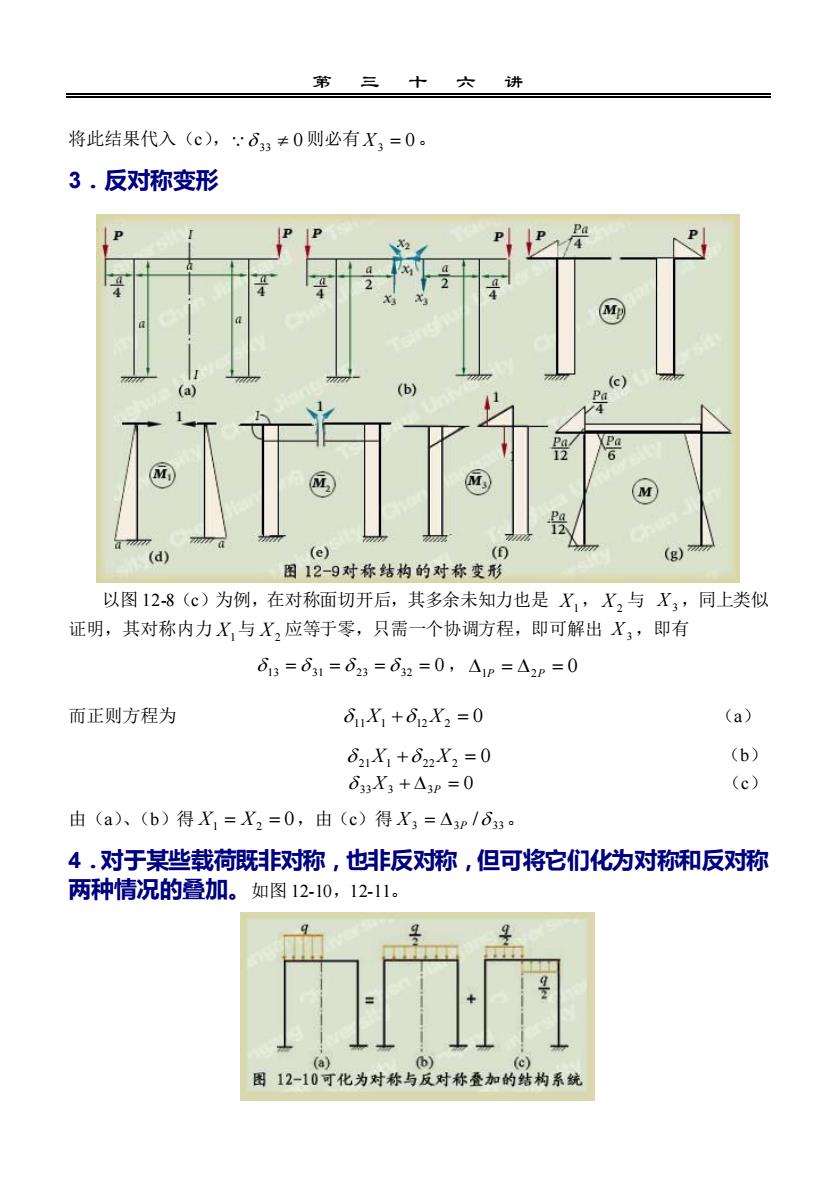
第川六将此结果代入(c),:833¥0则必有X,=0。3.反对称变形TA图12-9对称结构的对称变形以图12-8(c)为例,在对称面切开后,其多余未知力也是X,X,与X,,同上类似证明,其对称内力X,与X,应等于零,只需一个协调方程,即可解出X,,即有013=03=023=02=0, A1p=2p=0(a)而正则方程为8X, +812X,=0(b)82,X +822X, =0(c)X,+3p=0由(a)、(b)得X,=X,=0,由(c)得X,=A3p/83。4.对于某些载荷既非对称,也非反对称,但可将它们化为对称和反对称两种情况的叠加。如图 12-10,12-11。图 12-10可化为对称与反对称叠加的结构系统
第 三 十 六 讲 将此结果代入(c), 33 0 则必有 X3 = 0。 3.反对称变形 以图 12-8(c)为例,在对称面切开后,其多余未知力也是 X1,X2 与 X 3 ,同上类似 证明,其对称内力 X1 与 X2 应等于零,只需一个协调方程,即可解出 X 3 ,即有 13 = 31 = 23 = 32 = 0 ,1P = 2P = 0 而正则方程为 11X1 + 12X2 = 0 (a) 21X1 + 22X2 = 0 (b) 33X3 + 3P = 0 (c) 由(a)、(b)得 X1 = X2 = 0 ,由(c)得 3 3 33 X = P / 。 4.对于某些载荷既非对称,也非反对称,但可将它们化为对称和反对称 两种情况的叠加。如图 12-10,12-11

留12-11可化为对称与反对称的情形(b()(d)e图12-12圆环受一对力P例14-3半径为R的圆环,直径CD方向受一对力P(图12-12a),求圆环内弯矩M。解:(1)超静定次数:封闭圆环为三次超静定。在A处截开,则有三个多余未知力,弯矩X,轴力X,,剪力X,(图12-12b)。(2)对称性:直径AB为一对称轴,对称截面A上剪力X,应为零,对称截面B上弯矩和轴力与截面A上相等。由竖直方向力的平衡可得X,=P/2。故只有弯矩X未知(图c).(3)选半圆环为静定基,作用于半圆环的力如图(c),则协调条件应是A或B截面在P及弯矩X,作用下转角θ应为零(由对称性可知),所以有(a),X +4p=0(4)84p计算静定基上施加外力P如图(d)及单位力偶如图(e),用莫尔法求S与4p。单位力偶引起弯矩:=1,(0)PR(1-cosa), (o≤)外力引起弯矩:Mp=根据对称性,可只取1/4圆环进行计算,故有
材 料 力 学 教 案 例 14-3 半径为 R 的圆环,直径 CD 方向受一对力 P (图 12-12a),求圆环内弯矩 M 。 解:(1)超静定次数:封闭圆环为三次超静定。在 A 处截开,则有三个多余未知力,弯 矩 X1 ,轴力 X2 ,剪力 X3 (图 12-12b)。 (2)对称性:直径 AB 为一对称轴,对称截面 A 上剪力 X 3 应为零,对称截面 B 上弯 矩和轴力与截面 A 上相等。由竖直方向力的平衡可得 X2 = P/ 2 。故只有弯矩 X1 未知(图 c)。 (3)选半圆环为静定基,作用于半圆环的力如图(c),则协调条件应是 A 或 B 截面在 P 及弯矩 X1 作用下转角 应为零(由对称性可知),所以有 11X1 + 1P = 0 (a) (4) 11 , 1P 计算 静定基上施加外力 P 如图(d)及单位力偶如图(e),用莫尔法求 11 与 1P 。 单位力偶引起弯矩: M =1,(0 ) 外力引起弯矩: (1 cos) 2 = − PR M P , 2 0 根据对称性,可只取 1/4 圆环进行计算,故有