
材料力学教案第32讲 教学方案能量法(I)基本内1.变形能的普遍表达式。容2.莫尔积分。教1.掌握外力功、变形能的计算方法。学目2了解应变余功,应变余能的基本概念,的掌握由能量原理导出的能量法、莫尔积分公式的导出。3.4.4.会计算五种基本变形状态下的变形能的计算5.了解非线性弹性材料构件的变形功、变形能的计算,广义力、广义位移、克拉贝依隆原理的概念。1.重点掌握外力功、变形能的计算方法。重点、难上2.重点掌握能量法的基本原理。3.要求熟练掌握五种基本变形状态下的变形能的计算。点难点之一是莫尔积分公式的正确应用。4.5.难点之二是莫尔积分公式应用的推广本次教学计划学时:2学时。教学课堂讨论:安排1.外力功与变形能之间的关系。2.小变形条件制约了什么?
材 料 力 学 教 案 第 32 讲 教学方案 —— 能量法(Ⅰ) 基 本 内 容 1. 变形能的普遍表达式。 2. 莫尔积分。 教 学 目 的 1. 掌握外力功、变形能的计算方法。 2. 了解应变余功,应变余能的基本概念。 3. 掌握由能量原理导出的能量法、莫尔积分公式的导出。 4. 会计算五种基本变形状态下的变形能的计算。 5. 了解非线性弹性材料构件的变形功、变形能的计算,广义 力、广义位移、克拉贝依隆原理的概念。 重 点 、 难 点 1. 重点掌握外力功、变形能的计算方法。 2. 重点掌握能量法的基本原理。 3. 要求熟练掌握五种基本变形状态下的变形能的计算。 4. 难点之一是莫尔积分公式的正确应用。 5. 难点之二是莫尔积分公式应用的推广。 教 学 安 排 本次教学计划学时:2 学时。 课堂讨论: 1. 外力功与变形能之间的关系。 2. 小变形条件制约了什么?

常3.引出单位载荷法与莫尔积分的关系
第 三 十 二 讲 3. 引出单位载荷法与莫尔积分的关系
索材料力学教第十三章能量原理及其应用s13-1外力功变形能1.变形功与变形能弹性杆受拉力P作用(图11-1),当P从零开始到终值P缓慢加载时,力P在其作用方向上的相应位移也由零增至A,而做功,称为变形功。W=I"Pds(13-1)与此同时弹性杆被拉长△I,而具有做功的能力,表明杆件内储存了变形能。单位体积储存的应变能称为应变比O熊u=f'adse(13-2)整个杆件的变形能为图11-1非线性材料拉杆的P-AU-[udy(13-3)曲线、a-e关系与变形能如果略去拉伸过程中的动能及其它能量的变化与损失由能量守恒原理,杆件的变形能U在数值上应等于外力做的功W,即有U-W(13-4)这是一个对变形体都适用的普遍原理称为功能原理,弹性固体变形是可逆的,即当外力解除后,弹性体将恢复其原来形状,释放出变形能而做功。但当超出了弹性范围,具有塑性变形的固体,变形能不能全部转变为功,因为变形体产生塑性变形时要消耗一部分能量,留下残余变形。2.应变余功与余能P.6APT图11-2非线性材料拉杆的P-△、G-e曲线与余能
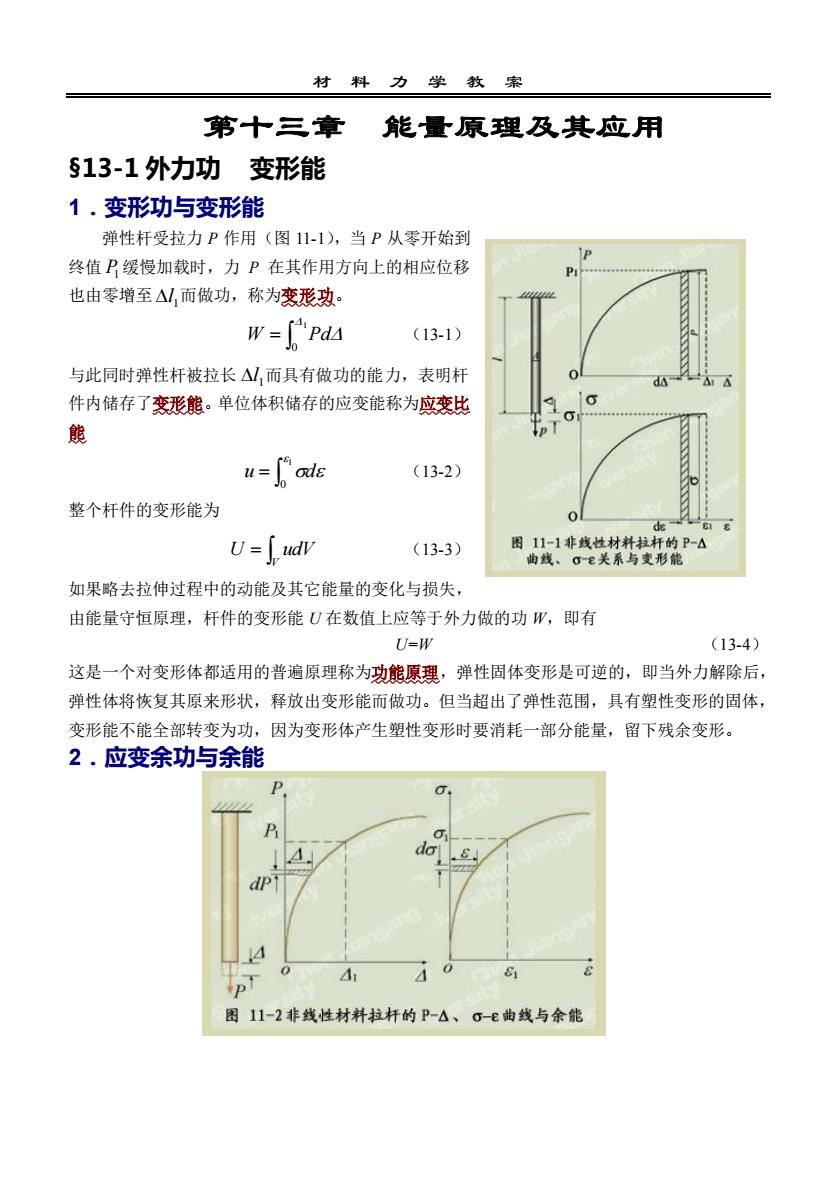
材 料 力 学 教 案 第十三章 能量原理及其应用 §13-1 外力功 变形能 1.变形功与变形能 弹性杆受拉力 P 作用(图 11-1),当 P 从零开始到 终值 P1 缓慢加载时,力 P 在其作用方向上的相应位移 也由零增至 1 l 而做功,称为变形功。 = 1 0 W Pd (13-1) 与此同时弹性杆被拉长 1 l 而具有做功的能力,表明杆 件内储存了变形能。单位体积储存的应变能称为应变比 能 = 1 0 u d (13-2) 整个杆件的变形能为 = V U udV (13-3) 如果略去拉伸过程中的动能及其它能量的变化与损失, 由能量守恒原理,杆件的变形能 U 在数值上应等于外力做的功 W,即有 U=W (13-4) 这是一个对变形体都适用的普遍原理称为功能原理,弹性固体变形是可逆的,即当外力解除后, 弹性体将恢复其原来形状,释放出变形能而做功。但当超出了弹性范围,具有塑性变形的固体, 变形能不能全部转变为功,因为变形体产生塑性变形时要消耗一部分能量,留下残余变形。 2.应变余功与余能

变形体受外力作用时的余劲定义为W.=I" sdpP其中Pi是外力从零增加到的终值,仿照功与变形能相等的关系,将余功相应的能称为余能,用U.表示。余功与余能相等,即U,=W,- I"dp可仿照前面,定义单位体积余应变能(或应变余能),称为余应变比熊u. = [" do由此整个结构余应变熊可写成U,=[ u.dv应指出:余功、余应变能、余应变比能具有功的量纲,是变形体的另一能量参数,但都没有具体的物理概念,只是常力所做的功减去变力所做功余下的那部分功。3.能量原理固体力学中运用功与能有关的基本原理统称为熊量原理,由此发展出来的方法称为熊量法能量原理是在总体上从功与能的角度考察变形体系统的受力、应力与变形的原理与方法,是进一步学习固体力学的基础,也是当今应用甚广的有限元法求解力学问题的重要基础。4。本章内容本章只涉及能量原理在材料力学中常用的部分内容,如:变形熊、再等定理、卡氏定理、惠功原理、单位载荷法及图乘法,更为深入的,如最小势能原理,最小余能原理等变分原理,可参考其它专著。s13-2外力功和变形能计算to杆件不同受力情况下的变形能1.轴向拉伸或压缩线弹性杆件(图11-3)拉、压杆应变比熊lg2或=E82=0s=(13-5)2E5图11-3拉压杆的o-e关系曲线
第 三 十 二 讲 变形体受外力作用时的余功定义为 = 1 0 P Wc dP 其中 P1 是外力从零增加到的终值,仿照功与变形能相等的关系,将余功相应的能称为余能,用 Uc表示。余功与余能相等,即 = = 1 0 P Uc Wc dP 可仿照前面,定义单位体积余应变能(或应变余能),称为余应变比能 = 1 0 uc d 由此整个结构余应变能可写成 U u dV V c = c 应指出:余功、余应变能、余应变比能具有功的量纲,是变形体的另一能量参数,但都没 有具体的物理概念,只是常力所做的功减去变力所做功余下的那部分功。 3.能量原理 固体力学中运用功与能有关的基本原理统称为能量原理,由此发展出来的方法称为能量法。 能量原理是在总体上从功与能的角度考察变形体系统的受力、应力与变形的原理与方法,是进一 步学习固体力学的基础,也是当今应用甚广的有限元法求解力学问题的重要基础。 4.本章内容 本章只涉及能量原理在材料力学中常用的部分内容,如:变形能、互等定理、卡氏定理、虚 功原理、单位载荷法及图乘法,更为深入的,如最小势能原理,最小余能原理等变分原理,可参 考其它专著。 §13-2 外力功和变形能计算 杆件不同受力情况下的变形能。 1.轴向拉伸或压缩线弹性杆件(图 11-3) 拉、压杆应变比能 E u 2 2 1 2 1 = = 或 2 2 1 E (13-5)

材料力学教案则整个杆的变形能rN"(x)dU= [, udV =f'(13-6)dAdx=J.JA2E2EA其中α,N是内力(轴力),A是截面面积,1是杆长。对于等截面杆,内力N=P=常数,用(13-1),线弹性范围内拉压杆的变形能U=W-,PN而杆的伸长(或缩短)A=上式可改写成EAU=W-!p}(13-7)2 EA2.纯剪,扭转线弹性杆件(图11-4)OB图11-4扭转杆的扭矩m与扭转角中的关系面线线弹性材料纯剪应力状态杆件的应变比能为或=Ey(13-8)U=TO扭转杆的变形能TprT?(x)dU- JrdV=IL2GdAdx = I"JL2Gr,_dAdx =(13-9)Jo2GI,其中I。=,p’dA,(x)是截面上的扭矩(内力)。对于受扭转力偶矩m作用的等截面圆杆,如果杆件材料是线弹性的,则其扭转角为
材 料 力 学 教 案 则整个杆的变形能 dx EA N x dAdx E U udV l V l A = = = 0 2 0 2 2 ( ) 2 (13-6) 其中 A N = ,N 是内力(轴力),A 是截面面积,l 是杆长。 对于等截面杆,内力 N=P=常数,用(13-1),线弹性范围内拉压杆的变形能 U = W = Pl 2 1 而杆的伸长(或缩短) EA Pl l = ,上式可改写成 EA P l U W 2 2 1 = = (13-7) 2.纯剪,扭转线弹性杆件(图 11-4) 线弹性材料纯剪应力状态杆件的应变比能为 G u 2 2 1 2 = = 或 2 2 1 E (13-8) 扭转杆的变形能 dAdx G U udV l V A = = 0 2 2 dAdx GI l T A = 0 2 2 2 2 dx GI l T x = 0 2 2 ( ) (13-9) 其中 I dA A = 2 ,T(x)是截面上的扭矩(内力)。 对于受扭转力偶矩 m 作用的等截面圆杆,如果杆件材料是线弹性的,则其扭转角为