
材料力学教案第27讲教学方案压杆稳定(II)/基本内容1.非细长杆的经验公式;2.临界应力总图3.压杆的稳定校核;4.安全系数法与稳定系数法;5.提高压杆稳定性的措施
材 料 力 学 教 案 第 27 讲 教学方案 —— 压杆稳定(Ⅱ) 基 本 内 容 1.非细长杆的经验公式;2.临界应力总图; 3.压杆的稳定校核; 4. 安全系数法与稳定系数法; 5. 提高压杆稳定性的措施

A+七茶教学1.明确欧拉公式只有在弹性范围内才是适用的;目的2.了解非细长杆的经验公式的导出方法;3.掌握临界应力总图的概念及其应用;4.说明提高压杆稳定性的每一项措施都是结合欧拉公式给出的。对每一措施给出具体的示例。1.重点掌握欧拉公式只有在弹性范围。重点2.掌握提高压杆稳定性的每一项措施的理论根据。难3.掌握细长杆、中长杆、短粗杆的划分界限。点4。难点是安全系数法与稳定系数法的应用。本次教学计划学时:2学时。课堂讨论:教学1.将细长压杆由低碳钢材料改变为中碳钢、高碳钢或合金钢安会提高临界载荷吗?为什么?简单复习钢材的力学性能。排2.截面的合理设计在梁的问题中已经讲过,主要是增加惯性矩这里要考虑对不同坐标轴的惯性矩,给出思考题,复习一遍3.加强约束,即减小长度系数μ;减小长度,可加中间支撑分别给出实例
第 二 十 七 讲 教 学 目 的 1. 明确欧拉公式只有在弹性范围内才是适用的; 2. 了解非细长杆的经验公式的导出方法; 3. 掌握临界应力总图的概念及其应用; 4. 说明提高压杆稳定性的每一项措施都是结合欧拉公式给出 的。对每一措施给出具体的示例。 重 点 、 难 点 1. 重点掌握欧拉公式只有在弹性范围。 2. 掌握提高压杆稳定性的每一项措施的理论根据。 3. 掌握细长杆、中长杆、短粗杆的划分界限。 4. 难点是安全系数法与稳定系数法的应用。 教 学 安 排 本次教学计划学时:2 学时。 课堂讨论: 1.将细长压杆由低碳钢材料改变为中碳钢、高碳钢或合金钢, 会提高临界载荷吗?为什么? 简单复习钢材的力学性能。 2.截面的合理设计在梁的问题中已经讲过,主要是增加惯性 矩,这里要考虑对不同坐标轴的惯性矩,给出思考题,复习一遍。 3.加强约束,即减小长度系数 ;减小长度,可加中间支撑; 分别给出实例

材料力学教案$9-4欧拉公式的适用范围如上节所述,欧拉公式只有在弹性范围内才是适用的。为了判断压杆失稳时是否处于弹性范围,以及超出弹性范围后临界力的计算问题,必须引入临界应力及柔度的概念。压杆在临界力作用下,其在直线平衡位置时横截面上的应力称为临界应力,用。表示。压杆在弹性范围内失稳时,则临界应力为:Pa元EI元EP_元E(15-3)dr2-2A(ul)"A(μl)?式中允称为柔度,i为截面的惯性半径,即EE(15-4)i=NA式中I为截面的最小形心主轴惯性矩,A为截面面积。柔度元又称为压杆的长细比。它全面的反映了压杆长度、约束条件、截面尺寸和形状对临界力的影响。柔度入在稳定计算中是个非常重要的量,根据入所处的范围,可以把压杆分为三类:(1)细长杆(≥)当临界应力小于或等于材料的比例极限,时,即元ECar≤aA压杆发生弹性失稳。若令E(15-5)p=op则入≥入,时,压杆发生弹性失稳。这类压杆又称为大柔度杆。对于不同的材料,因弹性模量E和比例极限α,各不相同,入,的数值亦不相同。例如A3钢,E=210GPa,,=200MPa,用式(15-5)可算得入,=102。(2)中长杆(≤≤)这类杆又称中柔度杆。这类压杆失稳时,横截面上的应力已超过比例极限,故属于弹塑性稳定问题。对于中长杆,一般采用经验公式计算其临界应力,如直线公式:o.=a-ba(15-6)
材 料 力 学 教 案 §9-4 欧拉公式的适用范围 如上节所述,欧拉公式只有在弹性范围内才是适用的。为了判断压杆失稳时是否处于弹 性范围,以及超出弹性范围后临界力的计算问题,必须引入临界应力及柔度的概念。 压杆在临界力作用下,其在直线平衡位置时横截面上的应力称为临界应力,用 cr 表示。 压杆在弹性范围内失稳时,则临界应力为: 2 2 2 2 2 2 2 ( ) ( ) E l Ei l A EI A Pcr cr = = = = (15-3) 式中 称为柔度, i 为截面的惯性半径,即 i l = , A I i = (15-4) 式中I为截面的最小形心主轴惯性矩,A为截面面积。 柔度 又称为压杆的长细比。它全面的反映了压杆长度、约束条件、截面尺寸和形状 对临界力的影响。柔度 在稳定计算中是个非常重要的量,根据 所处的范围,可以把压 杆分为三类: (1)细长杆( p ) 当临界应力小于或等于材料的比例极限 p 时,即 cr p E = 2 2 压杆发生弹性失稳。若令 p p E 2 = (15-5) 则 p 时,压杆发生弹性失稳。这类压杆又称为大柔度杆。对于不同的材料,因弹性模量 E和比例极限 p 各不相同, p 的数值亦不相同。例如 A3 钢, E = 210GPa , = 200MPa p ,用式(15-5)可算得 p = 102 。 (2)中长杆( s p ) 这类杆又称中柔度杆。这类压杆失稳时,横截面上的应力已超过比例极限,故属于弹塑 性稳定问题。对于中长杆,一般采用经验公式计算其临界应力,如直线公式: cr = a − b (15-6)
+七讲式中a、b为与材料性能有关的常数。当c。=c,时,其相应的柔度2,为中长杆柔度的下限,据式(15-6)不难求得:A=a-o.例如A3钢,,=235MPa,a=304MPa,b=1.12MPa,代入上式算得入,=61.6。(3)粗短杆(≤)这类杆又称为小柔度杆。这类压杆将发生强度失效,而不是失稳。故0.=0,Ccl9=0上述三类压杆临界应力与元的关系,可画出OECr=a-baC。-元曲线如图15-7所示。该图称为压杆的临界应Of力图。Gr=年5需要指出的是,对于中长杆和粗短杆,不同的工程设计中,可能采用不同的经验公式计算临界应力,如抛物线公式=α -b,(α, 和b, 也是和材料有关的常数)等,请读者注意查阅相关的设计规范。图15-1压杆的临界应力图常用材料的a、b和~值表9-1材料pa(MPa)b(MPa)3041.12102A3钢,=235MPa4612.56895优质碳钢,=306MPa332.21.4540铸铁木材28.70.190
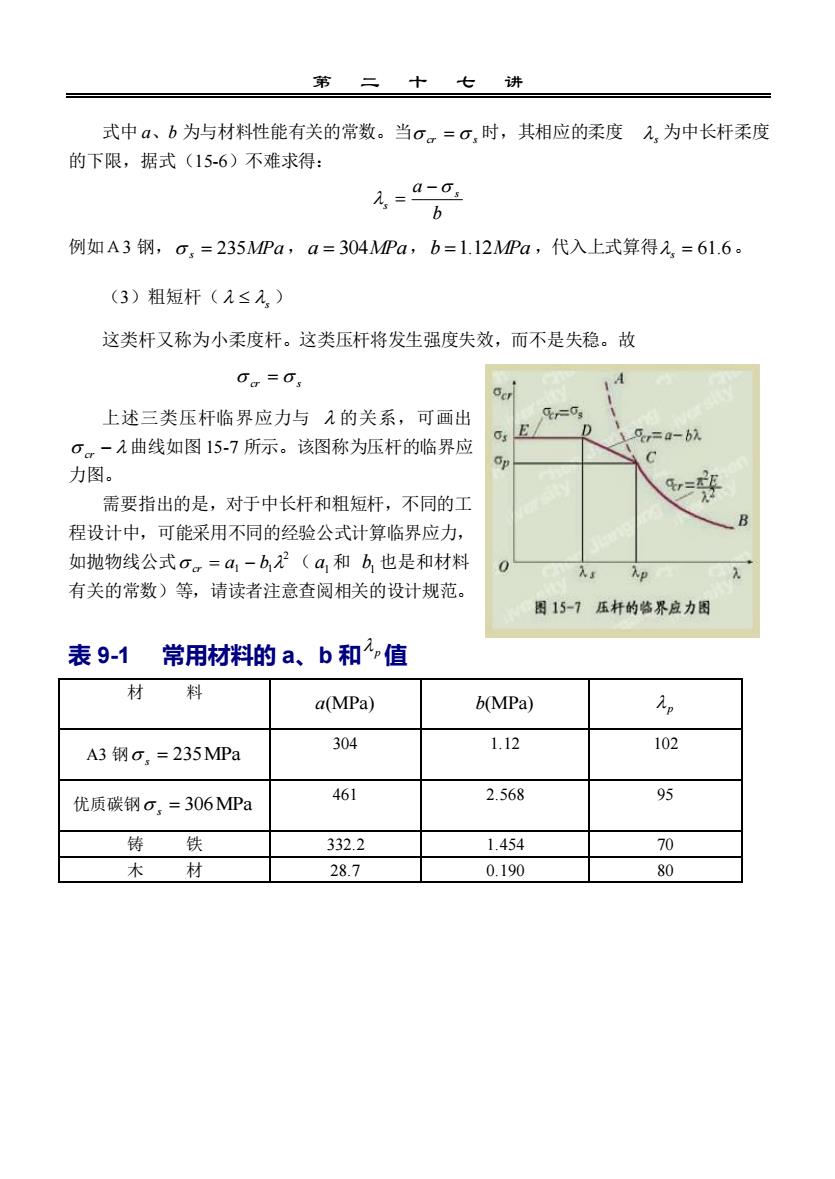
第 二 十 七 讲 式中 a、b 为与材料性能有关的常数。当 cr = s 时,其相应的柔度 s 为中长杆柔度 的下限,据式(15-6)不难求得: b a s s − = 例如A3 钢, s = 235MPa,a = 304MPa,b =1.12MPa ,代入上式算得 s = 61.6。 (3)粗短杆( s ) 这类杆又称为小柔度杆。这类压杆将发生强度失效,而不是失稳。故 cr = s 上述三类压杆临界应力与 的关系,可画出 cr − 曲线如图 15-7 所示。该图称为压杆的临界应 力图。 需要指出的是,对于中长杆和粗短杆,不同的工 程设计中,可能采用不同的经验公式计算临界应力, 如抛物线公式 2 cr = a1 − b1 ( 1 a 和 1 b 也是和材料 有关的常数)等,请读者注意查阅相关的设计规范。 表 9-1 常用材料的 a、b 和 p 值 材 料 a(MPa) b(MPa) p A3 钢 = 235MPa s 304 1.12 102 优质碳钢 = 306MPa s 461 2.568 95 铸 铁 332.2 1.454 70 木 材 28.7 0.190 80

材料力学教案S9-5压杆的稳定计算工程上通常采用下列两种方法进行压杆的稳定计算。1.安全系数法为了保证压杆不失稳,并具有一定的安全裕度,因此压杆的稳定条件可表示为(15-7)n-≥n式中P为压杆的工作载荷,P。是压杆的临界载荷,n,是稳定安全系数。由于压杆存在初曲率和载荷偏心等不利因素的影响。n,值一般比强度安全系数要大些,并且入越大,n,值也越大。具体取值可从有关设计手册中查到。在机械、动力、冶金等工业部门,由于载荷情况复杂,一般都采用安全系数法进行稳定计算。2.稳定系数法压杆的稳定条件有时用应力的形式表达为α-P≤[0].(15-8)A,它总式中的P为压杆的工作载荷,A为横截面面积,[o],为稳定许用应力。[o],=nst是小于强度许用应力[0]。于是式(15-8)又可表达为Pa:≤0[0](15-9)A其中β称为稳定系数,它由下式确定:[o]_.n_a.n<1@:[o]o式中α,为强度计算中的危险应力,由临界应力图(图15-7)可看出,。<α,且n<nst故β为小于1的系数,也是柔度的函数。表92所列为几种常用工程材料的-对应数值。对于柔度为表中两相邻入值之间的β,可由直线内插法求得。由于考虑了杆件的初曲率和载荷偏心的影响,即使对于粗短杆,仍应在许用应力中考虑稳定系数。在土建工程中,一般按稳定系数法进行稳定计算还应指出,在压杆计算中,有时会遇到压杆局部有截面被削弱的情况,如杆上有开孔、切糟等。由于压杆的临界载荷是从研究整个压杆的弯曲变形来决定的,局部截面的削弱对整体变形影响较小,故稳定计算中仍用原有的截面几何量。但强度计算是根据危险点的应力进行的,故必须对削弱了的截面进行强度校核,即
材 料 力 学 教 案 §9-5 压杆的稳定计算 工程上通常采用下列两种方法进行压杆的稳定计算。 1.安全系数法 为了保证压杆不失稳,并具有一定的安全裕度,因此压杆的稳定条件可表示为 st cr n P P n = (15-7) 式中 P 为压杆的工作载荷, Pcr 是压杆的临界载荷, st n 是稳定安全系数。由于压杆存在初曲 率和载荷偏心等不利因素的影响。 st n 值一般比强度安全系数要大些,并且 越大, st n 值也 越大。具体取值可从有关设计手册中查到。在机械、动力、冶金等工业部门,由于载荷情况 复杂,一般都采用安全系数法进行稳定计算。 2.稳定系数法 压杆的稳定条件有时用应力的形式表达为 st A P = [ ] (15-8) 式中的 P 为压杆的工作载荷, A 为横截面面积, st [] 为稳定许用应力。 st cr st n [] = ,它总 是小于强度许用应力 [ ] 。于是式(15-8)又可表达为 = [ ] A P (15-9) 其中 称为稳定系数,它由下式确定: 1 [ ] [ ] = = = u st cr st u st cr n n n n 式中 u 为强度计算中的危险应力,由临界应力图(图 15-7)可看出, cr u ,且 n nst , 故 为小于 1 的系数, 也是柔度 的函数。表 9.2 所列为几种常用工程材料的 − 对应 数值。对于柔度为表中两相邻 值之间的 ,可由直线内插法求得。由于考虑了杆件的初 曲率和载荷偏心的影响,即使对于粗短杆,仍应在许用应力中考虑稳定系数 。在土建工程 中,一般按稳定系数法进行稳定计算。 还应指出,在压杆计算中,有时会遇到压杆局部有截面被削弱的情况,如杆上有开孔、 切糟等。由于压杆的临界载荷是从研究整个压杆的弯曲变形来决定的,局部截面的削弱对整 体变形影响较小,故稳定计算中仍用原有的截面几何量。但强度计算是根据危险点的应力进 行的,故必须对削弱了的截面进行强度校核,即