中国地质大学（武汉）：《数字信号处理》课程教学资源（课件讲稿）第五章 数字滤波器的基本结构

3、级联型 将系统函数按零极点因式分解： M M M bz 4-pz1-921-9ie') k=0 二A k=1 N, N 1-∑az* Π1-c2)Π(1-dz11-de) k=1 k=] k=1 为常数 M=M1+2M2 P,和c分别为实数零、极点 N=N,+2N2 9k,9和dk,d分别为复共轭零、极点

3、级联型 将系统函数按零极点因式分解: 1 2 1 2 1 1 * 1 0 1 1 1 1 * 1 1 1 1 (1 ) (1 )(1 ) ( ) 1 (1 ) (1 )(1 ) M M M k k k k k k k k N N N k k k k k k k k b z p z q z q z H z A a z c z d z d z                              A为常数* * , , q q d d k k k k 和 分别为复共轭零、极点 p c k k 和 分别为实数零、极点 M M M  1 2 2 N N N  1 2 2

将共轭成对的复数组合成二阶多项式，系数即为实数。 为采用相同结构的子网络，也将两个实零点/极点组合成二 阶多项式 24回 当w黄，共[节 当零点为奇数时： 有一个B2k=0 12 当极点为奇数时： 有一个x2k=0 图5-7级联结构的一阶基本节和二阶基本节结构

将共轭成对的复数组合成二阶多项式，系数即为实数。 为采用相同结构的子网络，也将两个实零点/极点组合成二 阶多项式 1 2 1 2 1 2 1 2 1 ( ) ( ) 1 k k k k k k k z z H z A A H z z z                 2 0  k  当零点为奇数时： 有一个 2 0  k  当极点为奇数时： 有一个 1 2 N M N         当 时，共有 节

e8之 H( B2() 图5-8级联结构(M=N)

1 2 1 2 1 2 1 2 1 ( ) ( ) 1 k k k k k k k z z H z A A H z z z                

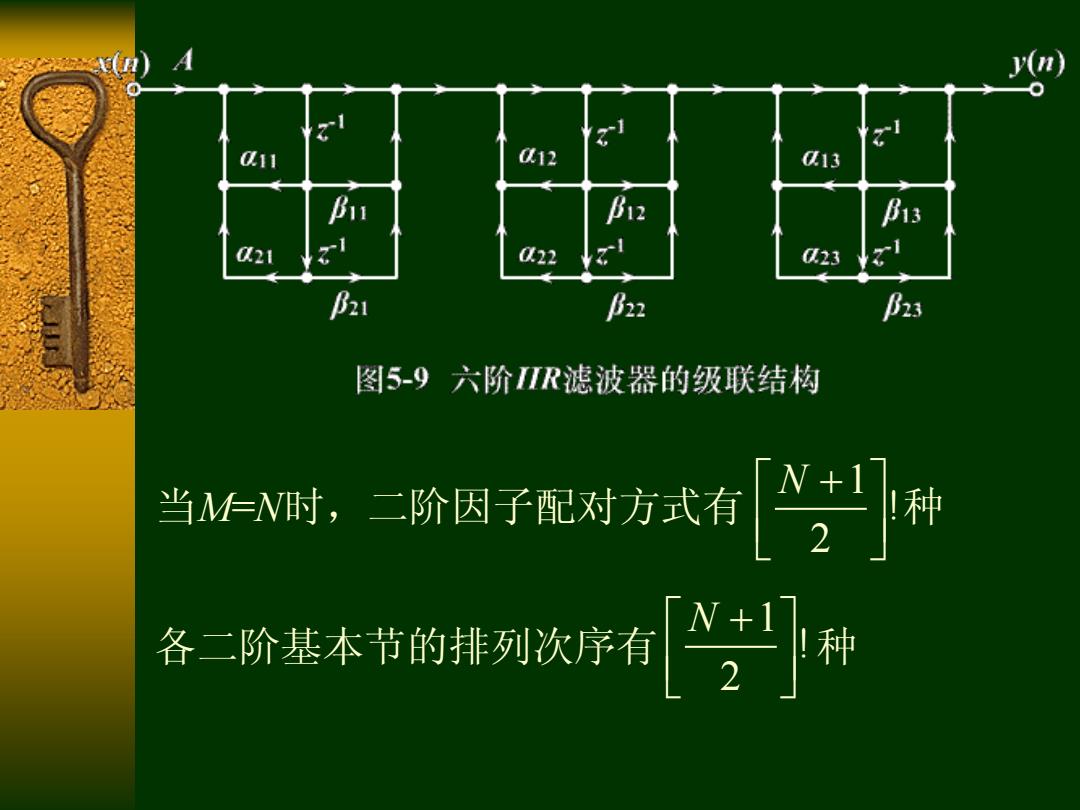
A 012 013 B12 1 21 022 023 B21 B22 图5-9六阶IR滤波器的级联结构 当MN时，二阶因子配对方式 [} 各二阶基本节的排列次序有

1 ! 2   N      各二阶基本节的排列次序有 种 1 ! 2   N      当M=N时，二阶因子配对方式有 种

级联型的特点： 调整系数Bk,B,能单独调整滤波器的第对零点， 而不影响其它零极点 调整系数Ck,2能单独调整滤波器的第k对极点， 而不影响其它零极点 便于调整滤波器频率响应性能 ◆运算的累积误差较小 ◆具有最少的存储器

级联型的特点：  调整系数 ， 能单独调整滤波器的第k对零点， 而不影响其它零极点 1k  2k  运算的累积误差较小  具有最少的存储器 便于调整滤波器频率响应性能 调整系数 1k ，  2k 能单独调整滤波器的第k对极点， 而不影响其它零极点