
例1:判断下图中各支路集合是否是图G的割集? 0. (a,d,f)是 (a,b,c,d)是 (a,b,c,d,e)不是 特点:①全移,G一分为二②少移一条,G连通
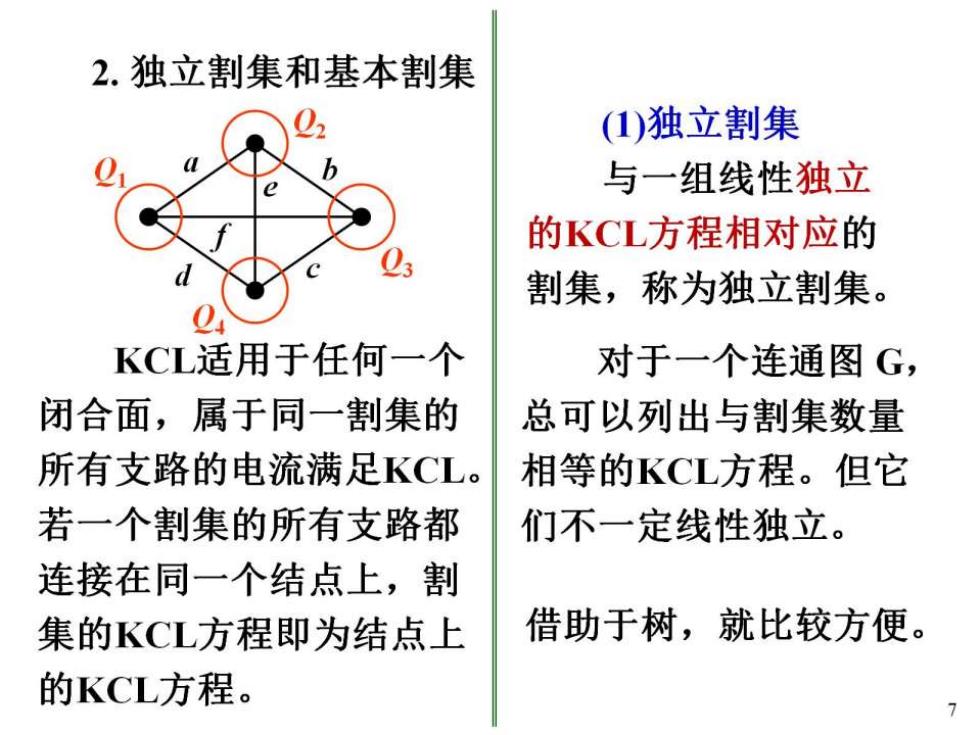
2.独立割集和基本割集 ()独立割集 与一组线性独立 的KCL方程相对应的 割集,称为独立割集。 KCL适用于任何一个 对于一个连通图G, 闭合面,属于同一割集的 总可以列出与割集数量 所有支路的电流满足KCL。 相等的KCL方程。但它 若一个割集的所有支路都 们不一定线性独立。 连接在同一个结点上,割 集的KCL方程即为结点上 借助于树,就比较方便。 的KCL方程
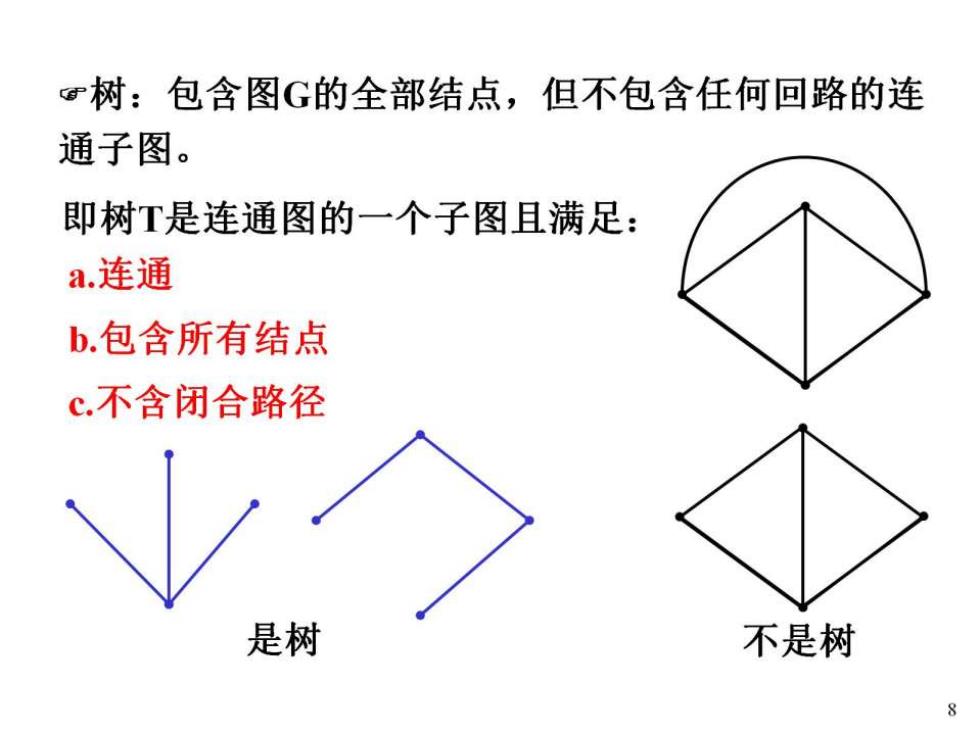
树:包含图G的全部结点,但不包含任何回路的连 通子图。 即树T是连通图的一个子图且满足: a.连通 b.包含所有结点 c.不含闭合路径 是树 不是树 8
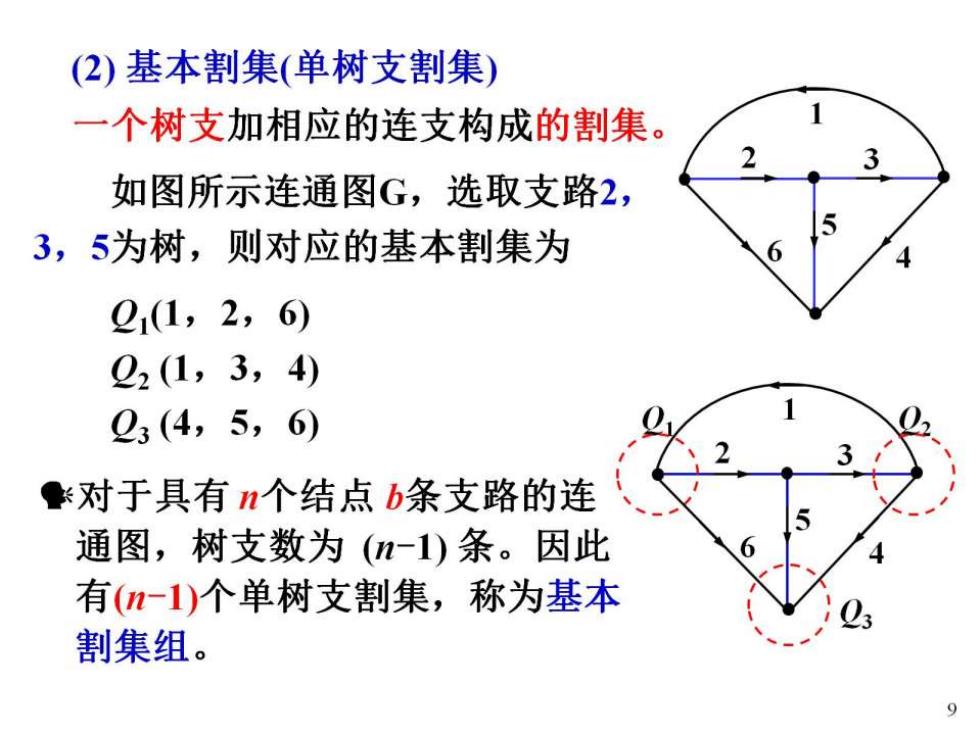
(2)基本割集(单树支割集) 一个树支加相应的连支构成的割集。 如图所示连通图G,选取支路2, 3,5为树,则对应的基本割集为 21(1,2,6) 22(1,3,4) 23(4,5,6) ●对于具有n个结点b条支路的连 通图,树支数为(-1)条。因此 有(-1)个单树支割集,称为基本 割集组
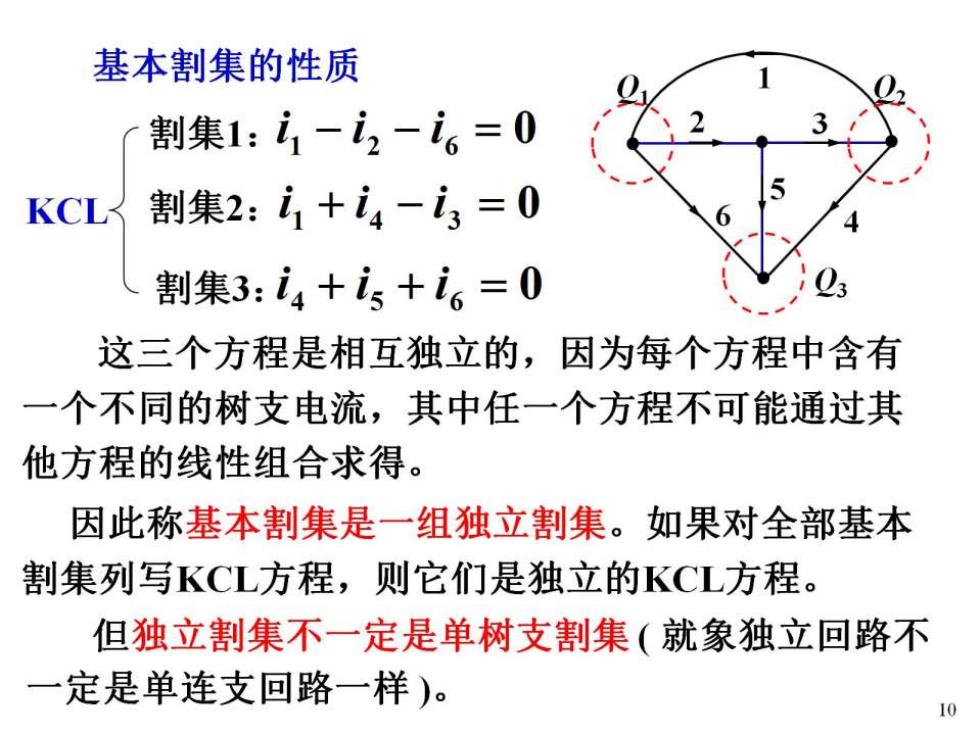
基本割集的性质 割集1:i1-i2-6=0 KCL割集2:i1+i4-i3=0 割集3:i4+is+i6=0 这三个方程是相互独立的,因为每个方程中含有 一个不同的树支电流,其中任一个方程不可能通过其 他方程的线性组合求得。 因此称基本割集是一组独立割集。如果对全部基本 割集列写KCL方程,则它们是独立的KCL方程。 但独立割集不一定是单树支割集(就象独立回路不 一定是单连支回路一样)。 10