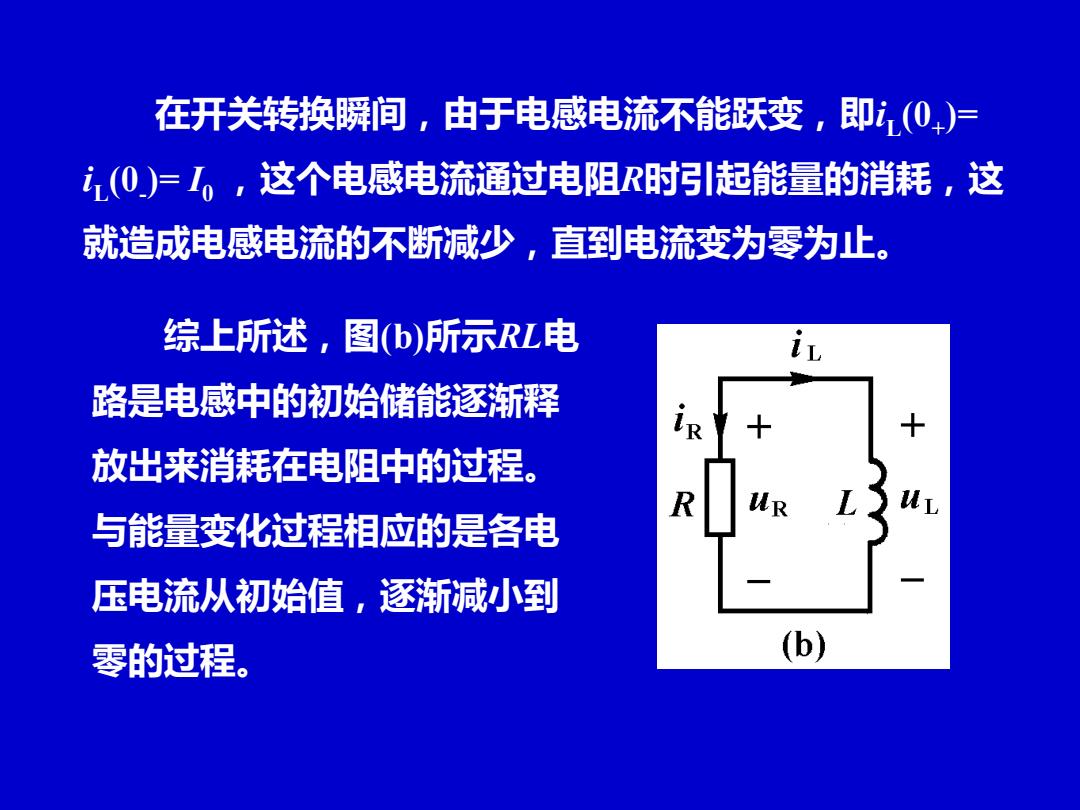
在开关转换瞬间,由于电感电流不能跃变,即(0)尸 i(0)=1,,这个电感电流通过电阻R时引起能量的消耗,这 就造成电感电流的不断减少,直到电流变为零为止。 综上所述,图b)所示RL电 路是电感中的初始储能逐渐释 十 放出来消耗在电阻中的过程。 R 与能量变化过程相应的是各电 压电流从初始值,逐渐减小到 零的过程。 (b)
在开关转换瞬间,由于电感电流不能跃变,即iL (0+ )= iL (0- )= I0 ,这个电感电流通过电阻R时引起能量的消耗,这 就造成电感电流的不断减少,直到电流变为零为止。 综上所述,图(b)所示RL电 路是电感中的初始储能逐渐释 放出来消耗在电阻中的过程。 与能量变化过程相应的是各电 压电流从初始值,逐渐减小到 零的过程
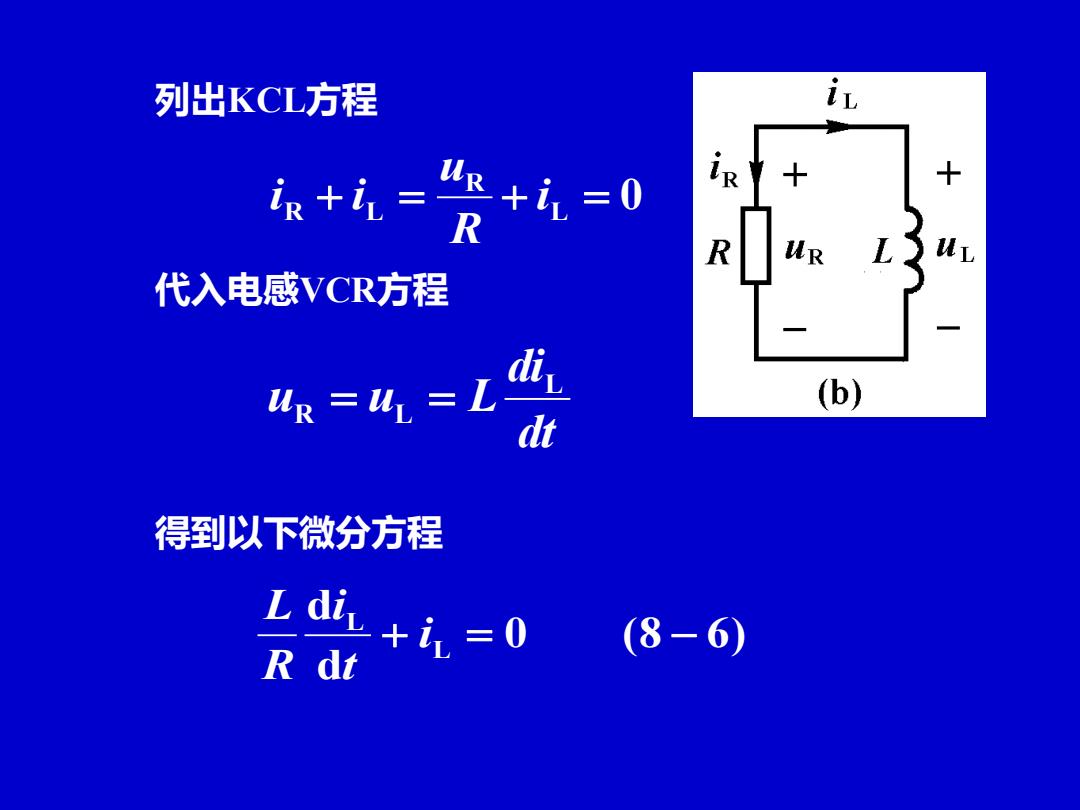
列出KCL方程 丝+=袋+元=0 R R us 代入电感VCR方程 =h=L (b) dt 得到以下微分方程 L di+i= (8-6) R dt
列出KCL方程 L 0 R R + L = + i = R u i i 代入电感VCR方程 dt di u u L L R = L = 得到以下微分方程 0 (8 6) d d L L + i = − t i R L

这个微分方程与式(8-1)相似,其通解为 )=e空 (t≥0) 代入初始条件(0)=I求得 K=Io 最后得到电感电流和电感电压的表达式为 ()=1e艺=1,e (t20) (8-7a) 0=l=-e立-Re (t>0) (8-7b)
这个微分方程与式(8-1)相似,其通解为 ( ) e ( 0) L = − i t K t t L R 代入初始条件iL (0+ )=I0求得 0 K = I 最后得到电感电流和电感电压的表达式为 ( 0) (8 7b) d d ( ) ( ) e e ( 0) (8 7a) 0 0 L L L 0 0 = = − = − − = = − − − − − RI e RI e t t i u t L i t I I t t t L R t t L R τ τ
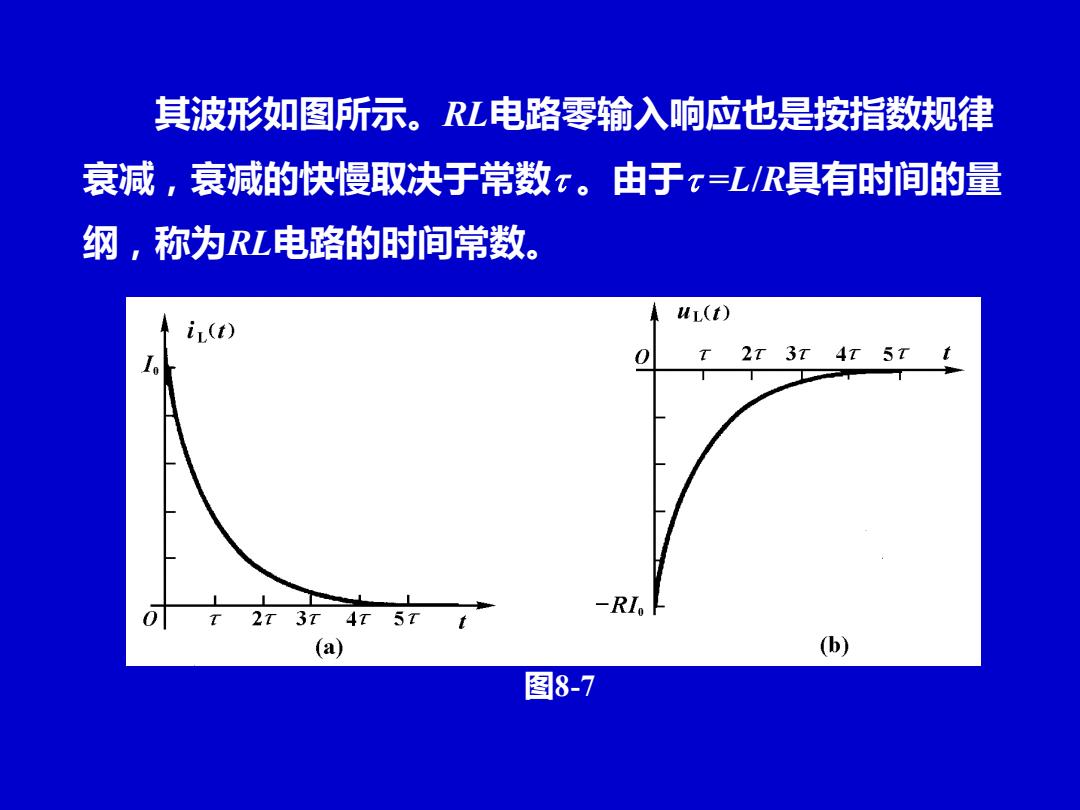
其波形如图所示。L电路零输入响应也是按指数规律 衰减,衰减的快慢取决于常数x。由于x=L/R具有时间的量 纲,称为RL电路的时间常数。 HL() iL(t) T 2T 3T 4t 5t t 0 T 2T 3t 4t 5T t -RIo (a) (b) 图8-7
其波形如图所示。RL电路零输入响应也是按指数规律 衰减,衰减的快慢取决于常数 。由于 =L/R具有时间的量 纲,称为RL电路的时间常数。 图8-7
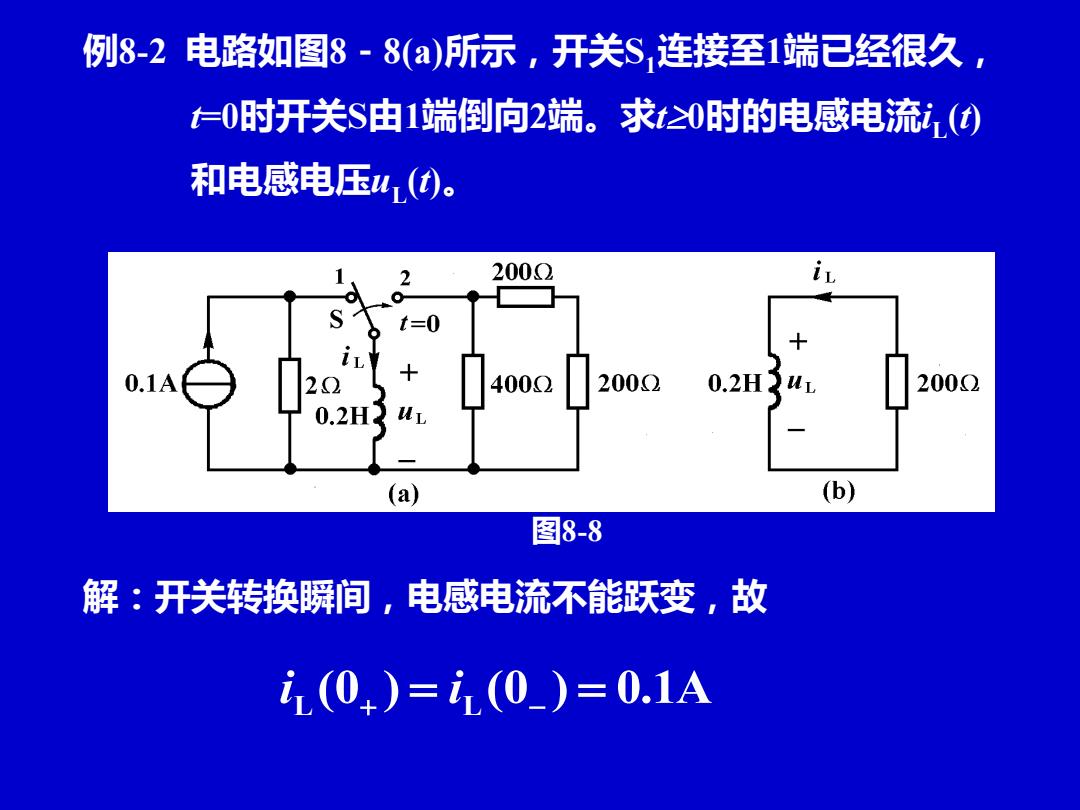
例8-2电路如图8-8(a)所示,开关S,连接至1端已经很久, t=0时开关S由1端倒向2端。求t≥0时的电感电流1() 和电感电压4()。 1 2 2002 it t=0 0.1 400Q2 2002 2002 0.2H3 (a) (b) 图8-8 解:开关转换瞬间,电感电流不能跃变,故 i(0+)=(0_)=0.1A
例8-2 电路如图8-8(a)所示,开关S1连接至1端已经很久, t=0时开关S由1端倒向2端。求t0时的电感电流iL (t) 和电感电压uL (t)。 图8-8 解:开关转换瞬间,电感电流不能跃变,故 i L (0+ ) = i L (0− ) = 0.1A