
第七章电容元件和电感元件 前几章讨论了电阻电路,即由独立电源和电阻、受控 源、理想变压器等电阻元件构成的电路。 描述这类电路电 压电流约束关系的电路方程是代数方程。但在实际电路的 分析中,往往还需要采用电容元件和电感元件去建立电路 模型。这些元件的电压电流关系涉及到电压电流对时间的 微分或积分,称为动态元件。含动态元件的电路称为动态 电路,描述动态电路的方程是微分方程。本章先介绍两种 储能元件一电容元件和电感元件。再介绍简单动态电路微 分方程的建立。以后两章讨论一阶电路和二阶电路的时域 分析,最后一章讨论线性时不变动态电路的频域分析
第七章 电容元件和电感元件 前几章讨论了电阻电路,即由独立电源和电阻、受控 源、理想变压器等电阻元件构成的电路。描述这类电路电 压电流约束关系的电路方程是代数方程。但在实际电路的 分析中,往往还需要采用电容元件和电感元件去建立电路 模型。这些元件的电压电流关系涉及到电压电流对时间的 微分或积分,称为动态元件。含动态元件的电路称为动态 电路,描述动态电路的方程是微分方程。本章先介绍两种 储能元件—电容元件和电感元件。再介绍简单动态电路微 分方程的建立。以后两章讨论一阶电路和二阶电路的时域 分析,最后一章讨论线性时不变动态电路的频域分析

常用的几种电容器 16V470HP 马 C10 RC8 CD26-B2 260y11.12 16V000F 的只
常用的几种电容器
§7-1电容元件 一、电容元件 集总参数电路中与电场有关的物理过程集中在电容元件 中进行,电容元件是构成各种电容器的电路模型所必需的 一种理想电路元件。 电容元件的定义是:如果一个二端元件在任一时刻,其 电荷与电压之间的关系由-q平面上一条曲线所确定,则称 此二端元件为电容元件。 (a (b) (d) 图7-1
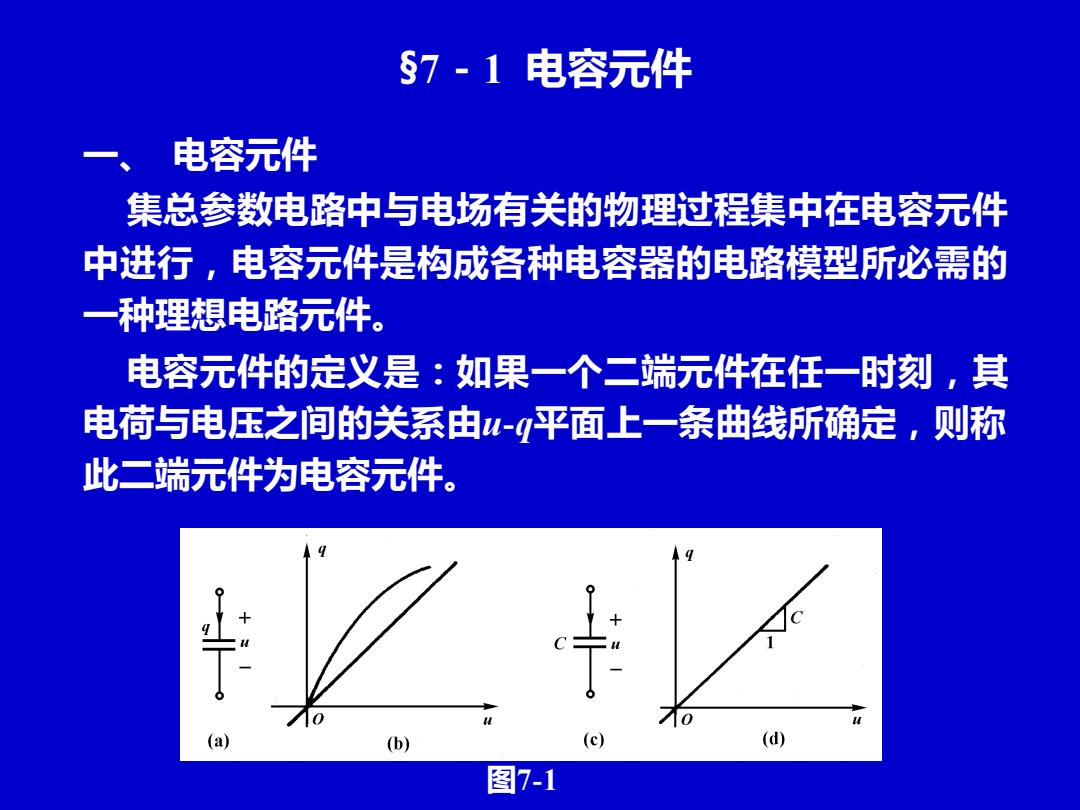
§7-1 电容元件 一、 电容元件 集总参数电路中与电场有关的物理过程集中在电容元件 中进行,电容元件是构成各种电容器的电路模型所必需的 一种理想电路元件。 电容元件的定义是:如果一个二端元件在任一时刻,其 电荷与电压之间的关系由u-q平面上一条曲线所确定,则称 此二端元件为电容元件。 图7-1

电容元件的符号和特性曲线如图7-1(a)和(b)所示。 (d) 图7-1 (a)电容元件的符号 (©)线性时不变电容元件的符号 b)电容元件的特性曲线 (d)线性时不变电容元件的特性曲线 其特性曲线是通过坐标原点一条直线的电容元件称为 线性电容元件,否则称为非线性电容元件
(a) 电容元件的符号 (c) 线性时不变电容元件的符号 (b) 电容元件的特性曲线 (d) 线性时不变电容元件的特性曲线 电容元件的符号和特性曲线如图7-1(a)和(b)所示。 其特性曲线是通过坐标原点一条直线的电容元件称为 线性电容元件,否则称为非线性电容元件。 图7-1

(b (c (d) 图7-1 线性时不变电容元件的符号与特性曲线如图(c)和(d)所 示,它的特性曲线是一条通过原点不随时间变化的直线 其数学表达式为 q Cu (7-1) 式中的系数C为常量,与直线的斜率成正比,称为电 容,单位是法拉],用F表示
线性时不变电容元件的符号与特性曲线如图(c)和(d)所 示,它的特性曲线是一条通过原点不随时间变化的直线, 其数学表达式为 q = Cu (7 −1) 式中的系数C为常量,与直线的斜率成正比,称为电 容,单位是法[拉],用F表示。 图7-1