
第九章二阶电路分析 由二阶微分方程描述的电路称为二阶电路。 分析二阶电路的方法仍然是建立二阶微分方程 并利用初始条件求解得到电路的响应。本章主要 讨论含两个动态元件的线性二阶电路,重点是讨 论电路的零输入响应。最后介绍如何利用计算机 程序分析高阶动态电路
第九章 二阶电路分析 由二阶微分方程描述的电路称为二阶电路。 分析二阶电路的方法仍然是建立二阶微分方程, 并利用初始条件求解得到电路的响应。本章主要 讨论含两个动态元件的线性二阶电路,重点是讨 论电路的零输入响应。最后介绍如何利用计算机 程序分析高阶动态电路
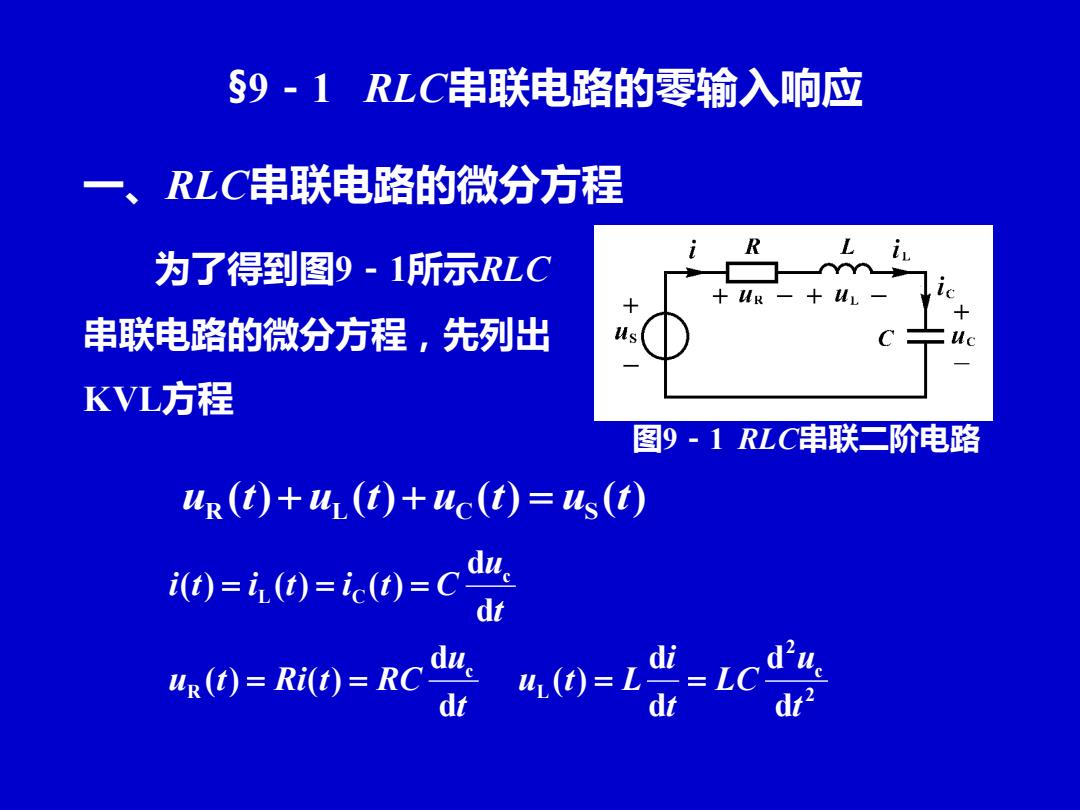
§9-1RLC串联电路的零输入响应 一、RLC串联电路的微分方程 为了得到图9-1所示RLC L i Y +u ic 串联电路的微分方程,先列出 KVL方程 图9-1RLC串联二阶电路 ur (t)+ur (t)+uc(t)us (t) 0=0=0=c出 ()R)=RC dt?
§9-1 RLC串联电路的零输入响应 一、RLC串联电路的微分方程 图9-1 RLC串联二阶电路 ( ) ( ) ( ) ( ) R L C S u t + u t + u t = u t 2 c 2 L c R c L C d d d d ( ) d d ( ) ( ) d d ( ) ( ) ( ) t u LC t i u t L t u u t Ri t RC t u i t i t i t C = = = = = = = 为了得到图9-1所示RLC 串联电路的微分方程,先列出 KVL方程

根据前述方程得到以下微分方程 LC+RC +e=(0 (9-1) dt 这是一个常系数非齐次线性二阶微分方程。 零输入响应方程为 dt2 (9-2) dt 其特征方程为 LCs2+RCs+1=0 (9-3) 其特征根为 S2=-2 (9-4)
根据前述方程得到以下微分方程 ( ) (9 1) d d d d C S C 2 C 2 + + u = u t − t u RC t u LC 这是一个常系数非齐次线性二阶微分方程。 0 (9 2) d d d d C C 2 C 2 + + u = − t u RC t u LC 其特征方程为 1 0 (9 3) 2 LCs + RCs+ = − 其特征根为 (9 4) 1 2 2 2 1 2 − − = − L LC R L R s , 零输入响应方程为

电路微分方程的特征根,称为电路的固有频率。当R, L,C的量值不同时,特征根可能出现以下三种情况 1R>2片时,Sp心,为不相等的实根。过阻尼简况。 2,R=2怎时,,小,为两个相等的实根。 临界阻尼 情况。 3.R<3亿时,1心,为共轭复数限。 欠阻尼情况
电路微分方程的特征根,称为电路的固有频率。当R, L,C的量值不同时,特征根可能出现以下三种情况 1. 时, 为不相等的实根。过阻尼情况。 C L R 2 1 2 s ,s 2. 时, 为两个相等的实根。临界阻尼 情况。 1 2 s ,s C L R = 2 3. 时, 为共轭复数根。欠阻尼情况。 C L R 2 1 2 s ,s

二、过阻尼情况 当R>2 时,电路的固有频率,,S,为两个不相同的 实数,齐次微分方程的解答具有下面的形式 uc(t)=Kje+Ke (9-5) 式中的两个常数K,,K,由初始条件(0)和4.(0)确定。 uc(0)=K1+K2 (9-6) 对式9-5)求导,再令0得到 diuc(s= (9-7) dt
二、过阻尼情况 当 时,电路的固有频率s1,s2为两个不相同的 实数,齐次微分方程的解答具有下面的形式 C L R 2 ( ) e e (9 5) 1 2 C = 1 + 2 − s t s t u t K K 式中的两个常数K1,K2由初始条件iL (0)和uc (0) 确定。 (0) (9 6) uC = K1 + K2 − 对式(9-5)求导,再令t=0得到 (9 7) (0) d d ( ) L 0 1 1 2 2 C = = + = − C i K s K s t u t t