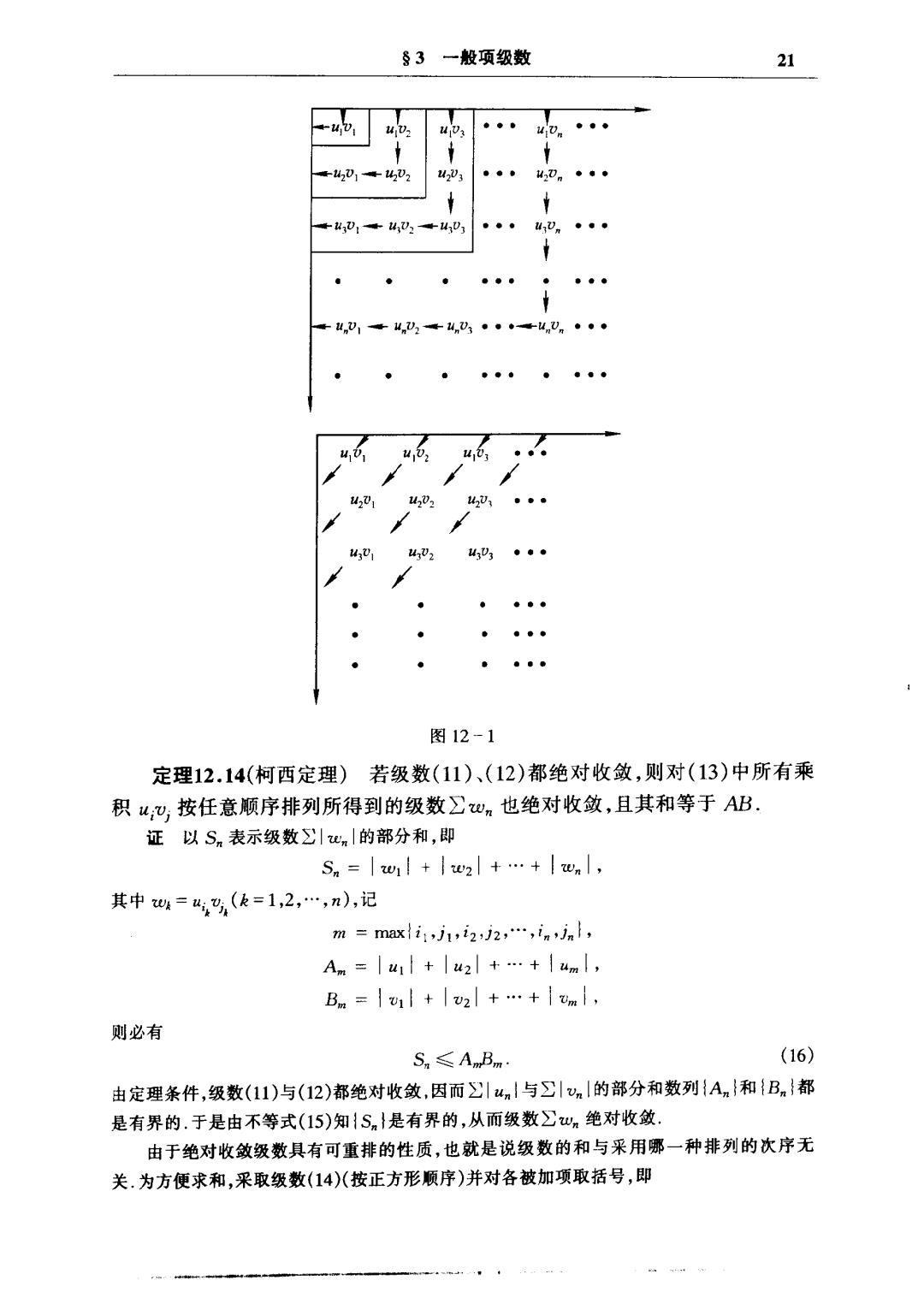
§3一般项级数 21 403 403 ●●● 4:0n .. 4201402 423 ●●● 20n。。· 3D1+4U3+403 ·●·4Vn。·● tu1+n24n03··◆uVn··· ● 自● 图12-1 定理12.14(柯西定理)若级数(11)、(12)都绝对收敛,则对(13)中所有乘 积u℃按任意顺序排列所得到的级数∑n也绝对收敛,且其和等于AB. 证以Sn表示级数引n|的部分和,即 Sn=w1+2+…+|wn, 其中w=4(k=1,2,…,n),记 m maxli,j,i,j2,,in,n, Am=|u1+|u2+…+4m|, Bm=|1l+|v2|+…+m, 则必有 Sn≤AmBm (16) 由定理条件,级数(11)与(12)都绝对收敛,因而∑un与∑引vnI的部分和数列{An}和{Bn}都 是有界的.于是由不等式(15)知{Sn}是有界的,从而级数∑wn绝对收敛。 由于绝对收敛级数具有可重排的性质,也就是说级数的和与采用哪一种排列的次序无 关.为方便求和,采取级数(14)(按正方形顺序)并对各被加项取括号,即

22 第十二章数项级数 u1v1+(u12+u22+u2v1)+(u13+42℃3+u3v3+u3v2+u3v1)+…, 把每一括号作为一项,得新级数 p1+p2+p3+…+pn+…, (17) 它与级数∑wn同时收敛,且和数相同.现以P.表示级数(17)的部分和,它与级数(11),(12) 的部分和A,与Bn有如下关系式: Pn=ABn、 从而有 lim P=lim A,B.lim A.lim B,=AB 0 例2 等比级数 =1+r+2+…++…,1r1<1 1-r 是绝对收敛的.将(∑")2按(15)的顺序排列,则得到 (1-72=1+(,+)+(r2+2+2+…+(+…+)+… 1 n+1个 =1+2x+3r2+…+(n+1)rn+… 0 三阿贝耳判别法和狄利克雷判别法 本段介绍两个判别一般项级数收敛性的方法,先引进一个公式: 引理(分部求和公式,也称阿贝耳变换)设e:,v,(i=1,2,…,n)为两组实 数,若令 0=1+2+…+Vg (k=1,2,,n), 则有如下分部求和公式成立: 2e4=(e1-e2)a1+(e2-e32+…+(e-1-En)加-1+e0a.(18) 证以1=01,℃%=0g-0%-1(k=2,3,…,n)分别乘以e(k=1,2,…,n), 整理后就得所要证的公式(18). 0 推论(阿贝耳引理)若 (i)e1,e2,…,en是单调数组; (ii)对任一正整数k(1≤k≤n)有o|≤A(这里o。=1+…+%),则记 e=max{|ek}时,有 (19) 证由()知道 E1-E2,E2-83,.,En-1-En 都是同号的.于是由分部求和公式及条件()推得 2=l(e1-ea+(e,-o++(1e,.1+e

§3一般项级数 23 ≤A|(e1-e2)+(e2-e3)+…+(em-1-en)l+A ler l =Ale-E+A le ≤A(|e1l+2lenI) ≤3EA. 0 现在讨论级数 anbn=a1b1+a2b2t…+abn+… (20) 收敛性的判别法, 定理12.15(阿贝耳判别法)若{an|为单调有界数列,且级数∑bn收敛, 则级数(20)收敛 证由级数∑bn收敛,依柯西准则,对任给正数e,存在正数N,使当n>N 时对任一正整数p,都有 o.<c. 又由于数列{an}有界,所以存在M>0,使1an≤M,应用(19)式结果可得 到 ≤3Me 这就说明级数(20)收敛 0 定理12.16(狄利克雷判别法)若数列{an}单调递减,且liman=0,又级数 ∑bn的部分和数列有界,则级数(20)收敛 证明方法类似于定理12.15,请读者自证. 由阿贝耳判别法知道,若级数∑山n收敛,则下述两个级数: (>0, n+1 都收敛 例3若数列{an}具有性质: a1≥a2≥…≥an≥…,liman=0, 则级数∑ansin nx和∑an cos nx对任何x∈(0,2π)都收敛. 解因为 2sin(}+sc)=sm受+(sn2x-sin受+… +[smn+2)x-simn-}z]

24 第十二章数项级数 =sin+)z, 当x∈(0,2m)时,sin乏≠0,故得到 +之s红 3=1 2sin号 (21) 所以级数》∑cos nx的部分和数列当x∈(0,2π)时有界,由狄利克雷判别法推得 级数∑an cos nx收敛.同理可证级数∑ansin nx也是收敛的. 0 作为例3的特殊情形,我们知道级数 ∑sinz 和 ∑cos n n 对一切x∈(0,2π)都收敛 习 题 1.下列级数哪些是绝对收敛,条件收敛或发散的: (1)n严; n! (2)2(-1)”n+ (3)-1) (4)2(-10sm品: 6+): (6)3-1)m(n+12. n+1 ()8(-1(29)八; 8)2!(月 2.应用阿贝耳判别法或狄利克雷判别法判断下列级数的收敛性: (1)-12x n 1+x" (x>0): (2)sin匹,x∈(0,2x)(a>0); (3)2(-1)nosn匹】 3.设an>0,an>a+1(n=1,2,…)且liman=0.证明级数 (-1)n-101+a2++a n 是收敛的, 4.设pn,9n如(8)式所定义.证明:若∑un条件收敛,则级数∑pn与∑qm都是发散的. 5.写出下列级数的乘积:

总练习题 25 )(2x(2(-1)m):2)(() 6,注明级数宫品与会篇笔对收效,鼠它们的乘积等于宫a片 n! 7.重排级数(-1)n+11,使它成为发散级数。 8.证明:级数-1) 一一收敛 n 总练习题 1.证明:若正项级数∑un收敛,且数列{un}单调,则lim nun=0, 2.若级数∑an与∑cn都收敛,且成立不等式 an≤bn≤cn(n=1,2,…), 证明级数∑bn也收敛.若∑an,∑cn都发散,试问bn一定发散吗? 3.若m公=0,且级数0,绝对收敛,证明级数公,也收敛若上述条件中只知道 bn收敛,能推得∑an收敛吗? 4.(1)设un为正项级数,且“n+1<1,能否断定》un收敛? 2)对于级数.有 n+l ≥1,能否断定级数un不绝对收敛,但可能条件收敛? un (3)设∑un为收敛的正项级数,能否存在一个正数e,使得 =c0. lim 1 5.证明:若级数》an收敛,(bn+1-bn)绝对收敛,则级数abn也收敛。 6.设an>0,证明级数 a (1+a1)(1+a2)-(1+a, 是收敛的 7.证明:若级数∑a与∑b收敛,则级数abn和(an+bn)2也收敛,且 (∑abn)2≤∑a∑b2, ((an+bn)2)2≤(∑a2)2+(Σb2)z