《物理化学》课程教学课件（PPT讲稿）第三章 化学势

一、定义多组分（k个组分）系统中任一容量性质XX=f(T,p, ni, n2, ng,... nk)axaxax+(x)dT +dx =dn, +dnzapaTanp,nkT,nkT,P,n2,ng...nT,p,ni,ng...nkaxdnk..+Onk/T,p,ni,n3...nk-laxaxax2dT+dp+dnaTBaponBB=1p,nkTnJT,P,nc+Bdefax偏摩尔量XB=onBT,p,nc+B13

13 一、定义 多组分（k个组分）系统中任一容量性质X 2 3 1 3 1 3 1 1 2 , , 1 2 , , , , , , , , , k k k k k p n T n T p n n n T p n n n k k T p n n n X X X X dX dT dp dn dn T p n n X dn n −             = + + +                        + +     , , C B def B B T p n X X n     =      X = f(T, p, n1 , n2 , n3 , nk ) , 1 k , , , k C B k B p n T n B B T p n X X X dT dp dn T p n  =          = + +                 -偏摩尔量

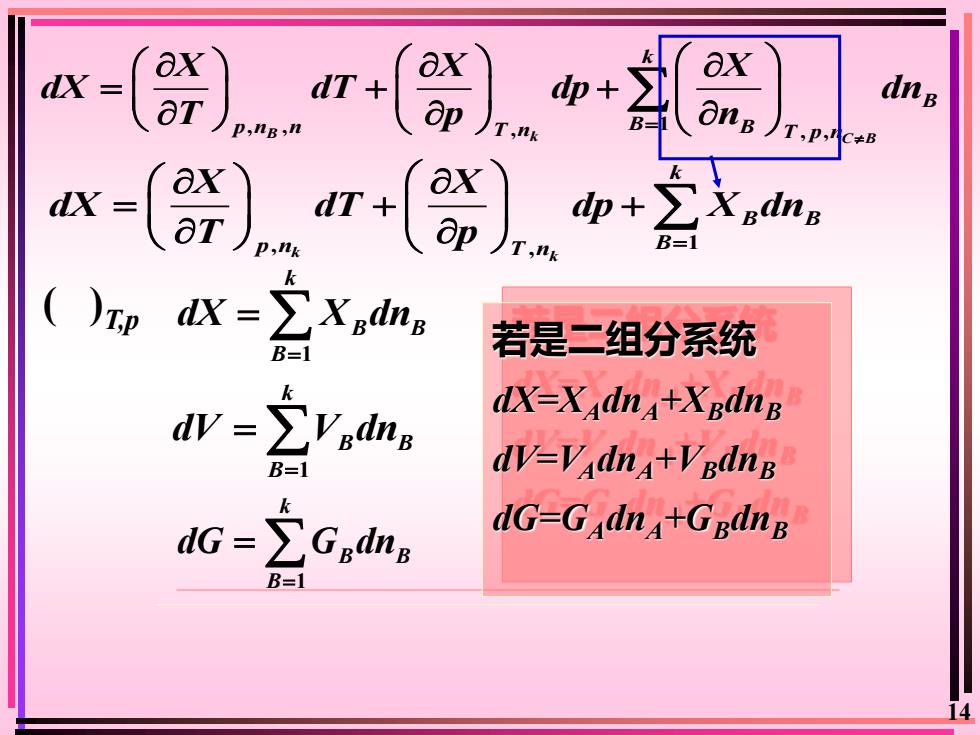
Kaxaxax1dX:dT+dp +dnB一aTOnBapB/T,p,c+BT,nkp,nB,nkaxaxEXednBdxdT +dp +aTopB=1JT,nkp,nkkZXpdnbdX =R若是二组分系统B=1kdX-X.dn+XBdnBdV=ZiVBdngdV-VAdnA+VBdnBB=1kdG-GAdnA+GBdnBEGadndG =B=114

14 , , 1 B , k , , C B k B p n n T n B B T p n X X X dX dT dp dn T p n  =          = + +                 1 k B B B dX X dn = =  1 k B B B dG G dn = =  ( )T,p , 1 k , k k B B p n T n B X X dX dT dp X dn T p =      = + +            1 k B B B dV V dn = =  若是二组分系统 dX=XAdnA+XBdnB dV=VAdnA+VBdnB dG=GAdnA+GBdnB

二、集合公式一系统：A和B的偏摩尔体积分别为VA,VB 则()T,pdV=V.dna+VBdnB如果由纯物质A(n^)，B(nβ)配置该系统：连续加入A和B，并保持系统组成不变，即dna：dnB=na：nB则f"dV = f"^ VAdnA + I"VgdngV= Vana+ VBnB集合公式X= XAnA+XnB16

16 二、集合公式 则 B n A B n A V dV V dn V dn A B    = + 0 0 0 一系统：A和B的偏摩尔体积分别为 VA ,VB 则 ( )T,p dV=VAdnA+VBdnB 如果由纯物质A(nA), B(nB)配置该系统: 连续加入A 和B，并保持系统组成不变，即dnA : dnB = nA : nB V = VAnA+ VBnB X = XAnA+ XBnB -集合公式

axtetX,(om)2B)T,p,n注意：1只有容量性质有偏摩尔量；2.偏摩尔量除了与Tp有关外，还与浓度有关3偏摩尔量本身是强度性质；4 . 单组分系统Xβ=Xm(如: VB=Vm,Gβ=Gm)18

18 注意： 1．只有容量性质有偏摩尔量； 2．偏摩尔量除了与T, p有关外，还与浓度有关； 3．偏摩尔量本身是强度性质； 4．单组分系统XB =Xm (如: VB =Vm , GB =Gm ) , , C def B B T p n X X n    =     

$3.2化学势Chemical PotentialaG一、化学势μB=GBOng )T,p,nc+B二、 化学势的应用19

19 §3.2 化学势 Chemical Potential 一、化学势 二、化学势的应用 , , C B B B B T p n G G n      = =    