
【例附3.2】 已知f=50Hz试求T和o。 【解】 T=1/f=1/50=0.02s o=2πf=2×3.14×50=314rad/s
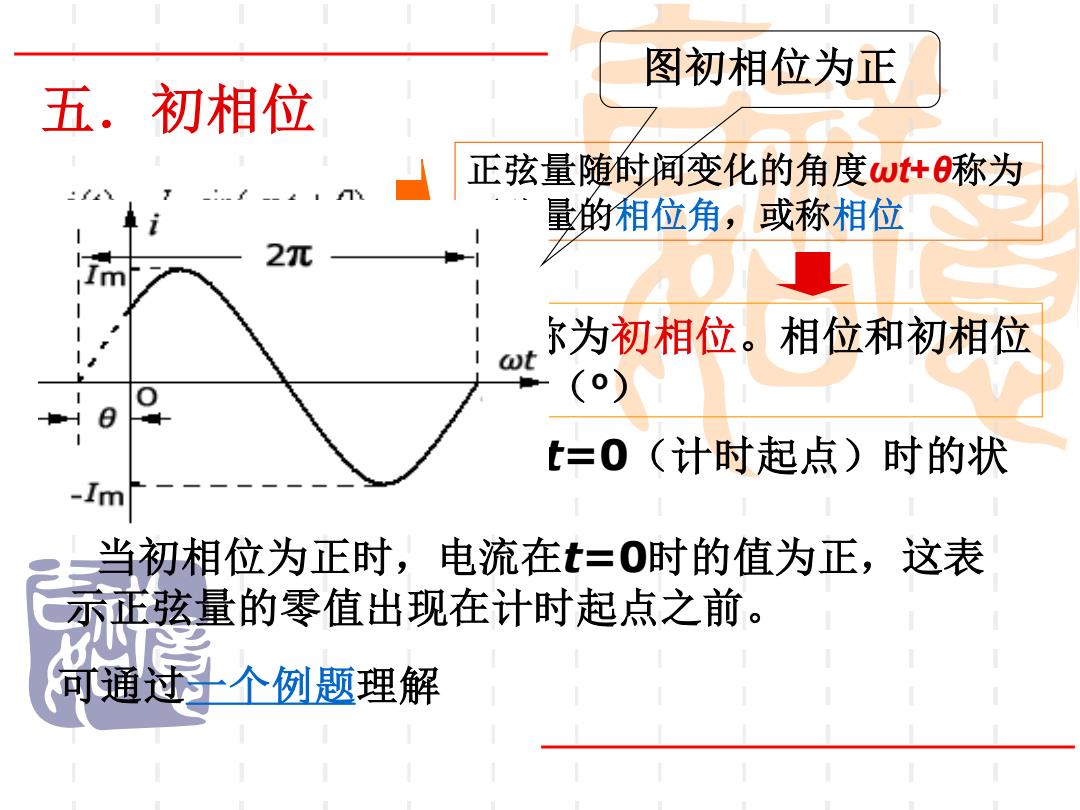
图初相位为正 五.初相位 正弦量随时间变化的角度ωt+称为 量的相位角,或称相位 2元 尔为初相位。相位和初相位 t (0) t=0(计时起点)时的状 Im 当初相位为正时,电流在t=0时的值为正,这表 示正弦量的零值出现在计时起点之前。 可通过个例题理解
五.初相位 θ为t=0时正弦量的相位,称为初相位。相位和初相位 的单位为弧度(rad)或度(o) 正弦量随时间变化的角度ωt+θ称为 正弦量的相位角,或称相位 初相位θ反映了正弦量在t=0(计时起点)时的状 态。 当初相位为正时,电流在t=0时的值为正,这表 示正弦量的零值出现在计时起点之前。 图初相位为正 可通过一个例题理解
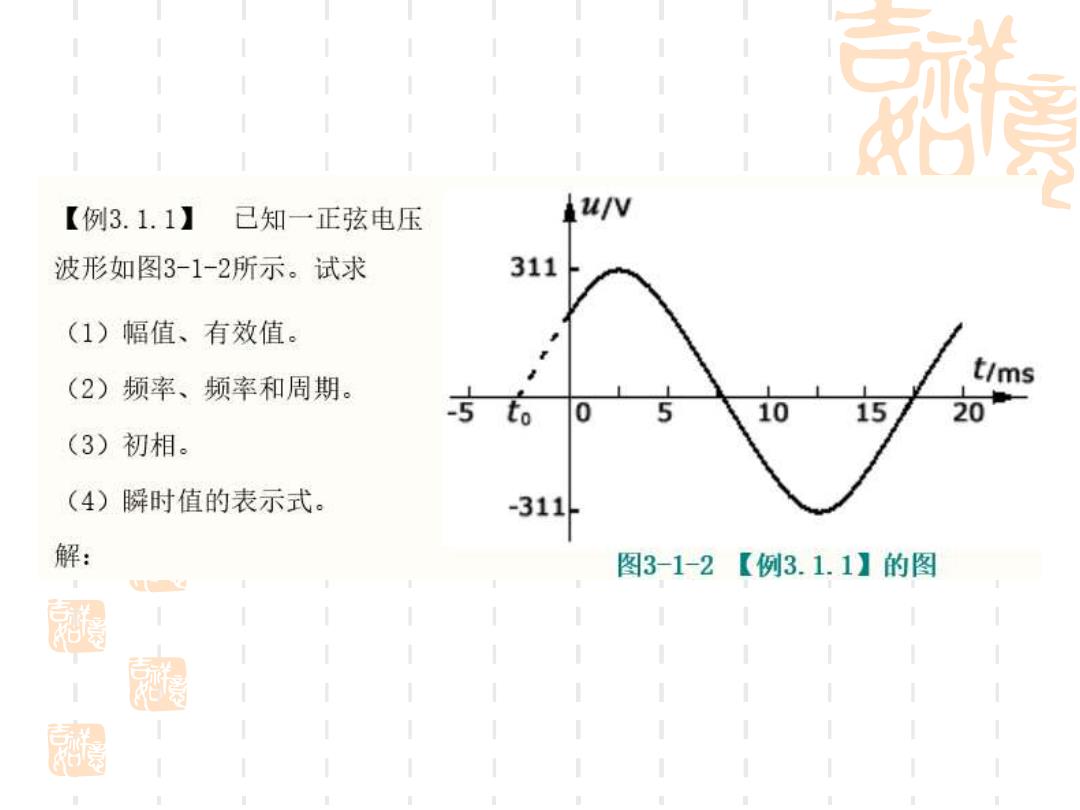
【例3.1.1】 已知一正弦电压 u/V 波形如图3-1-2所示。试求 311 (1)幅值、有效值。 (2)频率、频率和周期。 t/ms 巧右 0 5 10 15 20 (3)初相。 (4)瞬时值的表示式。 -311 解: 图3-1-2 【例3.1.1】的图 履

(1)由图可知幅值 U.=311W 所以,有效值 .=2207 (2)周期T=(17.5+2.5)×103=20ms,所以,频率、角频率为 1 20x10寸=502 2n2n = 20x10寸=100r (3)初相的绝对值引8为 4,=100e×25x103=。 由于正弦波的零值出现在坐标原点(计时起点)之前,所以初相为正,故得初相日 π =rad 4 (4)所以正弦电压波形的瞬时值表示式为 u)=311sin(100πt+zV 4

同频率两个正弦量的 两个正弦量的相 相位差等于它们的初 位差等于它们的相 相位之差,相位差是 位相减 一个与时间无关的常 数(解柽) 可学习两个正弦量的相位同相(解释)、 “超前”、“滞后”、反相等相关术语(解
两个正弦量的相 位差等于它们的相 位相减 同频率两个正弦量的 相位差等于它们的初 相位之差,相位差是 一个与时间无关的常 数(解释) 可学习两个正弦量的相位同相(解释)、 “超前” 、 “滞后”、反相等相关术语(解 释)