
在正弦交流电路中,经常遇到的是频率相同的正弦量。例如,设两个同频率的正弦量以、 i,分别为 u=U sin(at+e) i=I sin(@t+e) 它们的初相位分别为民、:; 同频率的两个正弦量的相位差等于它们的相位相减。如设中表示电压和电流之间的相位差,则 有 =(ωt+民)-(wt什日)=民,-日 (3-1-5) 上述结果表明,同频率两个正弦量的相位差等于它们的初相位之差,相位差是一个与时间无 关的常数
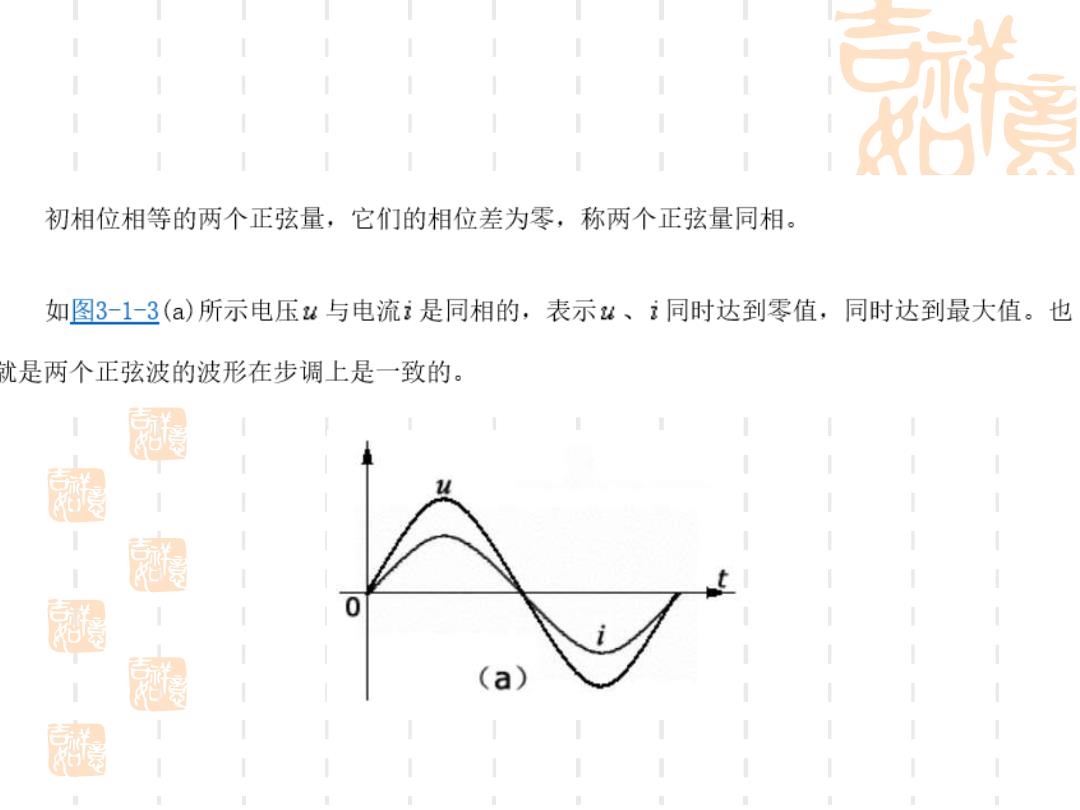
初相位相等的两个正弦量,它们的相位差为零,称两个正弦量同相。 如图3-1-3()所示电压u与电流i是同相的,表示u、i同时达到零值,同时达到最大值。也 就是两个正弦波的波形在步调上是一致的。 涵 0 (a)

设两个同频率的正弦量u、i,分别为 u=sin(at+8.) i=sin(四t+8) 素 它们的初相位分别为民、只; 同频率的两个正弦量的相位差等于它们的相位相减。如设中表示电压和电流之间的相位 差,则有 p=(ωt+民)-(ωt+8)=民-日 当中>0时,称为u超前i一个角度中;当中<0时,称为u滞后i一个角度中;当中=二时,称 为“与正交(如图3-13());当x时,称为u与i反相(如图313。)。2 相位差也是主值范围内取值,即相位差的绝对值|φ|≤π。 (b

六.正弦量的相量表示 一个正弦量是由它的幅 在线性交流电路中,电路的全部 值、角频率和初相位三 稳态响应都是同频率的正弦量, 个要素所决定的 只有幅值与初相位是未知的。 可用一个复数同时表示一个正弦量的幅值和初相位,这个代表 正弦量的复数,取一个特殊的名字,称为相量(解释见书 P55) i=In sin(at+e) in =.=In!e 正弦电流的相应相量如上(用大写字母,上加小圆点表示) 显然,)上面的相量为电流幅值相量,当然也存在有效值相量,电 压相量等
六.正弦量的相量表示 一个正弦量是由它的幅 值、角频率和初相位三 个要素所决定的 在线性交流电路中,电路的全部 稳态响应都是同频率的正弦量, 只有幅值与初相位是未知的。 可用一个复数同时表示一个正弦量的幅值和初相位,这个代表 正弦量的复数,取一个特殊的名字,称为相量(解释见书 P55) 正弦电流的相应相量如上(用大写字母Im,上加小圆点表示) 显然,上面的相量为电流幅值相量,当然也存在有效值相量,电 压相量等

i=In sin(at+8) →im=lne=1n/e Im 相量在复平面上的图形称为相量图,正弦电流的幅值、有效 值相量如上 既然相量是复数,当然可以进行运算 正弦量的和的相量等于各正弦量的相量相加 (复数相加) 正弦量的差的相量等于各正弦量的相量相减 (复数相减) 可参照复数的乘除运算理解相量的乘除
可见相量是一个复数(复 习复数方面的数学知识 ), 它与上述给定频率的正弦量 有一一对应关系 相量与正弦量之间存在着一 一对应的关系。但不能说相 量等于正弦量,这因为相量 没有反映正弦量的角频率 相量在复平面上的图形称为相量图,正弦电流 的幅值、有效 值相量如上 既然相量是复数,当然可以进行运算 正弦量的和的相量等于各正弦量的相量相加(复数相加) 正弦量的差的相量等于各正弦量的相量相减(复数相减) 可参照复数的乘除运算理解相量的乘除