
§1 单纯形法的基本思路和原理 当所有的x1≥0,且0≤0,此时 》ys0 实际上目标函数: 2=+∑,x,=+(∑ O,x)+( X) ie. x,为基向量 x,为非基向量 基变量均≥0,检验数都为0,0,x,=0;非基变量的检验 数均≤0,只有非基变量都为0,才有0x0。此时目标
§ 1 单纯形法的基本思路和原理 当所有的 x j ≥0,且σj ≤0,此时 实际上目标函数: 基变量均≥0,检验数都为0,σ s x s =0;非基变量的检验 数均≤0,只有非基变量都为0,才有σ t x t =0 。此时目标 函数才能取最大值z0。 0 0 s t x j j s s t j J x t z z x z x x 为基向量 为非基向量 ( )( ) 0 j j j J x

§1 单纯形法的基本思路和原理 三、基变换 例题中1,02>0,即该基本可行解不是最优解,需 进行基变换。 具体做法:更换可行基中的一个列向量,得到新的 可行基,求出新的基本可行解使目标函数值更优。 为了换基要确定换入变量-入基变量与换出变量- 出基变量
§ 1 单纯形法的基本思路和原理 三、基变换 例题中 σ1,σ2>0,即该基本可行解不是最优解,需 进行基变换。 具体做法:更换可行基中的一个列向量,得到新的 可行基,求出新的基本可行解使目标函数值更优。 为了换基要确定换入变量---入基变量与换出变量--- 出基变量
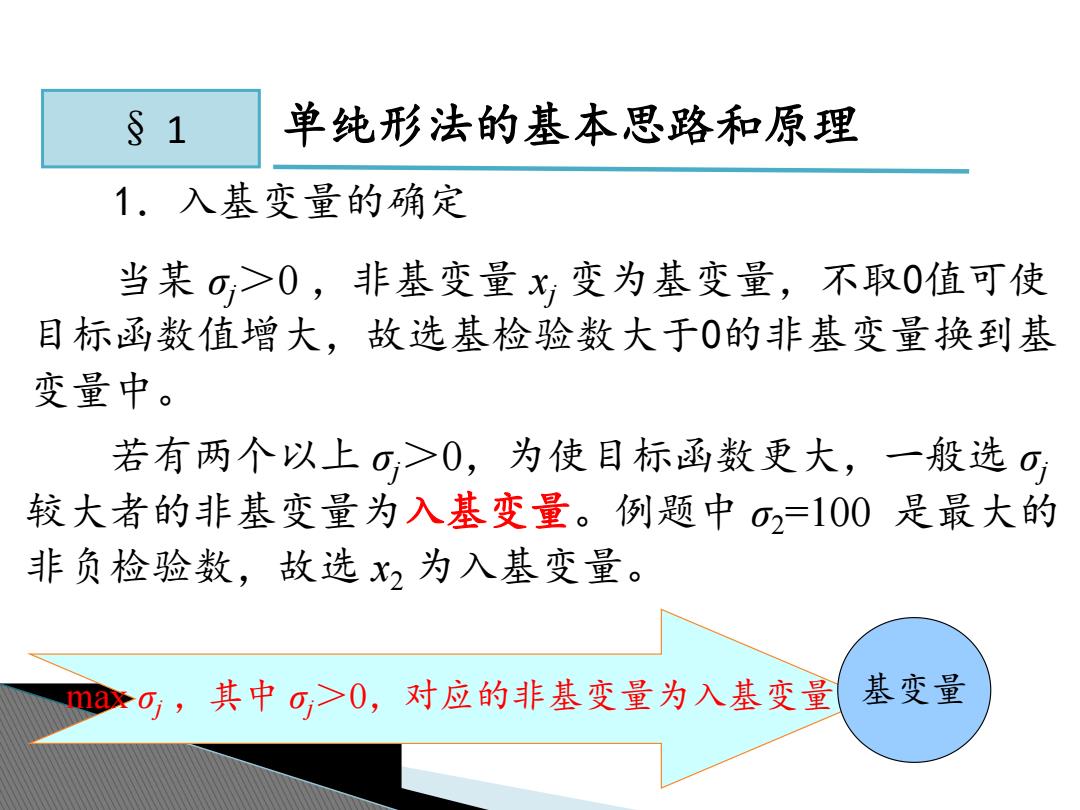
§1 单纯形法的基本思路和原理 1.入基变量的确定 当某o>0,非基变量x变为基变量,不取0值可使 目标函数值增大,故选基检验数大于0的非基变量换到基 变量中。 若有两个以上o>0,为使目标函数更大,一般选0 较大者的非基变量为入基变量。例题中02=100是最大的 非负检验数,故选x2为入基变量。 n0,其中o>0,对应的非基变量为入基变量 基变量
§ 1 单纯形法的基本思路和原理 1.入基变量的确定 当某 σj>0 ,非基变量 xj 变为基变量,不取0值可使 目标函数值增大,故选基检验数大于0的非基变量换到基 变量中。 max σj ,其中 σj>0,对应的非基变量为入基变量 基变量 若有两个以上 σj>0,为使目标函数更大, 一般选 σj 较大者的非基变量为入基变量。例题中 σ2=100 是最大的 非负检验数,故选 x2 为入基变量

§1 单纯形法的基本思路和原理 2.出基变量的确定 确定入基变量后,需在原来的基变量S1,S2,S3中 选一个出基变量。若心?作为出基变量,则新的基变量为 x2,S1,S2,非基变量x1=S30,方程组变为: x2+51=300, x2+S2=400, x2=250. 得基本解:x=0,x=250,51=50,S2=150,53=0。此解 基本可行解
§ 1 单纯形法的基本思路和原理 2.出基变量的确定 确定入基变量后,需在原来的基变量 s1,s2,s3 中 选一个出基变量。若 s3 作为出基变量,则新的基变量为 x2,s1,s2,非基变量 x1=s3=0,方程组变为: x2 + s1 = 300, x2 + s2 = 400, x2 = 250. 得基本解:x1=0,x2=250,s1=50,s2=150,s3=0。此解 满足非负条件,是基本可行解
§1 单纯形法的基本思路和原理 如何在求解以前来确定 出基变量,使得求出的 解是可行解?
§ 1 单纯形法的基本思路和原理 如何在求解以前来确定 出基变量,使得求出的 解是可行解?