
管理浮动机制下的人民币汇率行为分析 ·115· 管理浮动机制下的人民币汇率行为分析 一基于贝叶斯MCMC推断法与ESVDJ模型” 童汉飞1陈浪南2 (1.厦门大学经济学院;2.中山大学岭南学院) 【摘要】本文提出一种汇率行为的理论模型一ESVDJ模型,并对该模型的估 计设计出贝叶斯MCMC推断法。实证研究表明,在管理浮动汇率机制下,人民币 汇率的日常波动持续地维持在较小范围。但如果市场供求双方发生显著的失衡,人 民币汇率将产生跳跃行为,由此引发异常的汇率风险。此外,外汇市场并不显著地 存在类似于权益市场的杠杆效应。本文同时对ESVD]模型与通常的随机波动性模 型SV及SV叮模型进行对比。MCMC似然比检验与密度函数非参数估计表明,后 两者存在较大的设定错误。本文最后对汇率风险监管提出政策建议。 关键词人民币汇率跳跃MCMC推断ESVDJ 中图分类号F830文献标识码A An Analysis of RMB Exchange Rate Behavior Based on MCMC Method and ESVDJ Model Abstract:In this paper,we propose a new theoretical model,ESVDJ,to de- scribe the dynamic behavior of exchange rate between RMB and foreign currencies, as well as to design a MCMC inference algorithm for estimating the model.The em- pirical results employed in this model suggest that the daily change of RMB is con- strained in small scope with highly persistent volatility.However,RMB may pro- duce jumps when foreign exchange market encounters serious imbalance between demand and supply.Furthermore,RMB exchange market does not have significant leverage effect after taking account on the existence of jumps.Finally,the paper provides a MCMC ratio and nonparametric test for the SV,SVJ and ESVDJ,and test result favors our ESVDJ model. Key words:MCMC;Jump;RMB Rate;ESVDJ 前。言 人民币汇率形成机制在过去的两年中发生了显著的变化。首先是央行于2005年7月21 ①感谢中山大学龄南学院王美今教授,以及美国康奈尔大学洪永森教授的建议,当然文资自负, 万方数据
管理浮动机制下的人民币汇率行为分析 ·115· 管理浮动机制下的人民币汇率行为分析 ——基于贝叶斯MCMC推断法与ESVDJ模型① 童汉飞1 (1.厦门大学经济学院; 陈浪南2 2.中山大学岭南学院) 【摘要】本文提出一种汇率行为的理论模型——ESVDJ模型,并对该模型的估 计设计出贝叶斯MCMC推断法。实证研究表明,在管理浮动汇率机制下,人民币 汇率的日常波动持续地维持在较小范围。但如果市场供求双方发生显著的失衡,人 民币汇率将产生跳跃行为,由此引发异常的汇率风险。此外,外汇市场并不显著地 存在类似于权益市场的杠杆效应。本文同时对ESVDJ模型与通常的随机波动性模 型sv及SⅥ模型进行对比。MCMC似然比检验与密度函数非参数估计表明,后 两者存在较大的设定错误。本文最后对汇率风险监管提出政策建议。 关键词人民币汇率跳跃MCMC推断ESⅥDJ 中图分类号F830 文献标识码A An Analysis of RMB Exchange Rate BehaVior Based : on MCMC Method and ESVDJ Model Abstract: In this paper, we propose a new theoretical model, ESV]DJ, to de— scribe the dynamic behavior of exchange rate between RMB and foreign currencies, as well as to design a MCMC inference algorithm for estimating the model.The em— pirical results employed in this model suggest that the daily change of RMB is con— strained in sman scope with highly persistent v01atility.However,RMB may pro— duce jumps when foreign exchange market encounters serious imbalance between demand and supply.Furthemore, RMB exchange market does not have significant leverage effect after taking account on the e五stence of j umpS.Finally, the paper provides a MCMC ratio and nonparametric test for the SV, SⅥand ESVDJ, and test result favors our ESvDJ model. Key words:MCMC;Jump;RMB Rate;ESln)J 前 言 人民币汇率形成机制在过去的两年中发生了显著的变化。首先是央行于2005年7月21 ①感谢中山大学岭南学院王美今教授,以及美国康奈尔大学洪永淼教授的建议,当然文责自负。 万方数据

·116 《数量经济技术经济研究》2007年第11期 日颁布实行以市场供求为基础的、参考一篮子货币进行调节的管理浮动汇率制度。后又于 2005年年底引人做市商交易方式,以试图进一步促进市场的流动性与交易效率。由此产生 一个值得探讨的问题,即在外汇市场微观结构发生改变的情况下,人民币汇率具有怎样的行 为特征?对该问题的分析,不仅对商业银行、非银行金融机构和金融监管机构的外汇风险管 理具有借鉴意义,同时也是进一步深入研究人民币远期汇率、期权定价及其市场管理的基础。 然而,我国理论界关于人民币汇率问题的研究现状是:第一,众多学者几乎将全部的关 注点集中于人民币均衡汇率,或人民币汇率贬值、升值幅度对各产业发展影响的分析上,该 方面的论文也极其浩瀚。例如,张晓朴(1999)、Zhang(2001)、林伯强(2002)和张斌 (2003)等人分析了自东亚货币危机以来,人民币均衡实质汇率问题。魏巍贤(2006)讨论 了人民币升值的宏观经济影响。直接深入研究汇率动态行为的文献几乎很少,甚至可谓非常 罕见,但汇率的动态行为分析,对微观经济个体而言,具有直接的现实意义。并且该问题的 研究,是解决汇率风险防范对冲、外汇资产套期保值与人民币衍生品定价等诸多问题的前提 条件。例如,“中航油事件”的爆发及其最终所致的破产案例,一方面暴露了我国金融风险 监督管理制度的缺陷,同时也表明我们快乏对金融产品变化行为的深刻把握,无法及时预警 交易中出现的重大风险。第二,尽管存在相关的文献,直接研究汇率自身的动态行为与相应 的汇率风险控制等问题,如林伟斌与陈浪南(2007),但大多采用一般的时间序列模型,如 B一S模型或协整回归模型,研究方法过于单一陈旧。另一个重要的不足之处是,没有反映 国际金融研究的最新进展与发现。 Carr (2007),Eberlein Madan (2007),Song (2006),Duan (2005),Eraker (2004)以及Duie等(2002)的研究发现,金融市场可以在短时间内发生大规模的价格变 化,由此呈现出一种向上或向下的跳跃行为(jump),并引发跳跃性风险((jump risk)。金 融市场的跳跃性行为,尤其是大幅的下跌,意味着巨额资金在投资者之间的转移,这将直接 导致部分投资者破产(如中航油、巴林银行),进而引起金融体系的崩溃和社会的不稳定。 金融市场的跳跃现象,在历史上是如此频繁地涌现。例如,在1987年10月19日的黑 色星期一中,美国股市下跌了23%,使得美国资本市场损失了1万亿美元;从1990年开始 日本股市出现大幅下跌现象,日经指数从1989年末的39000点跌至3年后的17000点,整 个日本的资本市场损失了2.7万亿美元;在1994年的债券灾难中,美国联邦储备银行连续 六次提高利率,全球资本市场损失了约1.5万亿美元;美国奥兰治郡(Orange county)的 一揽子投资,包括郡、市、学校等属于地方政府的75亿美元的组合投资,在1994年12月 一个月中损失了16.4亿美元,这是历史上最大的地方政府破产案;在1997~1998年亚洲金 融危机期间,亚洲货币在短期内大幅贬值(Wo0等,2000),等等。 那么是何种原因引发金融市场的跳跃行为与跳跃风险呢?对此国际理论界存在多种解 释,例如市场发展的不完善性、政策的调整(policy adjustment).、重大不利消息的公布、 投机力量的攻击以及其他金融市场的风险溢出效应(risk spillover)与国际间传染性(con- tagion)皆有可能导致市场突然间大幅度下滑。 由于市场的该种行为对金融风险防范、投资组合管理、衍生品定价与金融体系稳定性等 众多领域产生了深远的影响,因此国际理论界近期对此问题的相关领域展开了密集的研究。 例如Li(2006),Ma(2007),Hong等(2006). 本文在研究汇率的动态行为时,一个重要的目标是将跳跃行为考虑到汇率的变化过程 中。国家外汇管理局于2006年度明确表示,将逐步放宽汇率的波动幅度管理,以促进汇率 万方数据
·116· 《数量经济技术经济研究》2007年第11期 日颁布实行以市场供求为基础的、参考一篮子货币进行调节的管理浮动汇率制度。后又于 2005年年底引入做市商交易方式,以试图进一步促进市场的流动性与交易效率。由此产生 一个值得探讨的问题,即在外汇市场微观结构发生改变的情况下,人民币汇率具有怎样的行 为特征?对该问题的分析,不仅对商业银行、非银行金融机构和金融监管机构的外汇风险管 理具有借鉴意义,同时也是进一步深入研究人民币远期汇率、期权定价及其市场管理的基础。 然而,我国理论界关于人民币汇率问题的研究现状是:第一,众多学者几乎将全部的关 注点集中于人民币均衡汇率,或人民币汇率贬值、升值幅度对各产业发展影响的分析上,该 方面的论文也极其浩瀚。例如,张晓朴(1999)、Zhang(2001)、林伯强(2002)和张斌 (2003)等人分析了自东亚货币危机以来,人民币均衡实质汇率问题。魏巍贤(2006)讨论 了人民币升值的宏观经济影响。直接深入研究汇率动态行为的文献几乎很少,甚至可谓非常 罕见,但汇率的动态行为分析,对微观经济个体而言,具有直接的现实意义。并且该问题的 研究,是解决汇率风险防范对冲、外汇资产套期保值与人民币衍生品定价等诸多问题的前提 条件。例如,“中航油事件”的爆发及其最终所致的破产案例,一方面暴露了我国金融风险 监督管理制度的缺陷,同时也表明我们缺乏对金融产品变化行为的深刻把握,无法及时预警 交易中出现的重大风险。第二,尽管存在相关的文献,直接研究汇率自身的动态行为与相应 的汇率风险控制等问题,如林伟斌与陈浪南(2007),但大多采用一般的时间序列模型,如 B—S模型或协整回归模型,研究方法过于单一陈旧。另一个重要的不足之处是,没有反映 国际金融研究的最新进展与发现。 据Carr(2007),Eberlein与Madan(2007),Song(2006),DIuan(2005),Eraker (2004)以及Duffie等(2002)的研究发现,金融市场可以在短时间内发生大规模的价格变 化,由此呈现出一种向上或向下的跳跃行为(jump),并引发跳跃性风险(jump risk)。金 融市场的跳跃性行为,尤其是大幅的下跌,意味着巨额资金在投资者之间的转移,这将直接 导致部分投资者破产(如中航油、巴林银行),进而引起金融体系的崩溃和社会的不稳定。 金融市场的跳跃现象,在历史上是如此频繁地涌现。例如,在1987年10月19日的黑 色星期一中,美国股市下跌了23%,使得美国资本市场损失了1万亿美元;从1990年开始 日本股市出现大幅下跌现象,日经指数从1989年末的39000点跌至3年后的17000点,整 个日本的资本市场损失了2.7万亿美元;在1994年的债券灾难中,美国联邦储备银行连续 六次提高利率,全球资本市场损失了约1.5万亿美元;美国奥兰治郡(Orange county)的 一揽子投资,包括郡、市、学校等属于地方政府的75亿美元的组合投资,在1994年12月 一个月中损失了16.4亿美元,这是历史上最大的地方政府破产案;在1997~1998年亚洲金 融危机期间,亚洲货币在短期内大幅贬值(woo等,2000),等等。 那么是何种原因引发金融市场的跳跃行为与跳跃风险呢?对此国际理论界存在多种解 释,例如市场发展的不完善性、政策的调整(policy adjustment)、重大不利消息的公布、 投机力量的攻击以及其他金融市场的风险溢出效应(risk spillover)与国际间传染性(con— tagion)皆有可能导致市场突然间大幅度下滑。 由于市场的该种行为对金融风险防范、投资组合管理、衍生品定价与金融体系稳定性等 众多领域产生了深远的影响,因此国际理论界近期对此问题的相关领域展开了密集的研究。 例如Li(2006),Ma(2007),Hong等(2006)。 本文在研究汇率的动态行为时,一个重要的目标是将跳跃行为考虑到汇率的变化过程 中。国家外汇管理局于2006年度明确表示,将逐步放宽汇率的波动幅度管理,以促进汇率 万方数据

管理浮动机制下的人民币汇率行为分析 ·117· 形成的自由度与弹性。在这种背景下,我们可以预期外汇市场也可能产生其他金融市场所呈 现出的跳跃现象,并引发异常的汇率风险。这种异常行为的分析,对于进一步的人民币远期 汇率、期权合理定价是非常必要的。 本文另一个目标是引人贝叶斯MCMC推断法。MCMC基本原理是在Gibbs与Metrop- olis抽样算法的基础上,获得马尔科夫链(Markov chains),以此逼近分布函数复杂甚至未 知的参数与状态变量。MCMC的优点是可以同时推断出参数与状态变量,并能够有效地避 免理论模型极度复杂的情况下,一般最优算法的无效性难题。例如,极大似然估计法 (MLE)与广义矩方法(GMM)。因此,在近几年中,该方法受到国际学术界的广泛关注, 并成功地被应用于宏观经济学、金融工程以及信息科学等众多领域中。但国内尚没有文献较 为深人介绍经济模型的MCMC设计。本文针对笔者所提出的汇率理论模型,给出具体MC MC推断法的构造,以阐述其基本原理及其应用价值。 一、汇率的理论模型 一般地,在对汇率动态过程建立模型时,可以采用基于扩散(diffusion)的随机波动性 模型,如B-S或SV模型,或ARCH类模型。在早期巴塞尔资本协议所倡导的Credit Metrics风险管理体系中(J.P.Morgan,1997),基本上也是应用该类理论模型对银行信贷 与外汇资产的风险进行监控。但Eraker(2004),Eraker,Johannes与Polson(2003), Carr(2007)等人的研究表明该类模型存在显著的缺陷,因为扩散过程(diffusion process) 很难产生巨幅的变化,由此无法合理地解释金融资产价格为什么会在短暂的时间内,发生如 此大规模的运动,并最终呈现出一种向下或向上的跳跃(jump)现象。由此,Eraker (2004)以及Duffie等(2002)提出SVDJ模型对金融价格进行建模。本文在Eraker等人的 基础上,提出以下的汇率模型①: N,(P) =(,+V)d+Wawm(P)+(2s。-(m-1D) S, (1) j-l N,(P) diogv,=k (0-logV-)dt+a,W:(P)+d(Z (P)) (2) =1 其中,S表示即期汇率过程,V.代表汇率的随机波动性变量。W:(P)和W:(P)是 在概率测度P下相关的标准布朗运动,相关系数为P,即E(W:W?)=ρ。该相关系数用于 反映人民币汇率波动可能涵括的杠杆效应(leverage effect)。N,(P)是泊松计数过程,类 似于McCurdy(2004),Eraker(2004),Duan(2005),Duffie(2002),我们以此表示汇率 过程中可能存在的跳跃行为,其中λ,与;分别表示跳跃强度为与跳跃时间。乃表示波动性 风险溢价,通过引入该系数,我们可以分析在汇率发生跳跃行为的情况下,是否存在显著的 波动性风险溢价。进一步地,我们假定波动性与汇率的收益过程有着相同时期的跳跃来临时 刻。给定波动性的跳跃幅度满足Z(P)~exp(,),收益的跳跃幅度则满足Z☑(P)|Z~ N(4,十p,Z,d)。,表示汇率的漂流率,参数0是波动性的长期均值,E(V,)=0,而。 则度量了汇率波动性向长期均值回归的速率。S。-满足: ①本文将之称为ESVD模式(Exponential stochastic volatility with double jump factors), 万方数据
管理浮动机制下的人民币汇率行为分析 ·117· 形成的自由度与弹性。在这种背景下,我们可以预期外汇市场也可能产生其他金融市场所量 现出的跳跃现象,并引发异常的汇率风险。这种异常行为的分析,对于进一步的人民币远期 汇率、糍权合理定价是毒≥豢必要的。 本文另一个目标是引入贝叶斯MCMC推断法。MCMC基本原理怒在Gibbs与Metrop— 01is抽样算法的基础上,获得马尔科夫链(Markov chains),以此逼近分布函数复杂甚至朱 翔的参数与状态变量。氧憾MC的优点是可以同时推赞出参数与状态变量,并熊够有效邈避 免理论模型极度复杂的情况下,一般最优算法的无效性难题。例如,极大似然估计法 (MLE)与广义矩方法(GMM)。因此,在近几年中,该方法受到国际学术界的广泛关注, 莠成功建被应用予宏溪经济学、金磁工程泼及信患科学等众多领域中。僵国内尚没有文献较 为深入介绍经济模型的MCMC设计。本文针对笔者所提出的汇率理论模型,给出具体MC— MC推断法的构造,以阐述其基本原理及其应用价值。 一、汇率的理论模型 一般邋,在对汇率动态过程建立模型时,可以采蔫基予扩散(di嚣联sion)嚣随槐波动憔 模型,如B—S或sv模型,或ARCH类模型。在早期巴塞尔资本协议所倡导的Credit Metrics风险管理体系中(J,P.Morgan,1997),基本上也是应用该类理论模型对银行信贷 与外汇资产的风险进行监控。徨Erakef(2∞矮),Efal【er,Joh雒摭es与&lso拄(z003), Carr(2007)等人的研究表明该类模型存在显著的缺陷,因为扩散过程(diffusion process) 很难产生巨幅的变化,由此宪法合理地解释金融资产价格为什么会在短暂的时间内,发生如 此大规模的运动,并最终娶现出一释向下或商主懿跳跃(jump)现象。患诧,Eraker (2004)以及Duffie等(2002)提出SⅧJ模型对金融价格进行建模。本文在Eraker等人的 基础上,提出以下的汇率模型①: 孥一(吩+以)卅国w(p)+(警蹦和Ⅷ) 捷(砖 矗logE=毛(免一lo套K一)出+如w警(哟+d(∑露(p)) (2) 其中,S表承即期汇率过程,Ⅵ代表汇率的随机波动性变量。职(P)和职(P)是 在概率测度P下相关的标准布朗运动,耀关系数海p,郎E(弼孵)一lD。该裰关系数蔫于 反映人民币汇率波动可能涵括的杠杆效应(1everage effect)。N(尹)是泊松计数过程,类 似于McCurdy(2004),Eraker(2004),Duan(2005),Duffie(2002),我们以此表示汇率 过程中可能存在的跳跃行为,其中丸与c,分别表示跳跃强凄为与跳跃时间。瞒表示波动性 风险溢价,通过引入该系数,我们可以分析在汇率发生跳跃行为的情况下,是否存在显著的 波动性风险溢债。进一步地,我们假定波动性与涎率的收益过程有着棚同时期的跳跃来临时 刻。给定波动性的跳跃幅度满足露(p)~exp(鳓),收益的跳跃幅度剃满足露(砂|露~ N(雎十BZ;,Z)。n表示汇率的漂流率,参数口是波动性的长期均值,E(K)=口,而愚。 剃度量了汇率波动性向长期均值回归的速率。&一满跫: ① 本文将之称为艇ⅣDJ模式(Exponential stochstic、,olatility丽th double jump factors)。 万方数据

·118… 《数量经济技术经济研究》2007年第11期 S-=limS (3) 上+可 相对于权益市场,外汇市场的波动性幅度通常较小,为了防止随机抽样中可能产生的负波 动性现象。因此不同于Eraker(2004),Duffie(2002)以及i等(2006)的研究,我们采用对 数函数对波动性建模。本文提出的ESVD模型可以涵括多数流行的波动性模型,例如固定波 动性BS模型,指数随机波动性SV模型(Henston,l992),以及Bates的灯模型(1996)。 对ESVD]模型进行欧拉时间离散化,我们最终可以将(1)式与(2)式表示为以下的 离散方程式: Ym1a-Ya=(u+%Va)△+√Wa△ei41a+J+DaZi+ (4) logV+ia=(an十B.logV)△+ae+a十Je+aZ+iDa (5) 其中,Ya是复合收益率,即Y=log(Sa);△是时间的离散间隔区间(本文选择日间 隔);e+)a与e+Da是标准维纳过程;J+Da是贝努利随机变量(Bernoulli). 二、模型的MCMC推断估计法 本部分给出ESVDJ模型的MCMC推断方法。MCMC推断法的基本原理源于Clifford一 Hammersley理论,是一种通过贝叶斯后验分布,抽样出马尔科夫链以逼近模型的状态变量 与参数。对本文的ESVDJ模型,其参数与状态空间分别为: ⑧={μ,h,ao,A,h,,,p,a,,State_V={J,Z,Z,V) (6) 跟据贝叶斯法则,可以将参数与状态变量(State_S)的后验概率密度表示为: p{8,J,2,2,VIY心p(Y|⊙,J,2,2,p(⊙,J,2,2,(7) 其中,p(Y|⊙,J,2,2,为似然函数,p(⊙,J,2,Z,)先验分布。在通 常情况下,我们很难获得似然函数的表达式(如本文的ESD模型),或因其过于复杂难以直 接抽样。对此难题,MCMC推断法运用Clifford-Hammersley定理,将系数与状态变量的后验 分布函数进行分解加以解决。本文的模型估计推断,可以通过以下MCMC迭代方式进行: 参数:p(⑧|⊙-,J,Z,Z,V,Y),i=1,,k 跳跃时间:p(Ja=1|⊙,2,2,V,Y,t=1,…,T 跳跃幅度:p(Z|©,,Ja=1,V“,Y),t=1,“,T (8) p(28|⊙,Ja=1,Va,Z,Y)t=1,…,T 波动性:p(Va|V+a,V(ea,8,J+J(-DA,Y,2,Z),t=1,…,T 假定该种方式所获取的马尔科夫链为{⑧,J”,Z,Z®,V9①,我们由此 可以采用∑,f(6)/C等方式来推断模型的参数与状态变量。在设计MCMC推断法时, 应恰当定义参数的先验分布类型,然后采用Gibbs或Metropolis一Hasting算法抽样后验 样本。 ①Johnnnes与Polson(20o3)表明,核种方式抽样形成的样本,将淅进地通近参数或状况变量的平稳随机分布, 万方数据
·118· 《数量经济技术缎济研究》2∞7年第ll期 &一2li翻瓯 (3) p口 相对于权益市场,外汇市场的波动性幅度通常较小,为了防止随机抽样中可能产生的负波 动性现象。因此不同予Eraker(2004),n般e(2002)以及“等(2006)的研究,我们采用对 数函数簿波动性建模。本文提赉的至&刀礴模型可敬澄括多数流行的波动性模型,例如固定波 动性BS模型,指数随机波动性睽Ⅳ模型(HenstI。n,1992),以及Bat鹤的SⅥ模型(1996)。 对联ⅣDJ模型进行欧拉时间离散化,我们最终可以将(1)式与(2)式表示为以下的 离散方程式: y(州)A—k一(p+啦%)△+~/蕊{件1)A十J(件1)△苏外1) log妖一1)厶=(渤÷磊lo裔‰)△+鼬己+1疆÷J“+1)矗忍十1)矗 (4) (S) 其中,k是复合收益率,即k=109(S地);△是时间的离散间隔区间(本文选择日间 隔)}£辑l》矗与£艺+l冶是标准维纳过程;歹《辩1)△是员努麓l随枧变爨(Berno娃lli)。 二、模型的MCMC推断估计法 本部分给出ESv】DJ模型的MCMC推断方法。MCMC推断法的基本原理源于C1ifford— Hammersley理论,是一种通过贝叶斯后验分布,抽样出马尔科夫链以逼近模型的状态变量 与参数。对本文的ESV聪模篓,其参数与状态空阕分别为: @一{户,珈,舶,届,胁,Z,Z,lD,B,A),S£口地一V;{.厂,zJ,矛,V) (6) 跟据贝叶斯法曼|l,可以将参数与状态变量(S蹴踟一S)的蔚验概率密度表示隽: 夕{@,,,乃,矛,V l y)∞户(y l@,J,矛,矛,y)户(@,J,Z,,汐,y)(7) 其中,≯(y l@,歹,Z,矛,聊为似然函数,痧(@,歹,Z,2,D先验分布。在通 常情况下,我们稷难获得截然函数盼表达式(如本文的琰;锄模型),或因其过于复杂难泼直 接抽样。对此难题,M卟忙推断法运用aiffo沾Hammersley定理,将系数与状态变量的后验 分布函数进行分解加以解决。本文的模型馈计推断,可以通过以下M呱配迭代方式进行: 参 数:P(馥|@一i,歹,Z,孑,y,y), i=l,…,志 跳跃时间:p(J融=1 l@,ZJ,刃,y,y), £=1,…,T 跳跃幅度:p(玩l@,汐,歹啦一王,%,D,£=王,…,丁 (8) P(Z翟|@,J地一l,V吐,Zk,Y) t=1,…,T 波动性:p(‰I V(件1)厶,ⅥH)△,@,J(m)△,,∽1)△,y,刃,刀),£=1,…,T 假定该种方式所获取豹马尔辩夫链为{e涵,歹鼬,Z|(掌),z铽鄯,≯;’}嘉,◇,我们由此 可以采用∑三|,,(伊)/G等方式来推断模型的参数岛状态变最。在设计McMc推断法时, 应恰当定义参数的先验分布类型,然后采用Gibbs或Metropolis一}{asti遮算法抽样后验 样本。 ①Joh蝴n妫与Polson(2003)表嬲,该种方式抽样形成的样奉,将渐进地濑近参数或状况变量的平稳随机分布. 万方数据
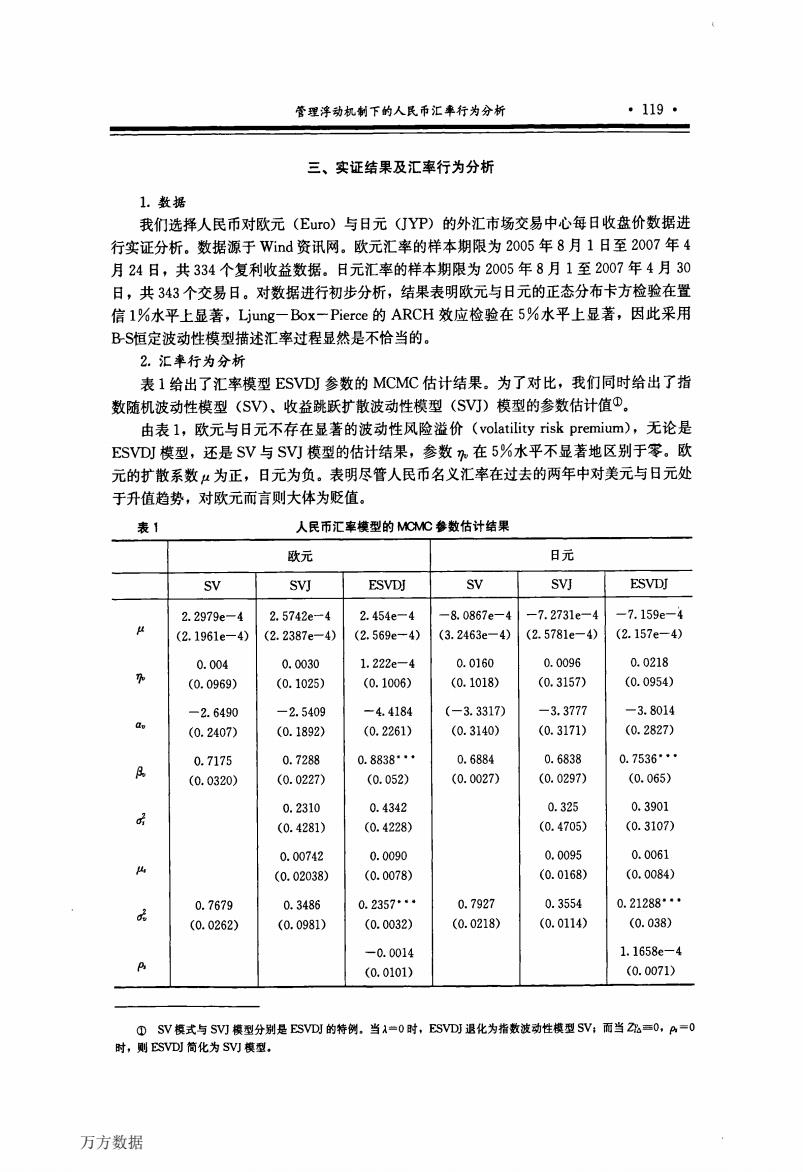
管理浮动机制下的人民币汇率行为分析 ·119· 三、实证结果及汇率行为分析 1.数据 我们选择人民币对欧元(Euro)与日元(JYP)的外汇市场交易中心每日收盘价数据进 行实证分析。数据源于Wind资讯网。欧元汇率的样本期限为2005年8月1日至2007年4 月24日,共334个复利收益数据。日元汇率的样本期限为2005年8月1至2007年4月30 日,共343个交易日。对数据进行初步分析,结果表明欧元与日元的正态分布卡方检验在置 信1%水平上显著,Ljung一Box一Pierce的ARCH效应检验在5%水平上显著,因此采用 BS恒定波动性模型描述汇率过程显然是不恰当的。 2.汇率行为分析 表1给出了汇率模型ESVDJ参数的MCMC估计结果。为了对比,我们同时给出了指 数随机波动性模型(SV)、收益跳跃扩散波动性模型(SV叮)模型的参数估计值①。 由表l,欧元与日元不存在显著的波动性风险溢价(volatility risk premium),无论是 ESVDJ模型,还是SV与SV叮模型的估计结果,参数%在5%水平不显著地区别于零。欧 元的扩散系数μ为正,日元为负。表明尽管人民币名义汇率在过去的两年中对美元与日元处 于升值趋势,对欧元而言则大体为贬值。 表1 人民币汇率模型的MCMC参数估计结果 欧元 日元 SV SVJ ESVDJ SV SVJ ESVDJ 2.2979e-4 2.5742e-4 2.454e-4 -8.0867e-4 -7.2731e-4 -7.159e-4 (2.1961e-4) (2.2387e-4) (2.569e-4) (3.2463e-4) (2.5781e-4) (2.157e-4) 0.004 0.0030 1.222e-4 0.0160 0.0096 0.0218 (0.0969) (0.1025) (0.1006) (0.1018) (0.3157) (0.0954) -2.6490 -2.5409 -4.4184 (-3.3317) -3.3777 -3.8014 (0.2407) (0.1892) (0.2261) (0.3140) (0.3171) (0.2827) 0.7175 0.7288 0.8838· 0.6884 0.6838 0.7536· (0.0320) (0.0227) (0.052) (0.0027) (0.0297) (0.065) 0.2310 0.4342 0.325 0.3901 (0.4281) (0.4228) (0.4705) (0.3107) 0.00742 0.0090 0.0095 0.0061 (0.02038) (0.0078) (0.0168) (0.0084) 0.7679 0.3486 0.2357· 0.7927 0.3554 0.21288· (0.0262) (0.0981) (0.0032) (0.0218) (0.0114) (0.038) -0.0014 1.1658e-4 (0.0101) (0.0071) ①SV模式与SV)模型分别是ESVDJ的特例,当A=0时,ESVDJ退化为指数波动性模型SV;而当2=0,A=0 时,则SVD简化为SV)模型, 万方数据
管理浮动机制下的人民币汇率行为分析 ·119· 三、实证结果及汇率行为分析 1.数据 我们选择人民币对欧元(Euro)与日元(JYP)的外汇市场交易中心每日收盘价数据进 行实证分析。数据源于Wind资讯网。欧元汇率的样本期限为2005年8月1日至2007年4 月24日,共334个复利收益数据。日元汇率的样本期限为2005年8月l至2007年4月30 日,共343个交易日。对数据进行初步分析,结果表明欧元与日元的正态分布卡方检验在置 信1%水平上显著,Ljung—Box—Pierce的ARcH效应检验在5%水平上显著,因此采用 BS恒定波动性模型描述汇率过程显然是不恰当的。 2.汇率行为分析 表1给出了汇率模型ESvD,参数的MCMC估计结果。为了对比,我们同时给出了指 数随机波动性模型(SV)、收益跳跃扩散波动性模型(SⅥ)模型的参数估计值①。 由表1,欧元与日元不存在显著的波动性风险溢价(voIatiIity risk premium),无论是 EsⅧJ模型,还是SV与SvJ模型的估计结果,参数吼在5%水平不显著地区别于零。欧 元的扩散系数肛为正,日元为负。表明尽管人民币名义汇率在过去的两年中对美元与日元处 于升值趋势,对欧元而言则大体为贬值。 表1 人民币汇率模型的M|0MC参数估计结果 欧元 日元 SV SⅥ ESv】讲 SV SⅥ ESⅥW 2.2979e一4 2.5742e一4 2.454e一4 一8.0867e一4 一7.2731e一4 一7.159e一4 p (2.1961e一4) (2.2387e一4) (2.569e一4) (3.2463e一4) (2.5781e一4) (2.157e一4) 0.004 O.0030 1.222e一4 O.0160 O.0096 O.0218 咖 (0.0969) (O.1025) (O.1006) (O.1018) (O.3157) (0.0954) 一2.6490 一2.5409 一4.4184 (一3.3317) 一3.3777 一3.8014 a… (0.2407) (O.1892) (O.2261) (O.3140) (O.3171) (O.2827) O.7175 O.7288 O.8838… O.6884 0.6838 O.7536… 佛 (O.0320) (O.0227) (O.052) (O.0027) (O.0297) (O.065) O.2310 O.4342 O.325 O.3901 彳 (O.4281) (0.4228) (0.4705) (O.3107) O.00742 O.0090 0.0095 O.0061 雎 (0.02038) (O.0078) (O.0168) (O.0084) O.7679 O.3486 O.2357’。。 O.7927 O.3554 O.21288… Z (O.0262) (O.0981) (O.0032) (0.0218) (0.0114) (0.038) 一O.0014 1.1658e一4 B (O.0101) (O.0071) ①SV模式与SⅥ模型分别是ESvDI的特例。当^=O时,ESVDJ退化为指数波动性模型SV;而当Z如一O.D=O 时,则ESVDJ简化为S、,J模型. 万方数据