
上海交通大学随机模拟方法与应用课程论文 上滋充通大粤 随机模拟方法与应用课程论文 论文题目:论文选读 一一基于GA-MCMC的粒子滤波图像恢复算法 学生姓名: 胡卓然 吴迪舟 焦一航 所在院系: 物理与天文系 所在专业: 物理学 所在班级: F1407201 F1407201 F1407202 学生学号: 514072900951407290065140729045 指导教师: 肖柳青 完成时间: 2015年6月 1
上海交通大学随机模拟方法与应用课程论文 1 随机模拟方法与应用课程论文 论文题目: 论文选读——基于GA-MCMC的粒子滤波图像恢复算法 学生姓名: 胡卓然 吴迪舟 焦一航 所在院系: 物理与天文系 所在专业: 物理学 所在班级: F1407201 F1407201 F1407202 学生学号: 5140729009 5140729006 5140729045 指导教师: 肖柳青 完成时间: 2015 年 6 月

上海交通大学随机模拟方法与应用课程论文 目录 摘要 3 1、遗传算法(GA) 3 2、粒子滤波(PF:Particle Filter). 3 2.1概念 3 2.2感性认识 .4 2.3传统的粒子滤波一一贝叶斯滤波.… 5 2.3.1模型 ..5 2.3.2预测过程p(x-Y)→p(x-) ..5 2.3.3更新过程pxY)→p(xY) 6 2.4权重函数 ..6 2.4.1概念… .6 2.4.2权重函数递推.… 2.4.3重要密度函数(qx)的选择. .8 2.5传统的随机模拟方法 3.论文的创新点 8 3.1传统粒子滤波(贝叶斯滤波)的不足 3.2遗传算法与粒子滤波的相似性 8 3.3GA-MCMC粒子重采样… .8 3.3.1重组 ..8 3.3.2变异 .9 3.3.3选择… .9 3.4实验结果及分析 9 4.结论 10 5.自己的看法 .10 2
上海交通大学随机模拟方法与应用课程论文 2 目录 摘要 ...................................................................................................................................... 3 1、遗传算法(GA)..................................................................................................................3 2、粒子滤波(PF: Particle Filter)..................................................................................................3 2.1概念 ................................................................................................................................3 2.2感性认识 ........................................................................................................................4 2.3 传统的粒子滤波——贝叶斯滤波...................................................................................5 2.3.1 模型.............................................................................................................................5 2.3.2 预测过程 1 1 1 ( | ) ( | ) k k k k p x Y p x Y .......................................................................5 2.3.3 更新过程 1 ( | ) ( | ) k k k k p x Y p x Y ............................................................................6 2.4 权重函数 ......................................................................................................................6 2.4.1 概念.............................................................................................................................6 2.4.2 权重函数递推..............................................................................................................7 2.4.3 重要密度函数(qx)的选择.......................................................................................8 2.5传统的随机模拟方法 .....................................................................................................8 3. 论文的创新点 ...................................................................................................................8 3.1传统粒子滤波(贝叶斯滤波)的不足.............................................................................8 3.2 遗传算法与粒子滤波的相似性 ......................................................................................8 3.3GA-MCMC 粒子重采样.......................................................................................................8 3.3.1 重组.............................................................................................................................8 3.3.2 变异.............................................................................................................................9 3.3.3 选择.............................................................................................................................9 3.4 实验结果及分析 ...........................................................................................................9 4. 结论 ..................................................................................................................................10 5. 自己的看法 ......................................................................................................................10

上海交通大学随机模拟方法与应用课程论文 论文选读一一 基于GA-MCMC的粒子滤波图像恢复算法 作者:胡卓然 吴迪舟 焦一航 学号:514072900951407290065140729045 学院:物理与天文系指导教师:肖柳青 摘要 针对粒子滤波的退化和贫化问题,提出一种GA-MCMC粒子滤波图像恢复算法.该算法引 入遗传算法(GA)全局寻优和粒子总数多样性的特性,结合马尔可夫链蒙特卡罗方法(MCMC)的收 敛性,将交叉、变异和选择等操作融人到粒子滤波图像恢复中,提高了粒子滤波的鲁捧性、精 确性和灵活性,实验结果表明,该算法能减少贫化和退化问题,且在对具有混合噪声的真实图 像恢复效果方面显示了其优越性. 关键词:图像恢复:粒子滤波;遗传算法:马尔可夫链蒙特卡洛(MCMC) 1、遗传算法(GA) 遗传算法是模仿生物进化过程中自适应演化的一种优化方法,它也是MCMC思想的一种应 用。该算法产生建议与接受状态的方式比较特殊,其主要方式是将优化问题的所有可行解看作 一群生物个体,对这群个体的基因进行重组、变异、以及选择性复制以繁衍出下一代群体。 遗传算法的三大要素: ·计算机编码方式来表示状态空间 如:固定长度的二进制数位串 父代:10110101010100 母代:10111010 111010 后代:10110101111010 ·定义三种随机算子:变异、重组、选择 ·定义适应度函数 2、粒子滤波(PF:Particle Filter) 2.1概念 粒子滤波的思想基于蒙特卡洛方法(Monte Carlo methods),它是利用粒子集来表示概率,可 以用在任何形式的状态空间模型上。其核心思想是通过从后验概率中抽取的随机状态粒子来表 达其分布,是一种顺序重要性采样法(Sequential Importance Sampling)。简单来说,粒子滤波法 是指通过寻找一组在状态空间传播的随机样本对概率密度函数进行近似,以样本均值代替积分 运算,从而获得状态最小方差分布的过程。这里的样本即指粒子,当样本数量N→∝时可以逼近 任何形式的概率密度分布。 ·本身就是随机模拟过程 2.2感性认识
上海交通大学随机模拟方法与应用课程论文 3 论文选读——基于GA-MCMC的粒子滤波图像恢复算法 作者:胡卓然 吴迪舟 焦一航 学号:5140729009 5140729006 5140729045 学院:物理与天文系 指导教师:肖柳青 摘要 针对粒子滤波的退化和贫化问题,提出一种 GA-MCMC 粒子滤波图像恢复算法.该算法引 入遗传算法(GA)全局寻优和粒子总数多样性的特性,结合马尔可夫链蒙特卡罗方法(MCMC)的收 敛性,将交叉、变异和选择等操作融人到粒子滤波图像恢复中,提高了粒子滤波的鲁捧性、精 确性和灵活性.实验结果表明,该算法能减少贫化和退化问题,且在对具有混合噪声的真实图 像恢复效果方面显示了其优越性. 关键词:图像恢复;粒子滤波;遗传算法;马尔可夫链蒙特卡洛(MCMC) 1、遗传算法(GA) 遗传算法是模仿生物进化过程中自适应演化的一种优化方法,它也是 MCMC 思想的一种应 用。该算法产生建议与接受状态的方式比较特殊,其主要方式是将优化问题的所有可行解看作 一群生物个体,对这群个体的基因进行重组、变异、以及选择性复制以繁衍出下一代群体。 遗传算法的三大要素: •计算机编码方式来表示状态空间 如:固定长度的二进制数位串 父代:10110101 010100 母代:10111010 111010 后代:10110101 111010 •定义三种随机算子:变异、重组、选择 •定义适应度函数 2、粒子滤波(PF: Particle Filter) 2.1 概念 粒子滤波的思想基于蒙特卡洛方法(Monte Carlo methods),它是利用粒子集来表示概率,可 以用在任何形式的状态空间模型上。其核心思想是通过从后验概率中抽取的随机状态粒子来表 达其分布,是一种顺序重要性采样法(Sequential Importance Sampling)。简单来说,粒子滤波法 是指通过寻找一组在状态空间传播的随机样本对概率密度函数进行近似,以样本均值代替积分 运算,从而获得状态最小方差分布的过程。这里的样本即指粒子,当样本数量 N→∝时可以逼近 任何形式的概率密度分布。 •本身就是随机模拟过程 2.2 感性认识
上海交通大学随机模拟方法与应用课程论文 p(x,IZ,) P(IX) {9,Ww qg,lx4)t 承采样 .VNE ?,w哈 P(xIZ) vL X 上图分为三层,每层分别代表粒子滤波一个循环中的三个重要步骤。在第一层,默认每种 粒子的重要性相同,均为1/N,曲线的峰值代表该粒子出现的几率较大。然而,事实上每种粒 子的重要性并不相同,其中所谓的的重要性极低,是对整体样本起干扰作用的,我们的理想状 态是把所谓的“噪声粒子”从整体样本中挑选出来。 因而,在第二层一一重采样过程,某些重要性较大的具有样本代表性的粒子被挑选出来, 并按照其重要性大小(权重函数w)将粒子不同程度的放大(复制样本)。 第三层,重采样过程得到的粒子又有了相同的重要性,得到某种粒子出现的后验概率。 如此经过N趋向于无穷次的循环,我们不妨将N次循环后的粒子出现的概率视为剔除“噪 声粒子”后粒子的实际分布 以上为传统意义的粒子滤波过程,而本文的创新点在于将GA-MCMC方法应用到重采样过 程。即重采样过程不再是简单的复制重要性大的样本,而是将重要性大的样本作为父本,经过 变异、重组、选择三种算子变换后得到的子代,再对子代进行下一次循环。 23传统的粒子滤波模型一一贝叶斯滤波 2.3.1模型
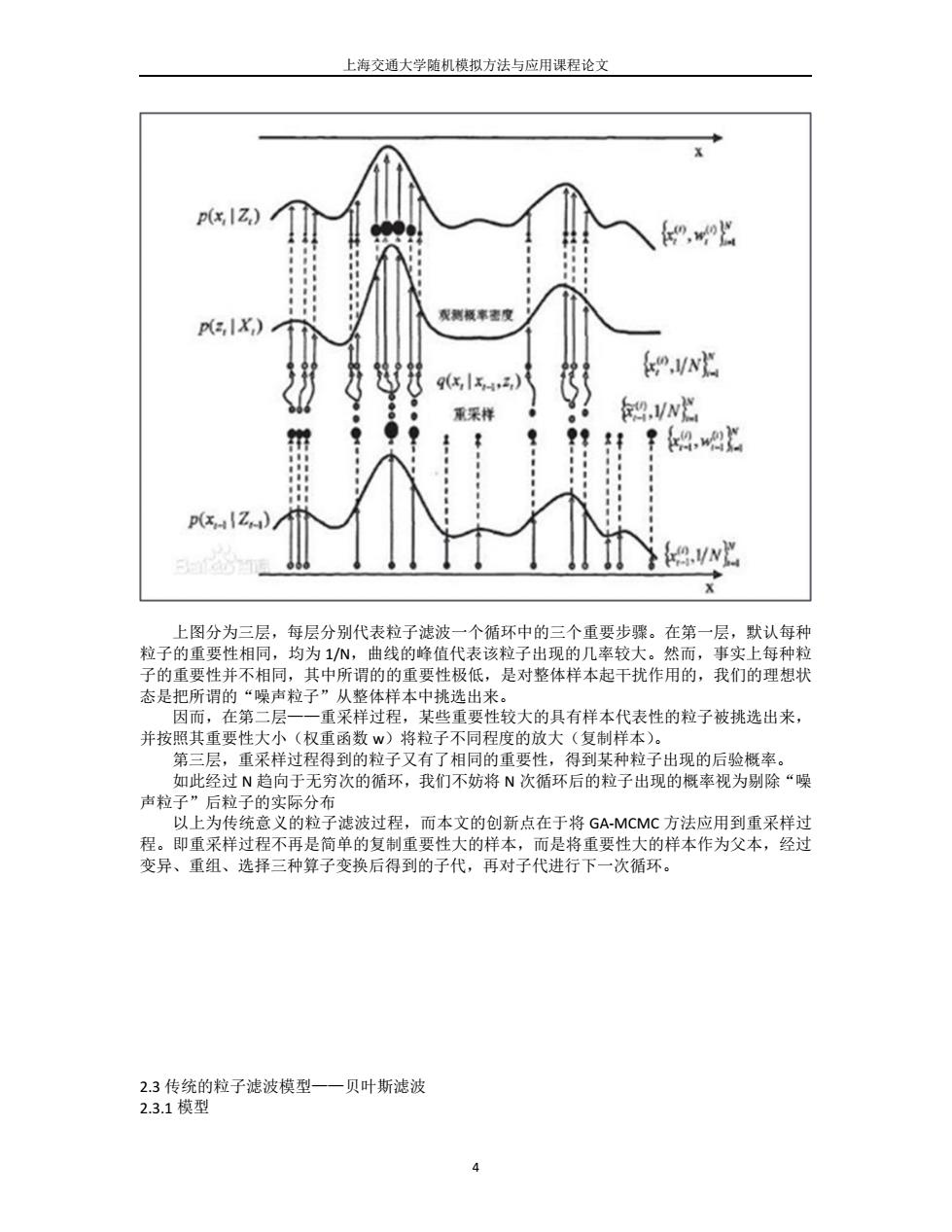
上海交通大学随机模拟方法与应用课程论文 4 上图分为三层,每层分别代表粒子滤波一个循环中的三个重要步骤。在第一层,默认每种 粒子的重要性相同,均为 1/N,曲线的峰值代表该粒子出现的几率较大。然而,事实上每种粒 子的重要性并不相同,其中所谓的的重要性极低,是对整体样本起干扰作用的,我们的理想状 态是把所谓的“噪声粒子”从整体样本中挑选出来。 因而,在第二层——重采样过程,某些重要性较大的具有样本代表性的粒子被挑选出来, 并按照其重要性大小(权重函数 w)将粒子不同程度的放大(复制样本)。 第三层,重采样过程得到的粒子又有了相同的重要性,得到某种粒子出现的后验概率。 如此经过 N 趋向于无穷次的循环,我们不妨将 N 次循环后的粒子出现的概率视为剔除“噪 声粒子”后粒子的实际分布 以上为传统意义的粒子滤波过程,而本文的创新点在于将 GA-MCMC 方法应用到重采样过 程。即重采样过程不再是简单的复制重要性大的样本,而是将重要性大的样本作为父本,经过 变异、重组、选择三种算子变换后得到的子代,再对子代进行下一次循环。 2.3 传统的粒子滤波模型——贝叶斯滤波 2.3.1 模型

上海交通大学随机模拟方法与应用课程论文 p(yx:) 2 p(xx:-1) 图2.1状态空间模型 在目标跟踪问题中,动态系统的状态空间模型可描述为 x,=f(x-)+“-1 (2.1) =h()+v 其中∫(),()分别为状态转移方程与观测方程,x,为系统状态,y,为观测值,“,为过程 噪声,y,为观测噪声,为了描述方便,用X,=x1=代。,…,x}与Y=八u={,,》} 分别表示0到k时刻所有的状态与观测值。在处理目标跟踪问题时,通常假设目标的状态转 移过程服从一阶马尔可夫模型,即当前时刻的状态x,只与上一时刻的状态x,有关。另外 一个假设为观测值相互独立,即观测值y,只与k时刻的状态x,有关。 2.32预测过程p(x-Y)→p(xY-) 假设已知k-1时刻的概率密度函数为p(x-11Y-),贝叶斯滤波的具体过程如下: (1)预测过程,由p(x-1IY-)得到p(x1Y-) P(x,x-1Y-)=p(x|x-1Y-)P(x-1IY-) 当给定x,时,状态x与Y-相互独立,因此 p(x,x1lY)=p(1-)p(-Y-) 上式两端对x-,积分,可得Chapman-Komolgorov方程 p(x)=[p(xx)p(xY)dx 2.33更新过程px|Y-)→p(xY) 5
上海交通大学随机模拟方法与应用课程论文 5 2.3.2 预测过程 1 1 1 ( | ) ( | ) k k k k p x Y p x Y 2.3.3 更新过程 1 ( | ) ( | ) k k k k p x Y p x Y