
水 利 学 报 2007年12月 SHUILI XUEBAO 第38卷第12期 文章编号:0559-9350(2007)12.1500-07 基于AM-MCMC算法的贝叶斯概率洪水预报模型 邢贞相,芮孝芳2,崔海燕,余美2 (1.东北农业大学水利与建筑学院,黑龙江哈尔滨150030:2.河海大学水文水资源学院,江苏南京210098) 摘要:本文在贝叶斯预报系统的框架下,利用B即网络能描述非线性映射的特性建立了基于BP网络的先验密度和 似然函数的模型,并采用基于自适应采样算法(Adaptive Metropolis algorithm,简称AM)的马尔可夫链蒙特卡罗模拟方 法(Markov Chain Monte Carlo,.简称MCMC)求解流量的后验密度,最后给出流量的概率预报。实例表明,恭于AM- MCMC的BP贝叶斯概率水文预报的精度高,且能给出预报的方差,使得防洪决策可以考虑预报的不确定性。 关键词:贝叶斯预报系统;自适应;MCMC:城率预报 中图分类号:338 文献标识码:A 现行水文预报模型大多是确定性的。实际上,模型的输人、模型的结构和参数均是不确定的,故模 型输出的预报值也是不确定性的。统计决策理论指出,根据不确定的水文预报做决策时,如果不考虑它 的不确定度,则从期望意义上讲,决策中的价值不一定是非负的,只有在考虑了预报不确定度的决策中, 水文预报的价值才始终是正的1,2l。Krzysztofowicz3-91提出的贝叶斯概率预报系统(Bayesian Forecasting System,简称BFS)是通过确定性水文模型进行概率预报解决水文预报不确定性的一个理论框架。黄伟 军提出灰色模糊贝叶斯的概念,建议贝叶斯模型的先验分布采用灰色先验、似然函数采用模糊似然 函数。张洪刚建议采用平稳序列线性AR模型与线性扰动模型(LPM)分别描述先验分布与似然函 数,在一定程序上降低了贝叶斯求解的复杂度。李向阳等采用神经网络模型来描述先验分布与似然 函数,进一步降低了贝叶斯求解过程的复杂度。Krzysztofowicz提出的BS,需要对流量实测值和确定性 水文模型的预报值进行亚高斯转换及线性正态假设来获取先验密度与函数的非线性关系,再采用线性 回归求解转换空间的后验密度,然后将其转换为原始空间的后验密度[。该法计算的复杂性和线性正 态假设大大影响了其适用性。为此,文献[1]利用神经网络的非线性映射能力来描述贝叶斯先验密度与 似然函数,并对湖南双牌水库的洪水预报进行了实例验证。但其中两点不足:(1)神经的性能很大程度 上与初始的权值和厨值有关,常出现网络的收敛速度很慢甚至不收敛的情况。(2)Metropolis-Hasting算 法必须预先根据经验确定参数的抽样区间和推荐分布,难以保证参数的各态遍历性和算法的快速收敛。 本文提出应用基于自适应算法的马尔可夫蒙特卡罗模拟和基于遗传算法的B神经网络来研究流域出 口新面流量的概率预报。采用加速遗传算法优化神经网络的初始权值和國值,可使BP网络很快地收 敛:基于自适应算法的马尔可夫链蒙特卡罗模拟不再依赖于参数的推荐分布,也不受参数的先验区 间的影响,能够保证算法的遍历性和较高的抽样效率。 1贝叶斯概率预报原理 假设流域出口流量过程为p阶马尔可夫过程。令Q。Q,Q-1,…,Q-+1{为在预报时刻t已知的 收稿日期:2007-0130 基金项目:回家自然科学基金资助项目(50309002) 作者简介:邢贞相(1976-),男,黑龙江讷河人,博士,主要从事随机水文预报、水资趣系统优化等方面的研究。 E-mail xingzhenxiango1 @163.com -1500 万方数据
2007年12月 水 利 学 报 SHUIU XUEBAO 第38卷 第12期 文章编号:0559—9350(2007)12一1500—07 基于AM.MCMC算法的贝叶斯概率洪水预报模型 邢贞相1,芮孝芳2,崔海燕1,余 美2 (1.东北农业大学水利与建筑学院,黑龙江哈尔滨 150030;2.河海大学水文水资源学院,江苏南京210098) 摘要:本文在贝叶斯预报系统的框架下,利用BP网络能描述非线性映射的特性建立了基于BP网络的先验密度和 似然函数的模型。并采用基于自适应采样算法(Ad印tive Metropolis algorithm,简称AM)的马尔可夫链蒙特卡罗模拟方 法(Markov chain Monte carlo,简称McMc)求解流量的后验密度,最后给出流量的概率预报。实例表明,基于AM— McMc的BP贝叶斯概率水文预报的精度高,且能给出预报的方差,使得防洪决策可以考虑预报的不确定性。 关键词:贝叶斯预报系统;自适应;McMc;概率预报 中图分类号:P338 文献标识码:A 现行水文预报模型大多是确定性的。实际上,模型的输入、模型的结构和参数均是不确定的,故模 型输出的预报值也是不确定性的。统计决策理论指出,根据不确定的水文预报做决策时,如果不考虑它 的不确定度,则从期望意义上讲,决策中的价值不一定是非负的,只有在考虑了预报不确定度的决策中, 水文预报的价值才始终是正的¨卫J。Krzysztofowicz∞棚1提出的贝叶斯概率预报系统(Bayesiall Fo『ecasting svstem,简称BFs)是通过确定性水文模型进行概率预报解决水文预报不确定性的一个理论框架。黄伟 军【1 0。提出灰色模糊贝叶斯的概念,建议贝叶斯模型的先验分布采用灰色先验、似然函数采用模糊似然 函数。张洪刚¨¨建议采用平稳序歹{j线性AR模型与线性扰动模型(LPM)分别描述先验分布与似然函 数,在一定程序上降低了贝叶斯求解的复杂度。李向阳等¨2。采用神经网络模型来描述先验分布与似然 函数,进一步降低了贝叶斯求解过程的复杂度。Krzysztof0诵cz提出的BFS,需要对流量实测值和确定性 水文模型的预报值进行亚高斯转换及线性正态假设来获取先验密度与函数的菲线性关系,再采用线性 回归求解转换空间的后验密度,然后将其转换为原始空间的后验密度№1。该法计算的复杂性和线性正 态假设大大影响了其适用性。为此,文献[1]利用神经网络的非线性映射能力来描述贝叶斯先验密度与 似然函数,并对湖南双牌水库的洪水预报进行了实例验证。但其中两点不足:(1)神经的性能很大程度 上与初始的权值和阈值有关,常出现网络的收敛速度很慢甚至不收敛的情况。(2)Metropolis.Hausting算 法必须预先根据经验确定参数的抽样区间和推荐分布,难以保证参数的各态遍历性和算法的快速收敛。 本文提出应用基于自适应算法的马尔可夫蒙特卡罗模拟和基于遗传算法的BP神经网络来研究流域出 口断面流量的概率预报。采用加速遗传算法优化神经网络的初始权值和阈值,可使BP网络很快地收 敛n4 o;基于自适应算法的马尔可夫链蒙特卡罗模拟不再依赖于参数的推荐分布,也不受参数的先验区 间的影响,能够保证算法的遍历性和较高的抽样效率。 l 贝叶斯概率预报原理 但设流域出口流量过程为p阶马尔可夫过程。令Q。{QI,Q。,… ,Q。。+。}为在预报时刻£已知的 收藕日期:2007.01.30 基金项目:国家自然科学基金资助项目(50309002) 作者简介:邢贞相(1976一)。男,黑龙江讷河人,博士,主要从事随机水文预报、水资源系统优化等方面的研究。 E-mIl:xi“gzhe眦iarl90l@163.com 一1500— 万方数据

前期流量过程:Q。为待预报的流量过程,n=1,2,…,N:S。为确定性水文模型的输出流量过程,n=1, 2,…N;9o、9.、3n分别为水文变量Q。、Q。、S.的实现值;n为预见期。 根据贝叶斯公式,可求出实际流量q。的后验密度): (g.15.,9)=5199)g(g。19o) f(5n19a·90)g(q.19o) (1) L(sI go) f(s.I 9.,90)g(q.I go)dq 式中:(q.I5n,9o)为gn的后验密度;g(9nI90)为q。的先验密度,只与qo有关,在预报时刻为已知; f(snIq,qo)为s,已知时q。的似然函数,反映确定性水文模型的预报能力。 式(1)中的流量先验密度和似然函数采用BP网络结构确定2: 流量先验密度的BP网络结构可表示为 Q。=G(Q.1Q。)+Ξ (2) 式中:G为流量先验密度的非线性映射:三。为残差,假设服从正态分布N(0,),其中:为三。,的均方 差:其余符号的意义同前述。 流量先验密度一般采用只有一个隐层的神经网络结构(图1)。由式(2)可知 E(Q。1Q。=qa)=G(qa) (3) Var(Q。lQo=qa)=e2 (4) 因此,流量先验密度用下列正态分布表示: g(g.1q)=2e 2e2 (5) 流量似然函数的BP网络结构可表示为 S。=F(S.1q.,qo)+⊙。 (6) 式中:F为似然函数的BP网络非线性映射;日。为残差,假设服从正态分布W(0,),其中0为⊙,的均 方差。 流量似然函数一般也采用只有一个隐层的神经网络结构(图2)。由式(6)可知 E(Sn1Q。=9,Q。=9o)=F(qa,qo) (7) ar(S。lQ.=9.,Q。=9o)=g2 (8) 因此,流量似然函数可用下列正态分布表示: 1 f1g9)=/2x0p- _(s。-F(g。,9o)2 (9) 202 将所建立的流量先验密度g(q.|qa)和似然密度f(sn|q。,9o)代入式(1)即可求解流量后验密度 中(9.15。,90)。但由于无法获得q。的具体取值区间以求出归一化常数l,故很难求得最终解析解。为此, 本文采用自适应马尔可大链蒙特卡罗(AM-MCMC)算法来解决。 2AM-MCMC算法 作为随机模拟方法的马尔可夫链蒙特卡罗(MCMC)方法早已被许多学者应用到物理、天文、气象、 通信等方面5-。MCMC的关键是如何选择推荐分布(转移密度)使采样更加有效。常用的采样方法 有Metropolis--Hastings.i6算法、吉布斯(Gibbs)采样)和Adapative Metropolis(AM)算法1。这3种方法 中只有AM算法不依赖于事先确定的推荐分布且收敛速度快,故本文采用此算法。 2.1AM算法AM(Adaptive Metropolis)算法是Haafio于2O01年提出的一种改进的MCMC采样器。相 比传统的M-H与Gibbs采样,AM不再需要事先确定变量的推荐分布,而是决定于初始抽样的协方差。 将推荐分布定义为参数空间的多维正态分布形式,其初始协方差可根据先验信息确定。在抽样过程中 根据马尔可夫链的历史抽样信息自适应的调整椎荐密度(即协方差矩阵),且可并行运算,提高了算法的 -1501- 万方数据
万方数据

收敛速度。 9n 9o-pl 输入层 隐层 输出层 输入层 隐层 输出层 图1先验密度的BP网络结构 图2似然函数的BP网络结构 设t时刻已经抽取样本g°,g,…,91,根据这些历史得到推荐分布q,(·1g°,g,…,g)生成新的 样本g,根据式(10)计算的接受概率来判断是否接受该新样本: a(',-)min1, ,」,fs.19,9o)g(919o)1 1”fs.1q,9o)g(gn1qo) (10) AM算法将推荐分布g,(1g°,g',…,9)定义为以9-1为均值,Com(g°,q',…,g-)为协方差的正 态分布。协方差的计算如式(11)所示。在初始抽样次数i≤°中,协方差C:取固定值C。(C。的确定可 根据先验确定),之后自适应更新。 「Co i≤to C.Cou())sit (11) 式中:ε为一个较小的正数,以确保C:不为奇异矩阵;s:为一个比例因子,依赖于变量的维数d,以确保 接受概率在一个合适的范围内,Gelman等9建议s:取为2.41d;I,为d维单位矩阵。to为初始抽样次 数。 第:+1次迭代的协方差根据式(11)计算得出,即式(12)所示: C=:c+(项9-(i+10g+9g+) (12) 式中:q:-,和9:为前i-1次和i次抽样的均值;9为向量q:的转置。 由上可知,AM算法的采样机制与所有的历史样本信息qo,q,…,9-1有关,Haario等1证明了该算 法的收敛性及遍历性。AM算法的具体采样步骤如下:(1)初始化,i=0;(2)初始状态q:在其变量的先 验范围内随机产生并接受;①利用式(11)计算协方差C:;②产生推荐变量q'~N(9:,C:):③按式(10) 计算接受概率a;④产生一个均匀随机数u~U(0,1);⑤若u<a,接受q:+1=g”,否则q1=9:;(3)i= i+1,重复①~⑤直至产生预先要求的样本数量为止。 2.2收敛判断准则MCMC研究的一个重要任务是判断并行采样序列是否收敛到后验分布。理论上 一个各向同性的采样器在t→o时一定收敛,而在实际应用中并非如此。Geman等o提出了一种定量 的比例缩小得分(scale reduction score)√R用以诊断收敛性,得到了广泛应用。计算方法如下: =√+语 (13) B1i=∑(4-)子(k-1) (14) W=∑s1k (15) 式中:i为每次并行运算的抽样次数;k为并行采样的次数;B/i为各次并行运算样本均值u的方差;ū 为4的均值。W为各次并行运算样本方差s的均值:通常,比例缩小得分接近1则表示算法达到收敛。 -1502- 万方数据
万方数据
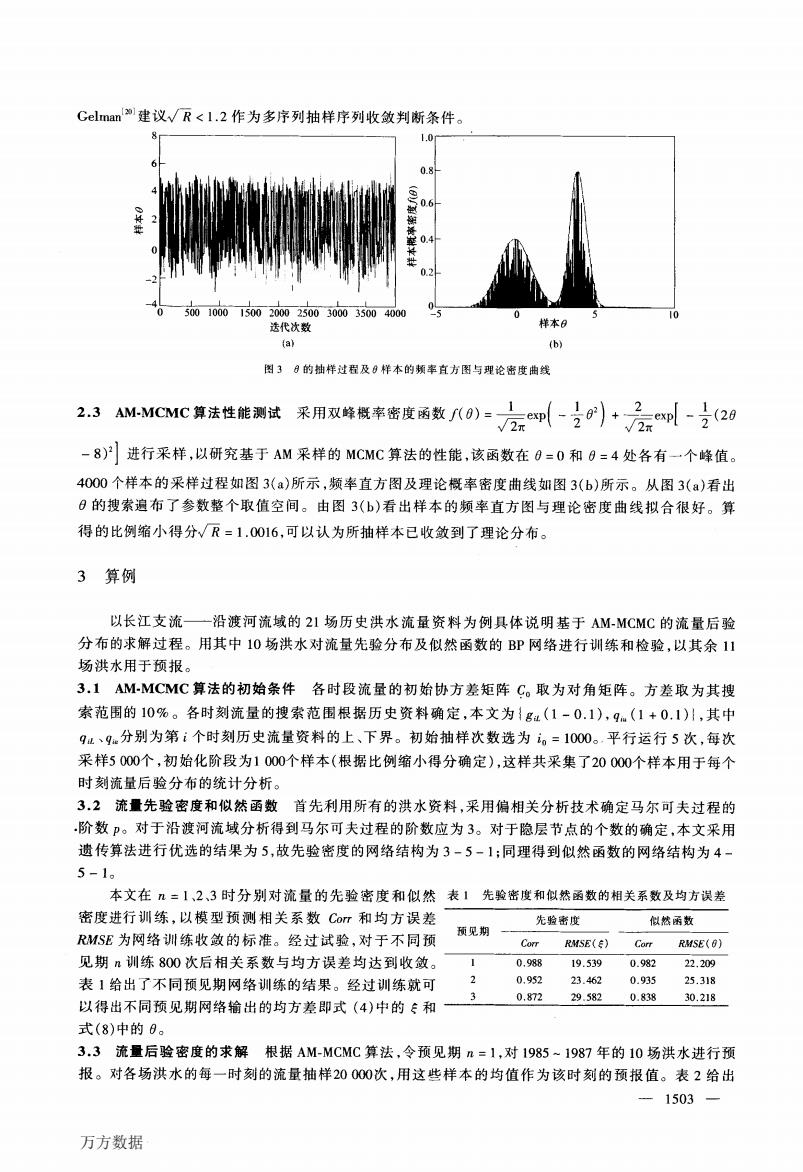
Gelman建议√R<l.2作为多序列抽样序列收敛判断条件。 1.0 0.2 0.2 5001000150020002500300035004000 0 选代次数 样本8 (a) (b) 图3日的轴样过程及8样本的频率直方图与理论密度曲线 2.3 AM-MCMC算法性能测试采用双峰概率密度函数/八0)=方即-0)小+云-之20 2元 -8)2进行采样,以研究基于AM采样的MCMC算法的性能,该函数在0=0和0=4处各有一个峰值。 4000个样本的采样过程如图3(a)所示,频率直方图及理论概率密度曲线如图3(b)所示。从图3(a)看出 日的搜索遍布了参数整个取值空间。由图3(b)看出样本的频率直方图与理论密度曲线拟合很好。算 得的比例缩小得分√R=1.0016,可以认为所抽样本已收敛到了理论分布。 3算例 以长江支流一沿渡河流域的21场历史洪水流量资料为例具体说明基于AM-MCMC的流量后验 分布的求解过程。用其中10场洪水对流量先验分布及似然函数的BP网络进行训练和检验,以其余11 场洪水用于预报。 3.1AM-MCMC算法的初始条件各时段流量的初始协方差矩阵C。取为对角矩阵。方差取为其搜 索范围的10%。各时刻流量的搜索范围根据历史资料确定,本文为{g1(1-0.1),q(1+0.1)川,其中 9L、9分别为第i个时刻历史流量资料的上、下界。初始抽样次数选为i。=1000。平行运行5次,每次 采样5000个,初始化阶段为1000个样本(根据比例缩小得分确定),这样共采集了20000个样本用于每个 时刻流量后验分布的统计分析。 3.2流量先验密度和似然函数首先利用所有的洪水资料,采用偏相关分析技术确定马尔可夫过程的 阶数。对于沿渡河流域分析得到马尔可夫过程的阶数应为3。对于隐层节点的个数的确定,本文采用 遗传算法进行优选的结果为5,故先验密度的网络结构为3-5-1:同理得到似然函数的网络结构为4- 5-1。 本文在n=1、2、3时分别对流量的先验密度和似然表1先验密度和似然函数的相关系数及均方误差 密度进行训练,以模型预测相关系数Com和均方误差 先验密度 似然函数 预见期 RMSE为网络训练收敛的标准。经过试验,对于不同预 Corr RMSE() Corr RMSE(0) 见期n训练800次后相关系数与均方误差均达到收敛。 0,988 19.539 0.982 22.209 表1给出了不同预见期网络训练的结果。经过训练就可 2 0.952 23.462 0.935 25.318 3 0.872 29.5820.838 30.218 以得出不同预见期网络输出的均方差即式(4)中的:和 式(8)中的0。 3.3流量后验密度的求解根据AM-MCMC算法,令预见期n=1,对1985~1987年的10场洪水进行预 报。对各场洪水的每一时刻的流量抽样20000次,用这些样本的均值作为该时刻的预报值。表2给出 -1503— 万方数据
万方数据
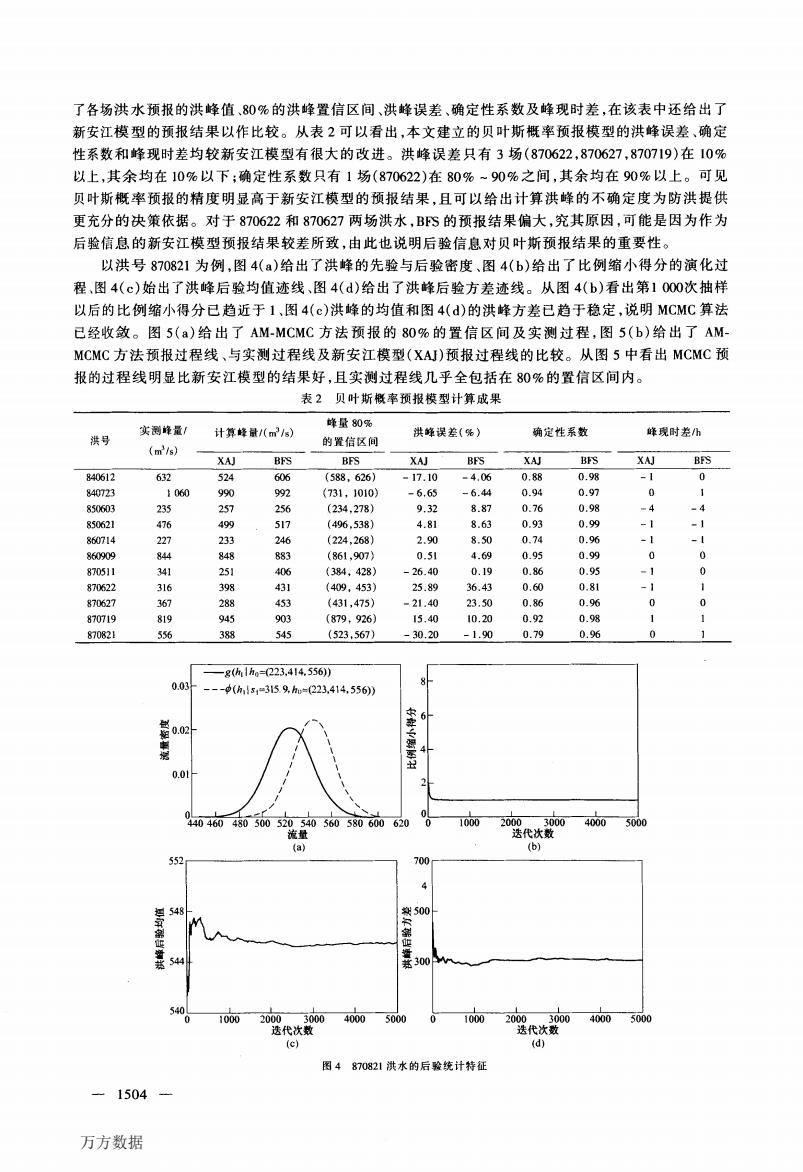
了各场洪水预报的洪峰值、80%的洪峰置信区间、洪蜂误差、确定性系数及峰现时差,在该表中还给出了 新安江模型的预报结果以作比较。从表2可以看出,本文建立的贝叶斯概率预报模型的洪峰误差、确定 性系数和峰现时差均较新安江模型有很大的改进。洪峰误差只有3场(870622,870627,870719)在10% 以上,其余均在10%以下;确定性系数只有1场(870622)在80%~90%之间,其余均在90%以上。可见 贝叶斯概率预报的精度明显高于新安江模型的预报结果,且可以给出计算洪峰的不确定度为防洪提供 更充分的决策依据。对于870622和870627两场洪水,BFS的预报结果偏大,究其原因,可能是因为作为 后验信息的新安江模型预报结果较差所致,由此也说明后验信息对贝叶斯预报结果的重要性。 以洪号870821为例,图4(a)给出了洪峰的先验与后验密度、图4(b)给出了比例缩小得分的演化过 程,图4(c)始出了洪峰后验均值迹线,图4(d)给出了洪峰后验方差迹线。从图4(b)看出第1000次抽样 以后的比例缩小得分已趋近于1、图4(c)洪峰的均值和图4()的洪峰方差已趋于稳定,说明MCMC算法 已经收敛。图5(a)给出了AM-MCMC方法预报的80%的置信区间及实测过程,图5(b)给出了AM- MCMC方法预报过程线、与实测过程线及新安江模型(XA)预报过程线的比较。从图5中看出MCMC预 报的过程线明显比新安江模型的结果好,且实测过程线几乎全包括在80%的置信区间内。 表2贝叶斯概率预报模型计算成果 实测峰量/ 峰量80% 计算峰量(m/s) 洪蜂误差(%》 确定性系数 峰现时差h 洪号 的置信区间 (m/s) XAJ BFS BFS XAJ BFS XAJ BFS XAJ BFS 840612 632 524 606 (588,626) -17.10 -4,06 0.88 0.98 -1 0 840723 1060 990 992 (731,1010) -6.65 -6.44 0.94 0.97 0 850603 235 257 256 (234,278) 9.32 8.87 0.76 0.98 -4 -4 850621 476 499 517 (496.538) 4.81 8.63 0.93 0.99 -1 -1 860714 227 233 246 (224,268) 2.90 8.50 0.74 0.96 -1 -1 860909 844 848 883 (861,907) 0.51 4.69 0.95 0.99 0 0 870511 341 251 406 (384,428) -26.40 0.19 0.86 0.95 -1 0 870622 316 398 431 (409,453) 25.89 36.43 0.60 0.81 -1 870627 367 288 453 (431,475) -21.40 23.50 0.86 0.96 0 0 870719 819 945 903 (879,926) 15.40 10.20 0.92 0.98 1 870821 556 388 545 (523,567) -30.20 -1.90 0.79 0.96 -g(h1h=223,414.556) 0.03 中(h5s1=3引5.9he=223,414,556)》 0.02 0.0 440460480500520540560580600620 10002000300040005000 流量 迭代次数 (a) (6) 552 700 4 548 500 544 基300 540 10002000300040005000 0 10002000300040005000 选代次数 选代次数 (e) (d) 图4870821洪水的后验统计特征 1504.- 万方数据
了各场洪水预报的洪峰值、80%的洪峰置信区间、洪峰误差、确定性系数及峰现时差,在该表中还给出了 新安江模型的预报结果以作比较。从表2可以看出,本文建立的贝叶斯概率预报模型的洪峰误差、确定 性系数和峰现时差均较新安江模型有很大的改进。洪峰误差只有3场(870622,870627,870719)在10% 以上,其余均在10%以下;确定性系数只有1场(870622)在80%~90%之间,其余均在90%以上。可见 贝叶斯概率预报的精度明显高于新安江模型的预报结果,且可以给出计算洪峰的不确定度为防洪提供 更充分的决策依据。对于870622和870627两场洪水,BFS的预报结果偏大,究其原因,可能是因为作为 后验信息的新安江模型预报结果较差所致,由此也说明后验信息对贝叶斯预报结果的重要性。 以洪号870821为例,图4(a)给出了洪峰的先验与后验密度、图4(b)给出了比例缩小得分的演化过 程、图4(C)始出了洪峰后验均值迹线、图4(d)给出了洪峰后验方差迹线。从图4(b)看出第1 000次抽样 以后的比例缩小得分已趋近于1、图4(e)洪峰的均值和图4(d)的洪峰方差已趋于稳定,说明MCMC算法 已经收敛。图5(a)给出了AM.MCMC方法预报的80%的置信区间及实测过程,图5(b)给出了AM. MCMC方法预报过程线、与实测过程线及新安江模型(xAJ)预报过程线的比较。从图5中看出MCMC预 报的过程线明显比新安江模型的结果好,且实测过程线几乎全包括在80%的置信区间内。 表2贝叶斯概率预报模型计算成果 越 船 删 避 迥 睿 裂 妲 登 糍 一1504一 图4 870821洪水的后验统计特征 万方数据