
然而,对X取一阶差分(first difference) △X=Xt-Xt-1Ft 由于μ是一个白噪声,则序列{X+}是平稳的。 后面将会看到:如果一个时间序列是非平稳的, 它常常可通过取差分的方法而形成平稳序列。 ·事实上,随机游走过程是下面我们称之为1阶自回 归AR(1)过程的特例 X:-oXt-1+ut 不难验证:1)中>1时,该随机过程生成的时间序列是 发散的,表现为持续上升(Φ>1)或持续下降(<-1), 因此是非平稳的;
21 • 然而,对X取一阶差分(first difference): Xt=Xt-Xt-1=t 由于t是一个白噪声,则序列{Xt }是平稳的。 后面将会看到:如果一个时间序列是非平稳的, 它常常可通过取差分的方法而形成平稳序列。 • 事实上,随机游走过程是下面我们称之为1阶自回 归AR(1)过程的特例 Xt =Xt-1+t 不难验证:1)||>1时,该随机过程生成的时间序列是 发散的,表现为持续上升(>1)或持续下降(<-1), 因此是非平稳的;

2)=1时,是一个随机游走过程,也是非平 第二节中将证明:只有当-1<<1时,该随机过 才是平稳的。 ·1阶自回归过程AR(1)又是如下k阶自回归AR(K过 程的特例: X=φ1Xt-1tφ2Xt-2.+φxXt-k 该随机过程平稳性条件将在第二节中介绍
22 第二节中将证明:只有当-1<<1时,该随机过程 才是平稳的。 2)=1时,是一个随机游走过程,也是非平稳的。 • 1阶自回归过程AR(1)又是如下k阶自回归AR(K)过 程的特例: Xt = 1Xt-1+2Xt-2.+kXt-k 该随机过程平稳性条件将在第二节中介绍

三、平稳性检验的图示判断 时序图检验: •根据平稳时间序列均值、方差为常数 的性质,平稳序列的时序图应该显示出 该序列始终在一个常数值附近随机波动, 而且波动的范围有界、无明显趋势及周 期特征。 ·自相关图检验: ·平稳序列通常具有短期相关性。该性 质用自相关系数来描述就是随着延迟期 数的增加,平稳序列的自相关系数会很 快地衰减向零。 23
23 三、平稳性检验的图示判断 •时序图检验 : •根据平稳时间序列均值、方差为常数 的性质,平稳序列的时序图应该显示出 该序列始终在一个常数值附近随机波动, 而且波动的范围有界、无明显趋势及周 期特征。 •自相关图检验: •平稳序列通常具有短期相关性。该性 质用自相关系数来描述就是随着延迟期 数的增加,平稳序列的自相关系数会很 快地衰减向零

。1 给出一个随机时间序列,首先可通过该 序列的时间路径图来粗略地判断它是否 是平稳的。 一个平稳的时间序列在图形上往往表现 出一种围绕其均值不断波动的过程; 而非平稳序列则往往表现出在不同的时 间段具有不同的均值(如持续上升或持 续下降)。 24
24 • 给出一个随机时间序列,首先可通过该 序列的时间路径图来粗略地判断它是否 是平稳的。 • 一个平稳的时间序列在图形上往往表现 出一种围绕其均值不断波动的过程; • 而非平稳序列则往往表现出在不同的时 间段具有不同的均值(如持续上升或持 续下降)
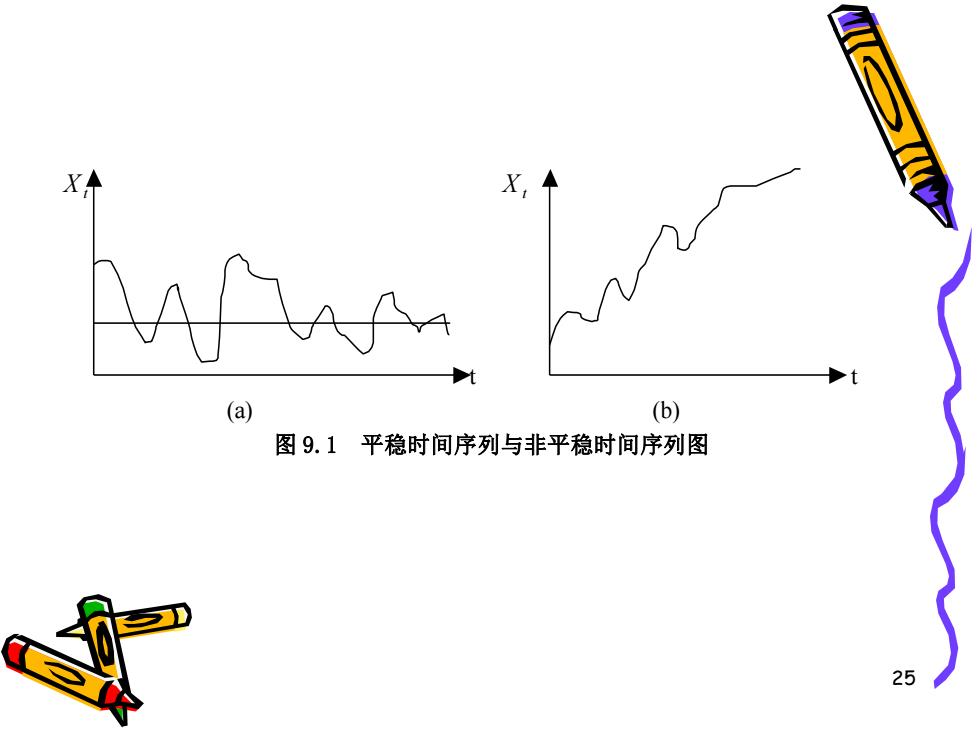
(a (b) 图9.1平稳时间序列与非平稳时间序列图 25
25 X t Xt t t (a) (b) 图 9.1 平稳时间序列与非平稳时间序列图