
特殊地有mf(x)=clmf(x)=cA(c为常数)· 品台 (B≠0) 注:应注重法则的前提条件,若前提条件不满足,则法则失效 正确解法:织x如=0, 又如:mW+左-)≠m+左-m反 :产 limcosx ,是错误的写法,因为B=1mx=0. 1.3.2极限的计算方法 1、直接代入法:即mfx)=fx,) 州1 欧 以下各例都无法直接应用法则,需适当的化简后再应用(应清楚每一步求法的根据), 2、(分型:求解的方法是分子和分母同时约去使分母为0的式子.常用的方法有: 因式分解法提取公因式法分子成分母有理化法一。1(下节介留。 r2+r 例2m2x2+x- 格赋-22-号 x(x+1) 3x2+2x 例3期2x+-x 期限式=里新2-2 6
6 特殊地有 lim ( ) ? cf x x→ = c lim ( ) ? f x x→ = cA (c 为常数). ③ ( ) ( ) lim ? g x f x x→ = lim ( ) lim ( ) ? ? g x f x x x → → B A = ( B 0 ). 注: 应注重法则的前提条件,若前提条件不满足,则法则失效. 如: 错误解法: 0 1 lim sin x x → x 0 0 1 lim limsin 0 x x x → → x = = ; 正确解法: 0 1 lim sin 0 = → x x x . 又如: lim ( ) n x x x →+ + − lim lim n n x x x →+ → + − . 再如: 0 0 0 limcos cos lim lim x x x x x x x → → → = ,是错误的写法,因为 0 lim 0 x B x → = = . 1.3.2 极限的计算方法 1、直接代入法:即 lim ( ) ( ) 0 0 f x f x x x = → . 例 1 4 2 3 1 lim 2 2 1 + − − + →− x x x x x . 解 原式 1 ( 1) 4( 1) 2 ( 1) 3( 1) 1 2 2 = − − + − − − − − + = . 以下各例都无法直接应用法则,需适当的化简后再应用(应清楚每一步求法的根据). 2、 ) 0 0 ( 型:求解的方法是分子和分母同时约去使分母为 0 的式子. 常用的方法有: 因式分解法;提取公因式法;分子或分母有理化法; 1 sin lim 0 = → x x x (下节介绍). 例 2 2 1 lim 2 2 1 + − + →− x x x x x . 解 原式 = − + + = →− (2 1)( 1) ( 1) lim 1 x x x x x 3 1 2 1 lim 1 = →− x − x x . 例 3 x x x x x x + − + → 3 2 2 0 2 3 2 lim . 解 原式 2 2 1 3 2 lim 2 0 = − + − + = → x x x x
例4卿+3-2 x-1 爆原武=册-W232子 x+3-4 1 3、(份型:求解的方法是分子和分母同时除以最大项 2x2-x-1 例5m3x-2x-1 2-11 x22 x x2 2x2-x-1 例6m3x-2x-1 211 解原式=m士子三=0 3-2 xx 2x3-x-1 例7m3-2x-1 11 2- 2¥+33 例8m3-2 解原式=m 1- (3x-2)0 例9m-+2产2x-3
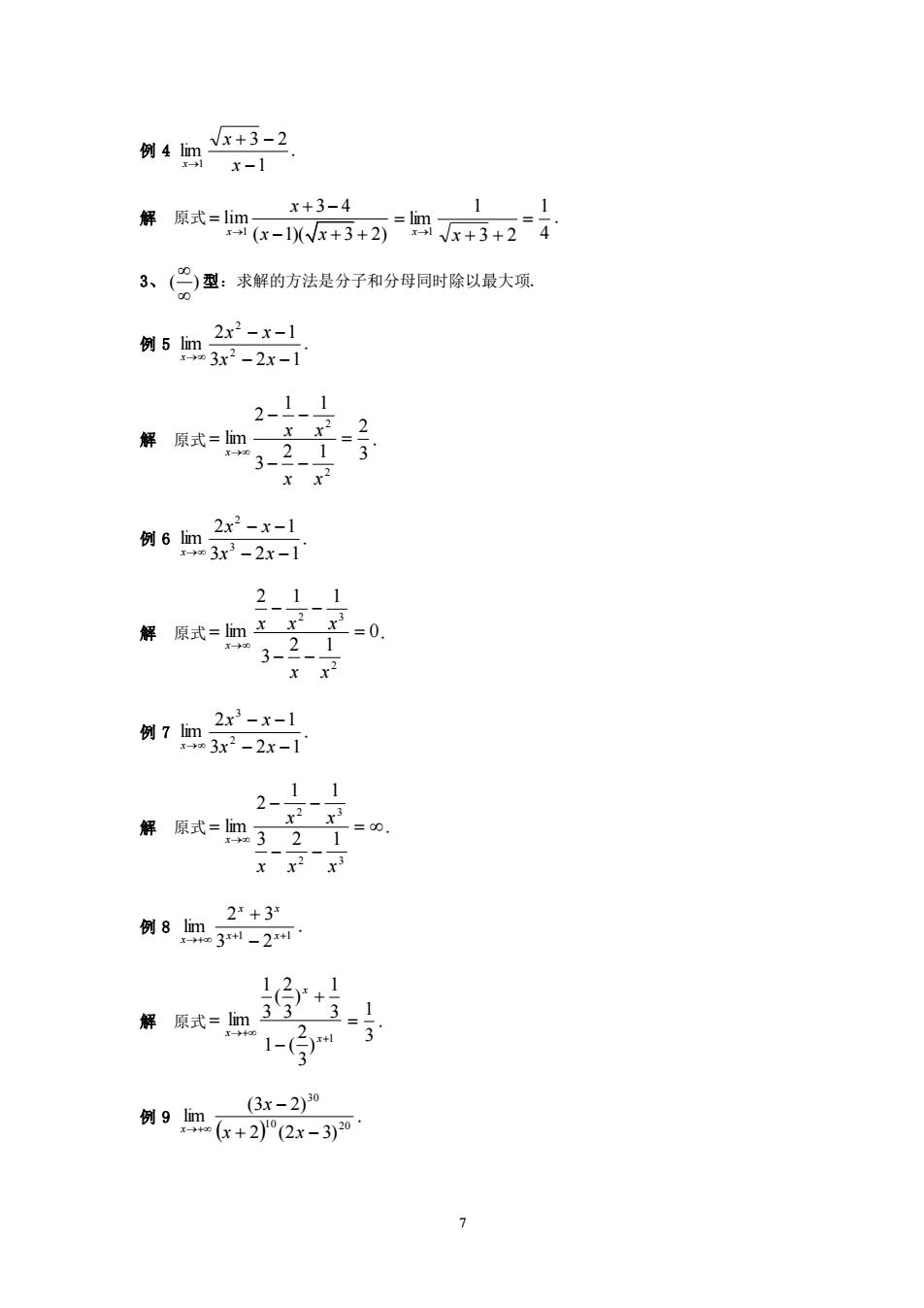
7 例 4 1 3 2 lim 1 − + − → x x x . 解 原式 1 3 4 lim ( 1)( 3 2) x x → x x + − = − + + 4 1 3 2 1 lim 1 = + + = → x x . 3、 ( ) 型:求解的方法是分子和分母同时除以最大项. 例 5 3 2 1 2 1 lim 2 2 − − − − → x x x x x . 解 原式 3 2 2 1 3 1 1 2 lim 2 2 = − − − − = → x x x x x . 例 6 3 2 1 2 1 lim 3 2 − − − − → x x x x x . 解 原式 0 2 1 3 2 1 1 lim 2 2 3 = − − − − = → x x x x x x . 例 7 3 2 1 2 1 lim 2 3 − − − − → x x x x x . 解 原式 = − − − − = → 2 3 2 3 3 2 1 1 1 2 lim x x x x x x . 例 8 1 1 3 2 2 3 lim + + →+ − + x x x x x . 解 原式 1 ) 3 2 1 ( 3 1 ) 3 2 ( 3 1 lim + →+ − + = x x x 3 1 = . 例 9 ( ) 10 20 30 2 (2 3) (3 2) lim + − − →+ x x x x