
奈奎斯特采样定理 ■模拟信号x,()为带限信号; ■最高角频率为2。 ■如采样频率满足( 2.≥22。 ■则理想采样信号x(t)通过增益为T,截止频率为 的低通滤波器G(j2),可唯一地恢复原模拟信号x() ■采样频率的确定: 口防止混叠并降低运算量为原则2。=(3~4)2。 口加预滤波器(抗混叠滤波器) 12
奈奎斯特采样定理 模拟信号 为带限信号; ( ) a x t 最高角频率为 c 如采样频率满足 则理想采样信号 通过增益为 T 截止频率为 2 s c 则理想采样信号 x t ˆ ( ) 通过增益为 T ,截止频率为 的低通滤波器 ,可唯一地恢复原模拟信号 ( ) a x t 2 s G ( ) j ( ) a x t 采样频率的确定: ( ) j 防止混叠并降低运算量为原则 (3 ~ 4) s c 加预滤波器(抗混叠滤波器) 12
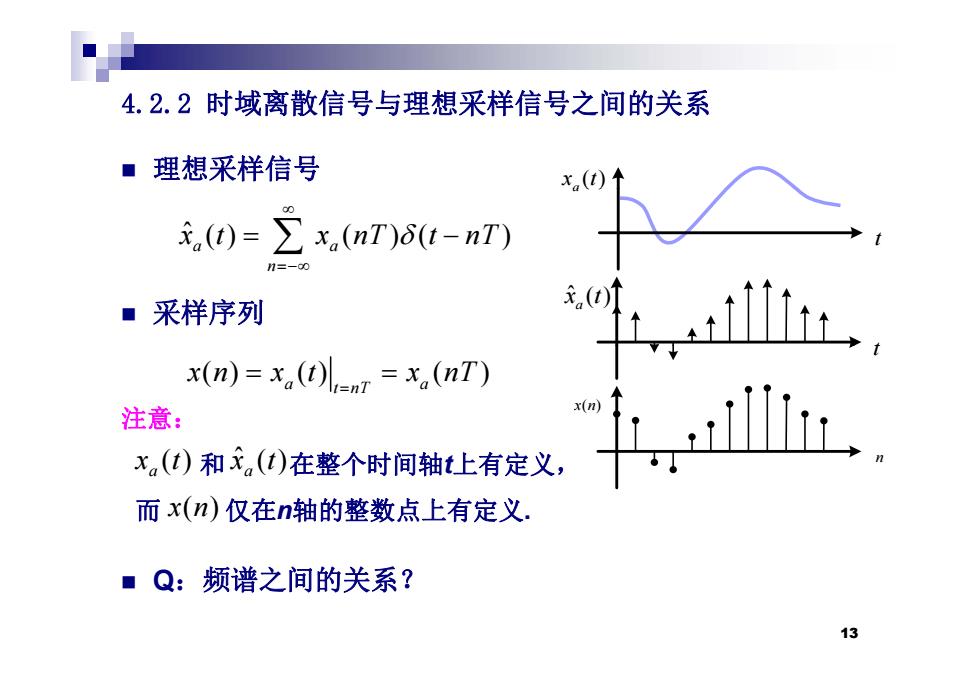
4.2.2时域离散信号与理想采样信号之间的关系 ■理想采样信号 x(t)↑ ,0=∑x,(nT)6t-nT) ■采样序列 (t)T x(n)=x(t)=x(nT) 注意: x(n) x(t)和x(t)在整个时间轴t上有定义, 而x(n)仅在n轴的整数点上有定义. ■Q:频谱之间的关系? 13
4.2.2 时域离散信号与理想采样信号之间的关系 理想采样信号 ( ) a x t ˆ () ( ) ( ) a a n x t x nT t nT ( ) a t 采样序列 n ˆ ( ) a x t t 注意: ( ) () ( ) a a t nT x n x t x nT t x( ) n 注意: 和 在整个时间轴t上有定义, 而 仅在 轴的整数点上有定义 n ( ) a x t ˆ ( ) a x t 而 ( ) 仅在n轴的整数点上有定义. Q:频谱之间的关系? x n( ) Q:频谱之间的关系? 13

()(nT)6(-nT) 理想采样信号的频谱 x(n)=xa(t)=x(nT) (j2)=∫,(t)edt =∫∑x,(nT)6u-nT)edr =2x,nI)jδt-nI)edt =∑x,(nT)eT 14
x t x nT t nT ˆ () ( ) ( ) 理想采样信号的频谱 () ( ) ( ) a a n x t x nT t nT ( ) () ( ) a a t nT x n x t x nT ˆ ( ) () ˆ j t X j x t e dt a a ( )( ) j t x nT t nT e dt ( )( ) a n x nT t nT e dt () ( ) j t a n x nT t nT e dt ( ) j nT a n x nT e n 14

,()=7三X,(0-jm,) ■ 理想采样信号的频谱 (j2)=∑x,(nTeo ■时域离散信号x(n)的频谱 X(e)=∑x(n)eoa ■由于x(n)=xa(nT) 令0=27 X(er)=X(j) X(e)=72X,(n-k,) e)-7三X.号)-7立X.U2 15
1 ˆ () ( ) a as m X j X j jm T 理想采样信号的频谱 ˆ () () j nT a a n X j x nT e 时域离散信号 的频谱 ( ) () j j n n X e x ne x( ) n 由于 令 n () ( ) a x n x nT T ˆ ( ) () j T X a e Xj 1 () ( ) j T a s k X e X j jk T 1 21 2 () ( ) ( ) j a a k X e X j jk X j () ( ) ( ) a a k k jj j T T TT T 15
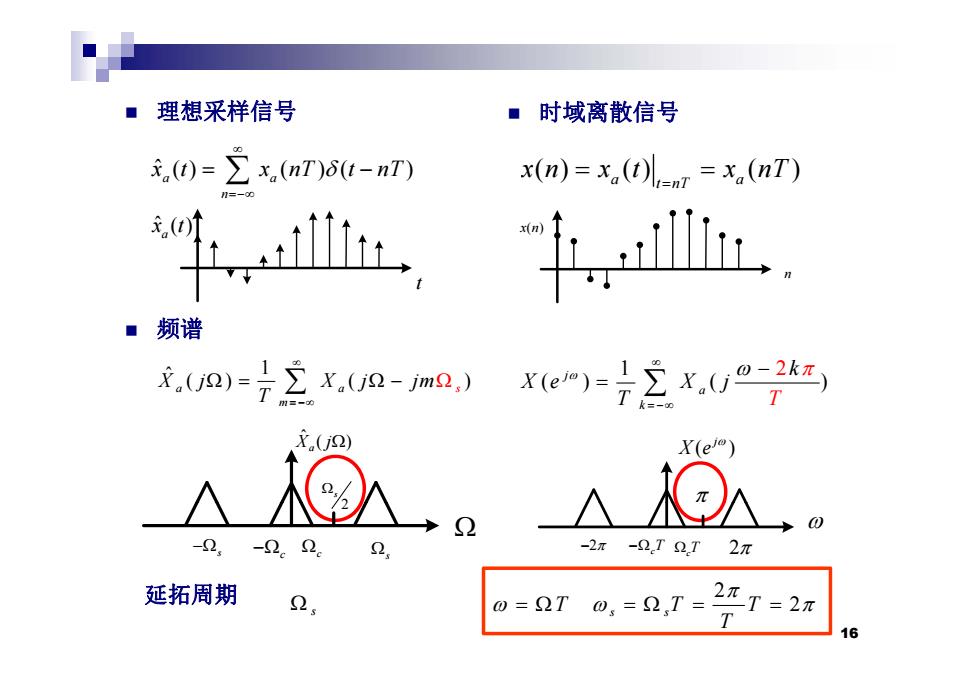
理想采样信号 ■时域离散信号 ,)=∑x,(nI)6t-nI) x(n)=x()l-nr=x,(nT) ■频谱 .)x.-m)x() X.(j2) YX(e) -2.-2.2. -2π-2T2.T2π 延拓周期 0=2T0,=2,T= 2πT=2π T 16
理想采样信号 时域离散信号 ˆ () ( ) ( ) a a x t x nT t nT ( ) () ( ) a a t nT x n x t x nT n ˆ ( ) x( ) n a x t 频谱 n t 1 ˆ () ( ) a a m X j X j jm s T 1 () ( ) j 2 a k k Xe X j T T ( ) j X e ˆ ( ) X j a 2 s 2 cT cT 2 c s s c 2 延拓周期 2 2 T TT s s T s 16