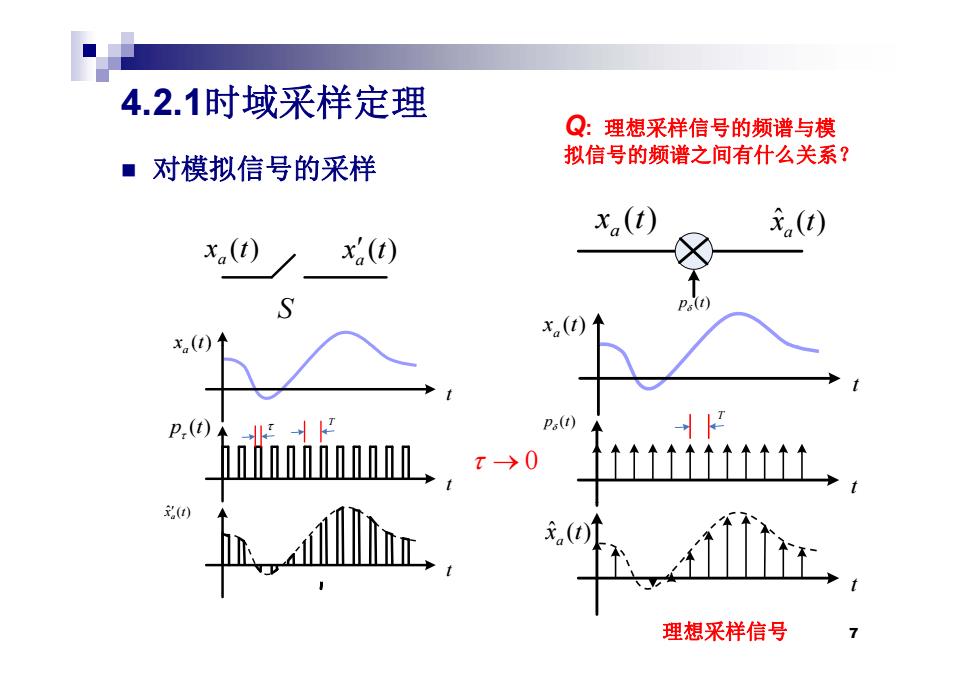
4.2.1时域采样定理 Q:理想采样信号的频谱与模 ■对模拟信号的采样 拟信号的频谱之间有什么关系? x(t) (t) xa (t) x(t) x。(t)1 p.(t) Ps(1) x(t a(t) 理想采样信号
4.2.1时域采样定理 对模拟信号的采样 Q: 理想采样信号的频谱与模 拟信号的频谱之间有什么关系? ( ) a x t ˆ ( ) a x t ( ) a x t ( ) a x t p t( ) ( ) a x t S x t( ) t p t( ) T ( ) a x t p t( ) t T p t( ) t p t( ) t T 0 ˆ ( ) a x t t ˆ ( ) a x t t t 理想采样信号 7

理想采样信号与模拟信号频谱之间的关系 ■单位冲激串 p,()=∑6t-nT) x,(t) (t) ■理想采样信号 ,)=∑x,)6t-nIT)=∑x,nT)8t-nT) ■傅里叶变换 口单位冲激串 P(UQ)=Fp,a=27立oQ-m2) 口采样角频率 Q,= 元=2πF, T
理想采样信号与模拟信号频谱之间的关系 单位冲激串 p () ( ) t t nT 单位冲激串 理想采样信号 () ( ) n p ˆ () () ( ) a a n x t x t t nT ( )( ) a n x nT t nT 傅里叶变换 n n 单位冲激串 2 ( ) [ ( )] ( ) P s j FT p t m 采样角频率 ( ) [ ( )] ( )s m j p T 2 2 F s Fs T 8

傅里叶变换 x (t) 元(t) 口理想采样信号 ) 文,U0)=FI,1=2X,(U0)PU) 2元 X(m2之0-n,川 2π =」x,0)289-m,-0d0 =7立∫X,(/05(0-mn,-0)d0 =立X,(U0-jmn,) 9
傅里叶变换 理想采样信号 1 ˆ ( ) [ () ˆ () () 2 ] 1 2 X j FT x t a a X j Pj a 1 2 [ ( ) ( )] 2 a s m Xj m T 1 () ( ) a s m X j md T 1 ( )( ) X a s j md T T m T m 1 Xj j ( ) a s ( ) m Xj jm T 9
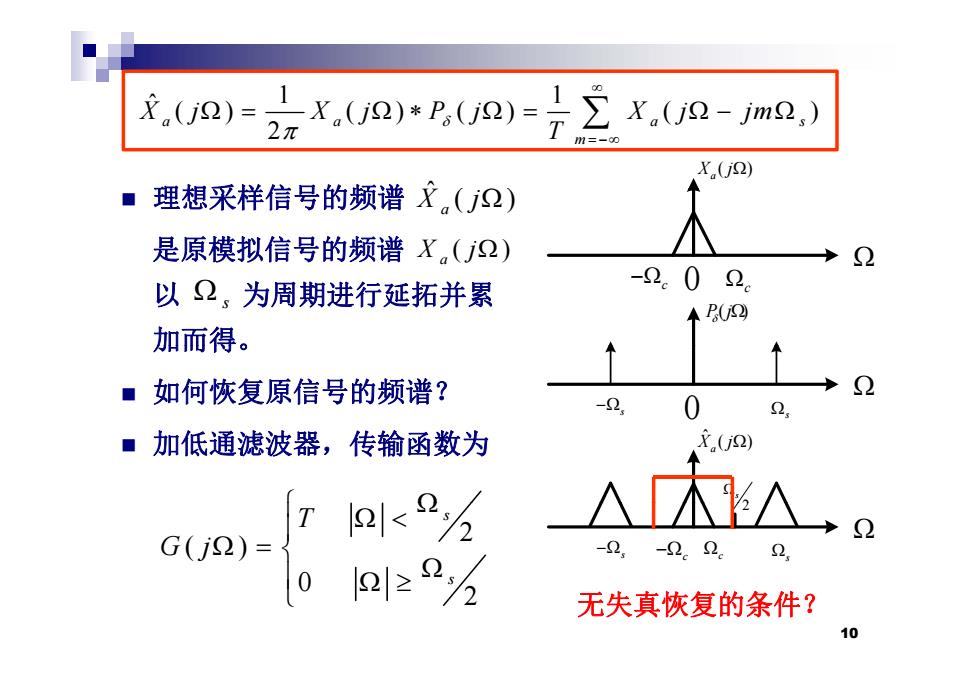
.(x(-m.) X.(j2) ◆ 理想采样信号的频谱.(j2) 是原模拟信号的频谱X,(2) 以2,为周期进行延拓并累 -2.02。 ◆P(2 加而得。 ■如何恢复原信号的频谱? 92 -2 0 2 ■加低通滤波器,传输函数为 X(j2) -2.-2.2. 无失真恢复的条件? 10
1 1 ˆX j X j P j X j jm () () () ( ) 理想采样信号的频谱 ( ) Xa j ˆ ( ) () () () ( ) 2 a a as m X j X j P j X j jm T 理想采样信号的频谱 是原模拟信号的频谱 0 ( ) X a j ( ) X j a 以 为周期进行延拓并累 加而得。 0 c c P j( ) s 加而得。 如何恢复原信号的频谱? 0 s s 加低通滤波器,传输函数为 ˆ ( ) Xa j 2 s c s s c 2 2 ( ) 0 s s T G j 0 2 s 无失真恢复的条件? 10
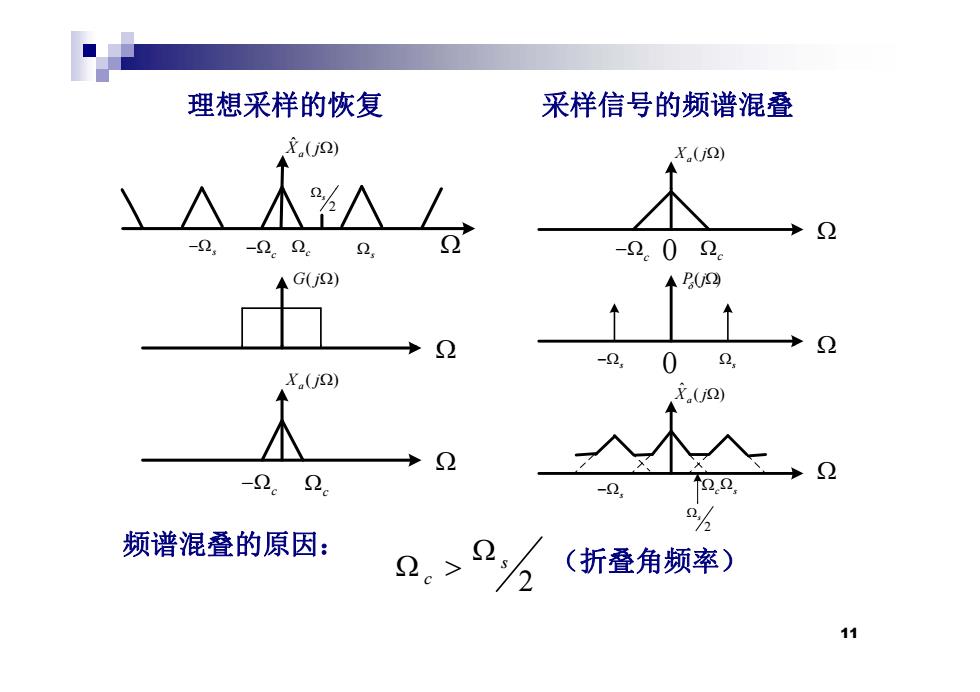
理想采样的恢复 采样信号的频谱混叠 (Uj2) X.(U2) -2-2.2. 2 -2.02e 4G(2) ◆U2 -2 X.(j) X(j -2.2。 T22 2, 频谱混叠的原因: 2。>2/ (折叠角频率) 11
理想采样的恢复 采样信号的频谱混叠 ˆ ( ) Xa j 采样信号的频谱混叠 ( ) Xa j s c c s 2 s c 0 c G j ( ) P j( ) ( ) Xa j s 0 s ˆ ( ) Xa j c c s s c 2 s 频谱混叠的原因: 2 s c (折叠角频率) 2 c 11