
■拉普拉斯方程式的求解有四种方法:1.解析解>数学解析法是根据具体边界条件以解析法求解拉普拉斯方程式。》满足拉普拉斯微分方程的解是两个共轭调和函数即势函数和流函数,该函数描绘出两族相互正交的曲线即等势线和流线。》该法的缺点是当边界条件复杂时定解较难求得。11
11 ◼ 拉普拉斯方程式的求解有四种方法: 1.解析解 ➢ 数学解析法是根据具体边界条件以解析 法求解拉普拉斯方程式。 ➢ 满足拉普拉斯微分方程的解是两个共轭 调和函数即势函数和流函数,该函数描 绘出两族相互正交的曲线即等势线和流 线。 ➢ 该法的缺点是当边界条件复杂时定解较 难求得

2.数值解法>有限差分法和有限单元法。3.实验法实验法是指采用一定比例的模型来摸拟真实的渗流场,用实验手段测定渗流场中的渗流要素。例如电比拟法、电网络法和沙槽模型法等。12
12 2.数值解法 ➢ 有限差分法和有限单元法。 3.实验法 ➢ 实验法是指采用一定比例的模型来摸拟 真实的渗流场,用实验手段测定渗流场 中的渗流要素。例如电比拟法、电网络 法和沙槽模型法等

4.图解法》图解法是指采用绘制流网的方法求解拉普拉斯方程的近似解。》该法具有简便、迅速的优点,并能用于建筑物边界轮廓较复杂的情况。13
13 4.图解法 ➢ 图解法是指采用绘制流网的方法求解拉 普拉斯方程的近似解。 ➢ 该法具有简便、迅速的优点,并能用于 建筑物边界轮廓较复杂的情况

二、流网的绘制及应用■在稳定渗流场中,流线表示水质点的运动路线。等势线是渗流场中势能或测管水头的等值线。由流线和等势线所组成的曲线正交网格称为流网。透水地基上混凝土坝下渗流的流网图见图2-16。14
14 二、流网的绘制及应用 ◼ 在稳定渗流场中,流线表示水质点的运 动路线。等势线是渗流场中势能或测管 水头的等值线。由流线和等势线所组成 的曲线正交网格称为流网。透水地基上 混凝土坝下渗流的流网图见图2-16
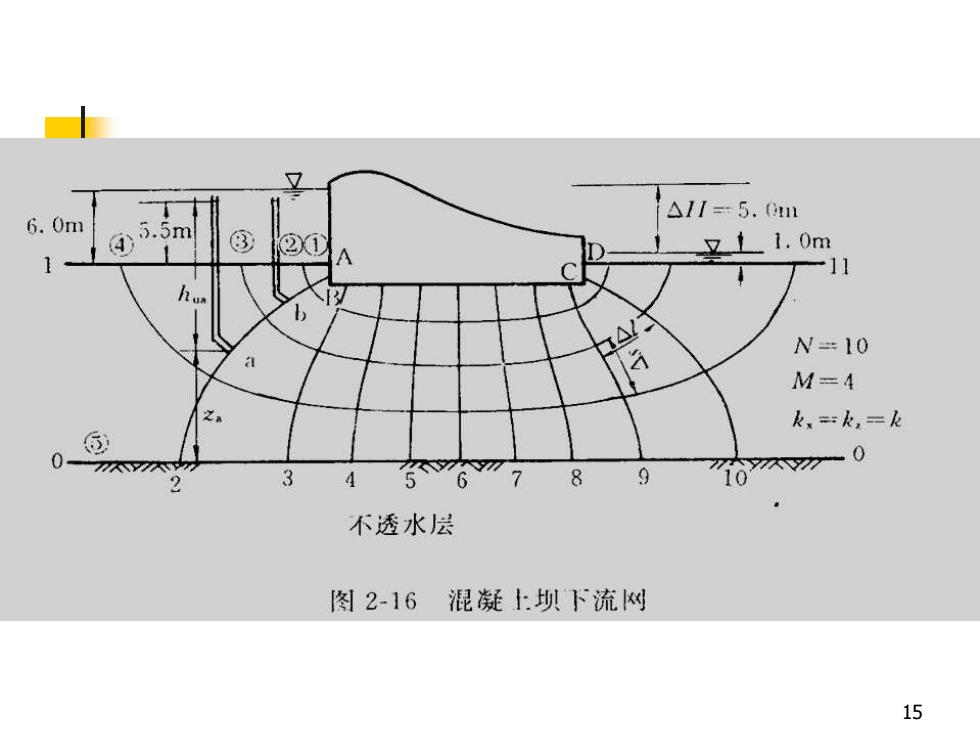
7Al--5.0m6.0m.on81.0m42X111h..N=10M4k==k,k.01958103674.不透水层图2-16混凝上坝下流网15
15