
讨论: 匀速圆周运动 o是恒量 d6=odt一d6=odt一8=8,+o 匀角加速圆周运动 O是恒量 0=o,+0t 02 -o=2ax(0-0。) 一般圆周运动 d0=odt一 =8+∫0od 让美觉返司退
上页 下页 返回 退出 匀角加速圆周运动 是恒量 0 = + t 2 0 0 1 2 = + +t t 0 0 d d t t = 0 0 d t = + t 一般圆周运动 2 2 − = − 0 0 2 ( ) 匀速圆周运动 是恒量 d d = t 0 0 d d t t = = +t 0 讨论:
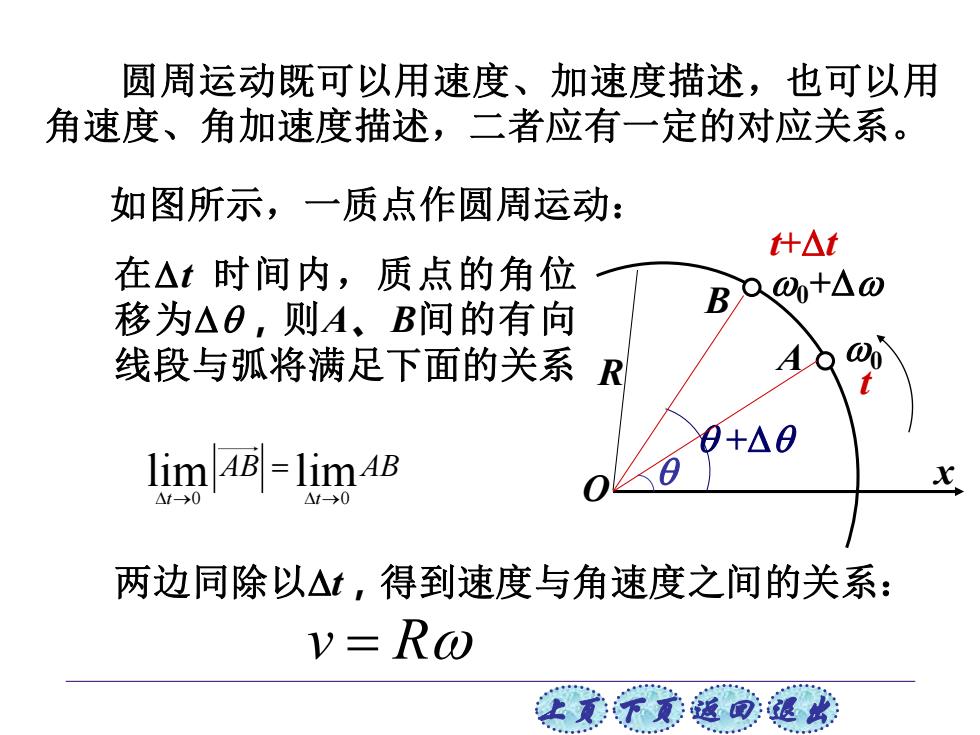
圆周运动既可以用速度、加速度描述,也可以用 角速度、角加速度描述,二者应有一定的对应关系。 如图所示,一质点作圆周运动: 什△t 在△t时间内,质点的角位 B0@+△0 移为△O,则A、B间的有向 线段与弧将满足下面的关系R 8+△0 limB =lim 48 △t-0 两边同除以△,得到速度与角速度之间的关系: v=Ro
上页 下页 返回 退出 R O x 圆周运动既可以用速度、加速度描述,也可以用 角速度、角加速度描述,二者应有一定的对应关系。 + 0 0+ t+t B t A 如图所示,一质点作圆周运动: 在t 时间内,质点的角位 移为,则A、B间的有向 线段与弧将满足下面的关系 两边同除以t,得到速度与角速度之间的关系: v = R 0 0 lim lim t t AB AB → → =

将上式两端对时间求导,得到切向加速度与角 加速度之间的关系:☑=RC 将速度与角速度的关系代入法向加速度的定义 式,得到法向加速度与角速度之间的关系: an Ro R y Ro 线量→速度、加速度 a,Ra 角量→角速度、角加速度 a。= R@2 让意子元道回退此
上页 下页 返回 退出 将上式两端对时间求导,得到切向加速度与角 加速度之间的关系: t a R = 将速度与角速度的关系代入法向加速度的定义 式,得到法向加速度与角速度之间的关系: 2 n v a R = 2 = R 线量 速度、加速度 角量 角速度、角加速度 t 2 n v R a R a R = = =

讨论 1.a,=0,an=0 匀速直线运动 2.4,=c,an=0匀变速直线运动 3.a,=0,a=c 匀速率圆周运动 4.a≠0,an≠0 变速曲线运动 让贰了意通回
上页 下页 返回 退出 t n 1. 0 , 0 a a = = 匀速直线运动 匀变速直线运动 匀速率圆周运动 变速曲线运动 t n 2 . , 0 a c a = = t n 3. 0 , a a c = = t n 4 . 0 , 0 a a 讨论: