
狄里赫利条件:若周期函数,a、在每个周期中连 续,或只有有限个第一类间断点;b、在每个周期 中只有有限个极值(包括极大和极小),则傅立叶 级数收敛。 f(x) 连续点 级数之和 fx+0)+fs-0 在间断点. 11
1111 狄里赫利条件:若周期函数,a、在每个周期中连 续,或只有有限个第一类间断点;b、在每个周期 中只有有限个极值(包括极大和极小),则傅立叶 级数收敛。 级数之和 ( ) ( 0 0 ) ( ) 2 f x f x f x = + + − 连续点 在间断点
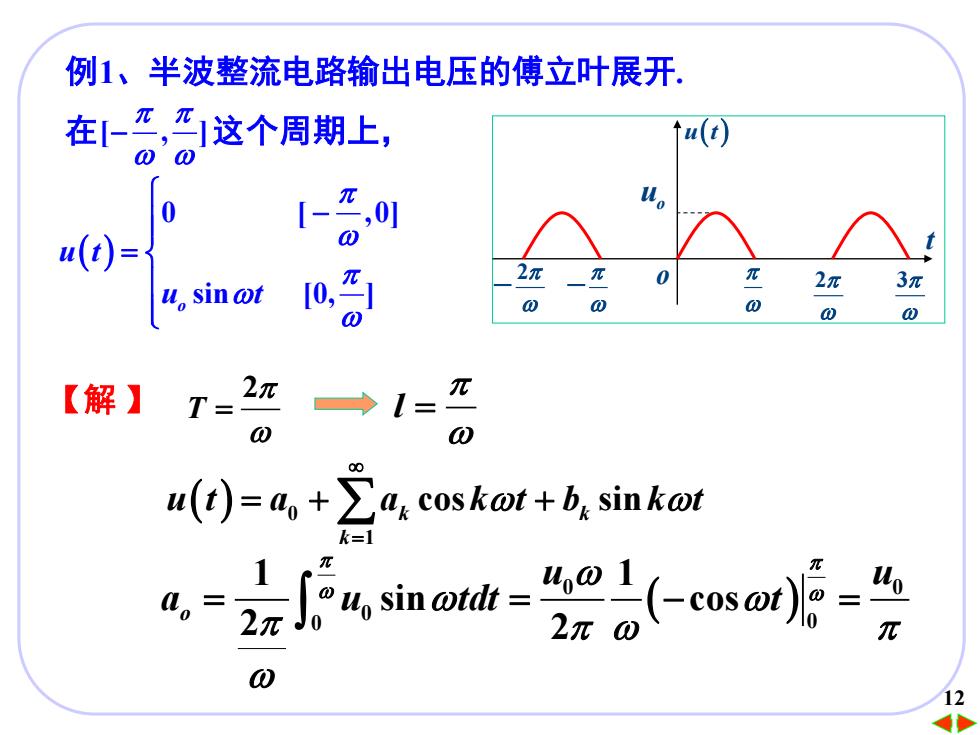
例1、半波整流电路输出电压的傅立叶展开, 在-π,这个周期上, π u(i 0 u()= 2π 10, 2 3π u,sin @t 0 0 0 0 【解】 T=20 2π →l= 0 a(t)=a+>a,coskat+b sinkor k=1 anow-=2h-csom8 1 0,= 2π 元 0 12
1212 例1、半波整流电路输出电压的傅立叶展开. 在 这个周期上, 2 - - 2 3 u t( ) t uo o [ , ] − ( ) 0 [ ,0] sin [0, ] o u t u t − = 【解 】 2 T = ( ) 0 1 k k cos sin k u t a a k t b k t = = + + ( ) 0 0 0 0 0 1 1 sin cos 2 2 o u u a u tdt t = = − = l =

1 = 元 u sin ot cos kotdt 0 sin(+k)ol+-sin(1-k)or P-cos(1+k)@t-cos(1-k)@t 2π (1+k)o(1-k) an (k=奇) (k=偶) 13
1313 0 1 sin cos k o a u t k tdt = ( ) ( ) 0 sin 1 sin 1 2 uo k t k t dt = + + − ( ) ( ) ( ) ( ) 1 0 cos 1 cos 1 2 1 1 k o u k t k t k k − + − − = + + − ( ) ( ) ( ) ( ) ( ) 1 2 2 0 1 1 2 1 1 k o o k u u k k k + = − − = − − =奇 =偶

1 41= u,sinot cosotdt=0,(k=1) 元J0 ⊙ 1 u,sin ot sin kotdt π 0 2元 Lc(1-k)at-co(1+)aiy 2π 岁f 1 b1= u,sin'otdt 元J0 2 ⊙ 14
1414 ( ) 1 0 1 sin cos 0, 1 o a u t tdt k = = = 0 1 b u t k tdt k o sin sin = ( ) ( ) 0 cos 1 cos 1 2 uo k t k t dt = − − + ( ) ( ) ( ) ( ) 1 0 sin 1 sin 1 0 2 1 1 k o u k t k t k k − + = − = − + 2 1 0 1 sin 2 o o u b u tdt = =

u(t)= +sin+2%. 1 π1-4k2 os2kot π 2 。+ uo sin @t- os2@t π 2 3π 2,c0s4t- 15元 2Lnc0s6ot+. 35π 【讨论】 常数项 :直流成份,为次级电压峰值的二≈0.32; 元 sinwt:基波,圆频率为o, 2 振幅为 2 2u cos2ot:二次谐波,振幅 2。≈0.21 3元 3π 2u cos4ot:四次谐波,振幅为 15元 2。≈0.04 15π 15
1515 ( ) 2 1 2 1 sin cos 2 2 1 4 o o o k u u u u t t k t k = = + + − 2 2 2 sin cos 2 cos4 cos6 . 2 3 15 35 u u u u u o o o o o t t t t = + − − − + 【讨论 】 常数项 o : u 直流成份,为次级电压峰值的 1 0.32; sin : 2 uo t 基波,圆频率为,振幅为 ; 2 uo 2 cos 2 : 3 uo t − 二次谐波,振幅为 2 0.21 ; 3 o o u u 2 cos4 : 15 uo t − 四次谐波,振幅为 2 0.04 ; 15 o o u u