
2u cos6ot:六次谐波,振幅为 35 2。≈0.02, 35π 振 Mo 0.5uo 0.32u。 0.21u 0.04w 频率 2030 405060 半波整流后,除了直流成份外仍然有交流成份,其中基波 成份还是比较大,越是高次的偶次谐波的振幅越小,在 实际应用中可略去不计。 16 D
1616 2 cos6 : 35 uo t − 六次谐波,振幅为 2 0.02 . 35 o o u u 0.5uo 0.32uo 0.21uo 0.04uo uo o 2 3 4 5 6 频率 振 幅 半波整流后,除了直流成份外仍然有交流成份,其中基波 成份还是比较大,越是高次的偶次谐波的振幅越小,在 实际应用中可略去不计
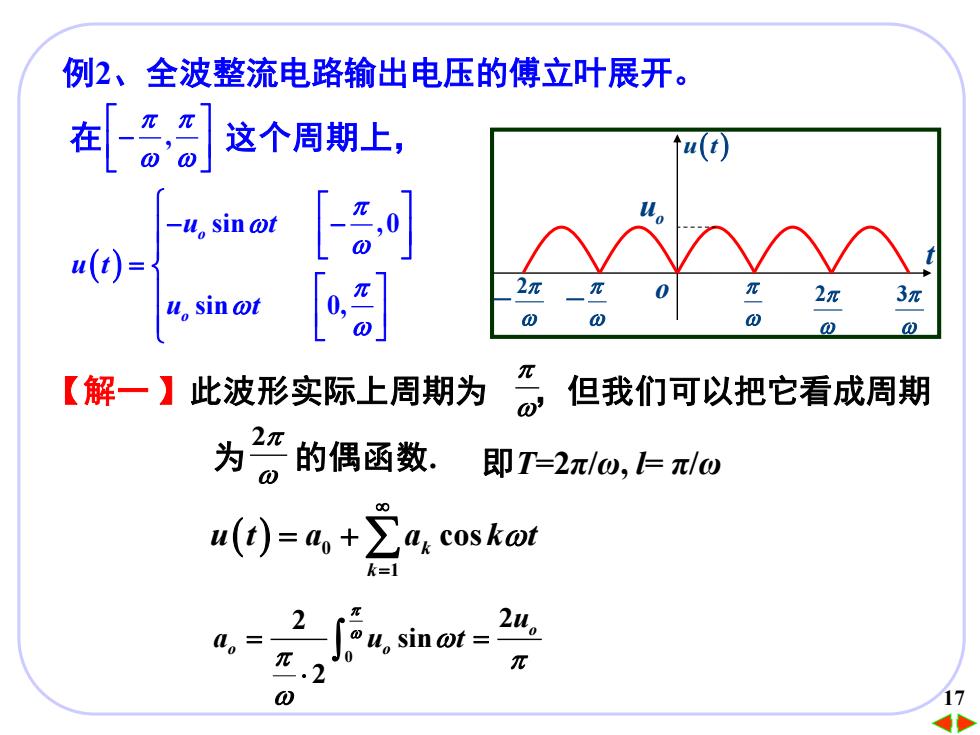
例2、全波整流电路输出电压的傅立叶展开。 在日 这个周期上, u(t) -u,sin @t u())= 2 2元 0 u,sin ot 2π 3π 0 0 【解一】此波形实际上周期为 但我们可以把它看成周期 为2 的偶函数. 即T=2π/0,l=π/w ∫,sin of= π .2 0 17
1717 例2、全波整流电路输出电压的傅立叶展开。 在 , 这个周期上, − ( ) sin ,0 sin 0, o o u t u t u t − − = 2 - - 2 3 u t( ) t uo o 【解一 】此波形实际上周期为 ,但我们可以把它看成周期 为 的偶函数. 2 ( ) 0 1 cos k k u t a a k t = = + 0 2 2 sin 2 o o o u a u t = = 即T=2π/ω, l= π/ω

2 0k= u,sin ot cos kotdt πJ0 0 ="2f[nu+约a+sml-)adw e-cs(1+K)oL.-cos(1-K)ot7 (1+)oT (1-k)w o 品-( (k=奇) (k=偶) 18 4D
1818 0 2 sin cos k o a u t k tdt = ( ) ( ) 0 sin 1 sin 1 uo k t k t dt = + + − ( ) ( ) ( ) ( ) 1 0 cos 1 cos 1 1 1 k o u k t k t k k − + − − = + + − ( ) ( ) ( ) ( ) ( ) 1 2 2 0 2 1 1 4 1 1 k o o k u u k k k + = − − = − − =奇 =偶

2 01= 元J0 u,sinotcosotdt=0,(k=1) 0 u(t) 2+ 41 00 元1-4k2cos2kor 4.c0s20t- π3 4ucos4@t- 15π 4。cos6t+. 35π 【解二】把a0看成周期为=元 的函数,则: u(t)=a+∑xcos2kot k=1 1 2uo 0。= u,sin @t= π 0 .2 20 19
1919 ( ) 1 0 2 sin cos 0, 1 o a u t tdt k = = = ( ) 2 1 2 4 1 cos 2 1 4 o o k u u u t k t k = = + − 2 4 4 4 cos 2 cos4 cos6 3 15 35 u u u u o o o o t t t = − − − + 【解二 】把u(t)看成周期为 的函数,则: 2 l = ( ) 0 1 cos 2 k k u t a a k t = = + 0 1 2 sin 2 2 o o o u a u t = =

1 元J0 u sin ot cos2kotdt 20 -2[sn(1+2)a+m1-20)oh0 (t)= +,1 名1-4k2cos2kor 【讨论】 常数项 2”:直流成份,为次级电压峰值的 2 -≈0.64; π π Au 2cos2ot:二次谐波,振幅 3 4u。≈0.42u5 3π A acos4ot:四次谐波,振幅为 15 4。≈0.08u 15π 20 4D
2020 0 1 sin cos 2 2 k o a u t k tdt = ( ) ( ) 0 sin 1 2 sin 1 2 uo k t k t dt = + + − ( ) 2 4 1 4 uo k = − ( ) 2 1 2 4 1 cos 2 1 4 o o k u u u t k t k = = + − 【讨论 】 常数项 2 : uo 直流成份,为次级电压峰值的 2 0.64; 4 cos 2 : 3 uo t − 二次谐波,振幅为 4 0.42 ; 3 o o u u 4 cos4 : 15 uo t − 四次谐波,振幅为 4 0.08 ; 15 o o u u