福州大学：《数学物理方法》课程教学资源（PPT课件）第十一章 球函数

第十一章球函数 511.1球坐标系下的拉氏方程的解 1 3 1 Ou =0 r2sine00 r2sin2 0 002 令：u(r,0,p)=R(r)⑧(0)Φ(p） 其中0<p≤2π，0<0≤π. rΦd d R8dPΦ 2 rsin20 d0 sin de r2sin20 d'p 0 同乘以 [2 dr d 1 Φ” R⊙Φ =0 R dr dr) ⊙sinθde sin20Φ 1 d 2 dR R dr dr ⊙sin d0 de sin20Φ 元R=0:

1 第十一章 球函数 §11.1 球坐标系下的拉氏方程的解 2 2 2 2 2 2 2 1 1 1 sin 0 sin sin u u u r r r r r r                    + + =          其中 0 2 , 0 .         令：u r R r ( , ,    ) =   ( ) ( ) ( ) 2 2 2 2 2 2 2 2 sin 0, sin sin d dR R d d R d r r r r d dr dr d d                    + + =     2 : r R 同乘以 " 2 2 1 1 1 sin 0 sin sin d dR d d r R dr dr d d                + + =       " 2 2 1 1 1 sin sin sin d dR d d r R dr dr d d                = − −       =  2 0; d dR r R dr dr      − =  

1 d do 1 sin0 +九=0. ⊙sin0 do de sin20Φ sine d do Asin20=- Φ1 sinθ Φ =, ⑧ de de sino d( de ined +(asn8-9=0, Φ+Φ=0. u(r,8,p+2r)=(r,0,p),→p(p+2x)=Φ(p) Φ"+Φ=0 该本征值问题在圆形区域 Φ(p+2x)=Φ(p） 中的拉氏方程中见过 =m,u=m2 (m=0,1,2,.)9 Φ=C1c0smp+c2 sinmp, 或重~eimp m=0,±1，±2，.） 2

2 " 2 1 1 sin 0. sin sin d d d d             + + =     " 2 sin sin sin d d d d             + = −     = , ( ) 2 sin sin sin 0, d d d d             + −  =   "  +  =  0. u r u r ( , , 2 , , ,      + =) ( )  + =  (   2 ) ( ) ( ) ( ) " 0 2      +  =   + =  该本征值问题在圆形区域 中的拉氏方程中见过. ( ) 2   = = =    m m m , 0,1,2, , 1 2  = + c m c m cos sin ,   ~ 0, 1, 2, ( ) im e m  或  =   

do sin sin de de +(2sim20-m2)o=0, 1 d =0, sine de 令：x=cs0,⊙(0)→y(x) dd dxddcos0 de dx de dx do -=-sino d =0 y=0, -a-m y=0 3

3 ( ) 2 2 sin sin sin 0, d d m d d            + −  =   2 2 1 sin 0, sin sin d d m d d              + −  =       令：x y x =  → cos ,  ( ) ( ) cos sin d d dx d d d d dx d dx d dx      =  = = − ( ) ( ) 2 2 1 sin sin sin 0, sin sin d dy m y dx dx           − − + − =         2 2 2 sin 0, sin d dy m y dx dx          + − =       ( ) 2 2 2 1 0, 1 d dy m x y dx dx x        − + − =       −

在x=±1（日=0，）处存在自然型边条件y以=±1=有界， ylt=有界 可以证明只有在入=1(1+1) (1=0,1,2,)时，缔合勒让德 方程在x=±1处才有有限解. -a][+]= 1阶缔合勒让德方程 该本征值问题的本征函数是！阶缔合勒让德函数 y(x)~P"(x),即⑧()~P"(cs) 径向方程为： -1(1+)R=0, RdR+2r dR dr2 -1(1+1)R=0.人 欧勒齐次型方程

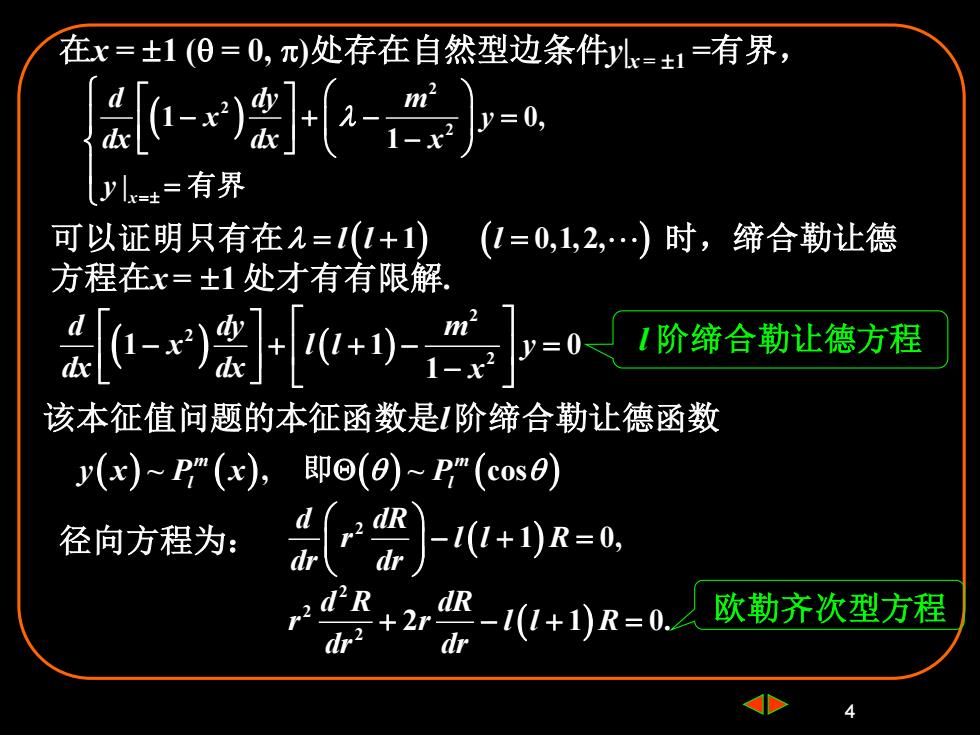
4 在x = 1 ( = 0, )处存在自然型边条件y|x = 1 =有界， ( ) 2 2 2 1 0, 1 | x d dy m x y dx dx x y  =          − + − =        −  =  有界 可以证明只有在 时，缔合勒让德 方程在x = 1 处才有有限解.  = + =  l l l ( 1 0,1,2, ) ( ) ( ) ( ) 2 2 2 1 1 0 1 d dy m x l l y dx dx x       − + + − =       − l 阶缔合勒让德方程 该本征值问题的本征函数是l 阶缔合勒让德函数 ( ) ~ , ~ cos ( ) ( ) ( ) m m l l y x P x P 即   径向方程为： ( ) 2 1 0, d dR r l l R dr dr     − + =   ( ) 2 2 2 2 1 0. d R dR r r l l R dr dr + − + = 欧勒齐次型方程

设R()~r”,代入方程此较项的系数： n(n-1)+2n-l(l+1)=0 →(n-0(n+l+1)=0 =1,%,=-(1+), R(r)=c →u(r,0,p)=R(r)o(0)Φ(p) oip)(cos)CD =0m= 当m>l时，P"(cos)≡0， u(r.0)sinmp (cos0)CD 若问题为轴对称（与φ无关）则m=0, ko-含+BR(m-2+8,)P(w) 对球内对称问题，排除：(，)=∑4rP(cos)

5 ( ) ~ n 设 R r r ，代入方程比较r n项的系数： n n n l l ( − + − + = 1 2 1 0 ) ( ) (n l n l − + + = )( 1 0 ) ( ) 1 2 n l n l = = − + , 1 , ( ) 3 4 1 1 . l R r c r c l r + = + u r R r ( , ,     ) =   ( ) ( ) ( ) ( ) ( ) , , , , 1 0 0 1 cos sin cos m l l m l m l l m l m l l m A m B m P C r D r      + = =   = + +       m l  (cos 0, ) m 当 时， Pl   ( ) ( ) ( ) , , , , 1 0 0 1 , , cos sin cos l m l l m l m l l m l m l l m u r A m B m P C r D r       + = =   = + +       若问题为轴对称（与无关）则m = 0, ( ) ( ) ( ) 0 1 1 0 0 1 1 , cos cos l l l l l l l l l l l l u r A r B P A r B P r r      + + = =     = + = +           对球内对称问题，排除 1 1 : l r + ( ) ( ) 0 , cos l l l l u r A r P    = = 