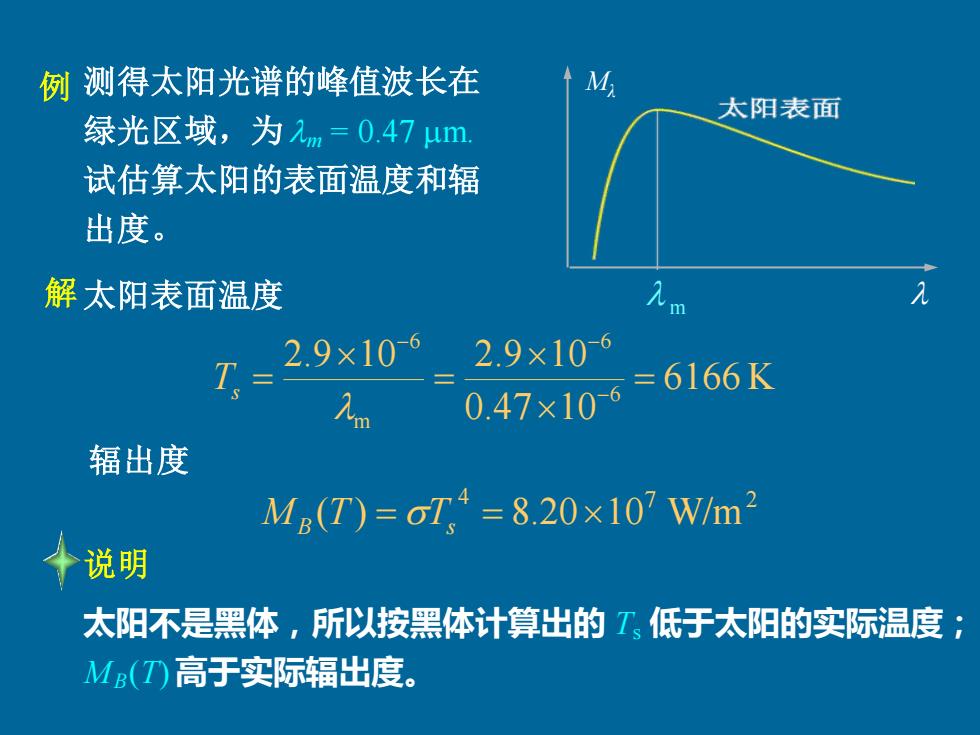
例测得太阳光谱的峰值波长在 M 太阳表面 绿光区域,为m=0.47um 试估算太阳的表面温度和辐 出度。 解太阳表面温度 入四 入 2.9×106 2.9×106 0.47×106 =6166K 辐出度 M.(T)=oT4=8.20×10Wm2 ◆说明 太阳不是黑体,所以按黑体计算出的T低于太阳的实际温度; MB(T)高于实际辐出度
太阳表面温度 Mλ m 6166 K 0.47 10 2.9 10 2.9 10 6 6 m 6 = = = − − − Ts 4 7 2 MB (T) = Ts = 8.2010 W/m 辐出度 测得太阳光谱的峰值波长在 绿光区域,为m = 0.47 m. 试估算太阳的表面温度和辐 出度。 例 太阳不是黑体,所以按黑体计算出的 Ts 低于太阳的实际温度; MB(T)高于实际辐出度。 说明 解
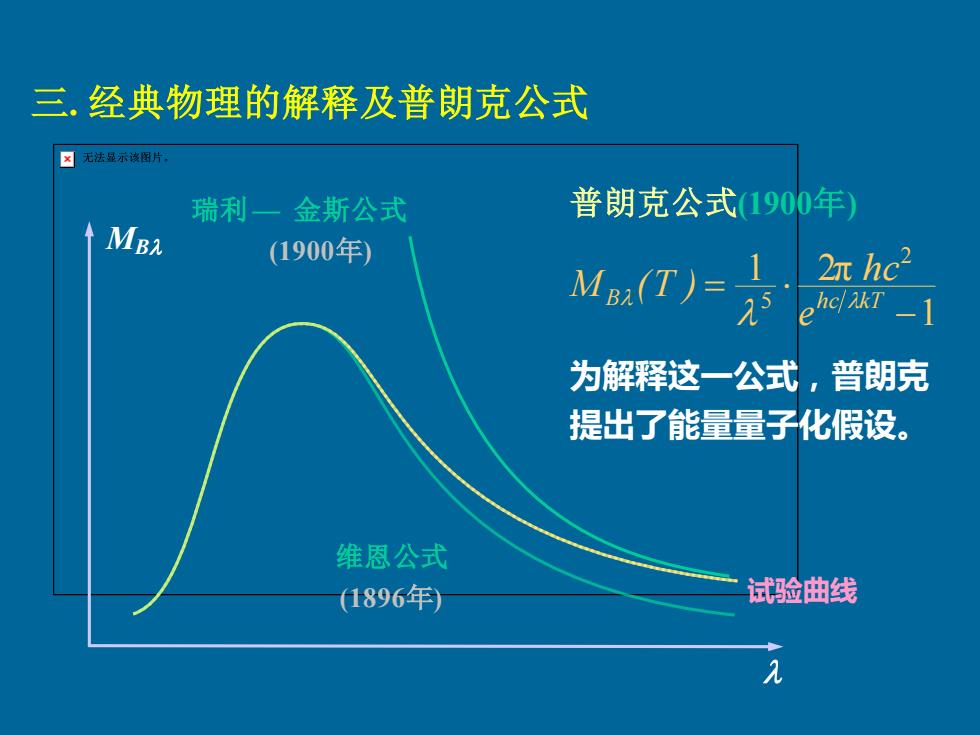
三,经典物理的解释及普朗克公式 ☒无法显示该图片 瑞利一金斯公式 普朗克公式1900年 MB元 (1900年) M(T)=1: 2n hc2 为解释这一公式,普朗克 提出了能量量子化假设。 维恩公式 (1896年 试验曲线 入
三. 经典物理的解释及普朗克公式 MB 瑞利 — 金斯公式 (1900年) 维恩公式 (1896年) 1 1 2π 2 5 − = B hc kT e hc M (T ) 普朗克公式(1900年) 为解释这一公式,普朗克 提出了能量量子化假设。 试验曲线
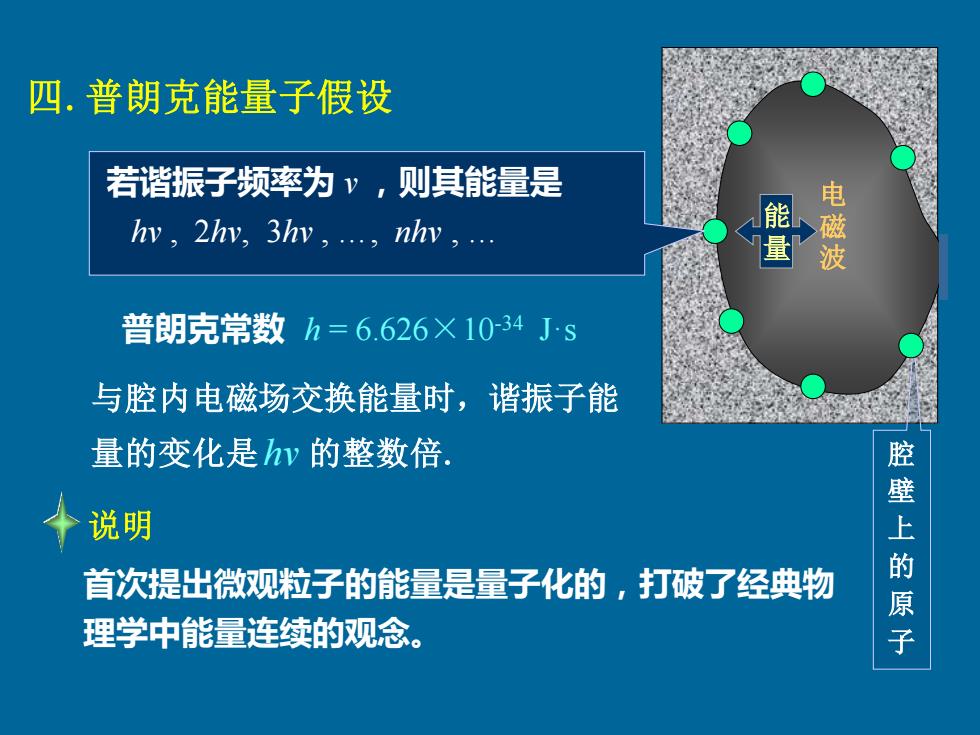
四.普朗克能量子假设 若谐振子频率为ⅴ,则其能量是 hy,2hy,3hv,.,nhv,. 电磁 量 普朗克常数h=6.626×10-34Js 与腔内电磁场交换能量时,谐振子能 量的变化是v的整数倍 说明 首次提出微观粒子的能量是量子化的,打破了经典物 腔壁上的原 理学中能量连续的观念
电 磁 波 四.普朗克能量子假设 若谐振子频率为 v ,则其能量是 hv , 2hv, 3hv , ., nhv , . 首次提出微观粒子的能量是量子化的,打破了经典物 理学中能量连续的观念。 普朗克常数 h = 6.626×10-34 J·s 腔 壁 上 的 原 子 能 量 与腔内电磁场交换能量时,谐振子能 量的变化是hv 的整数倍. 说明
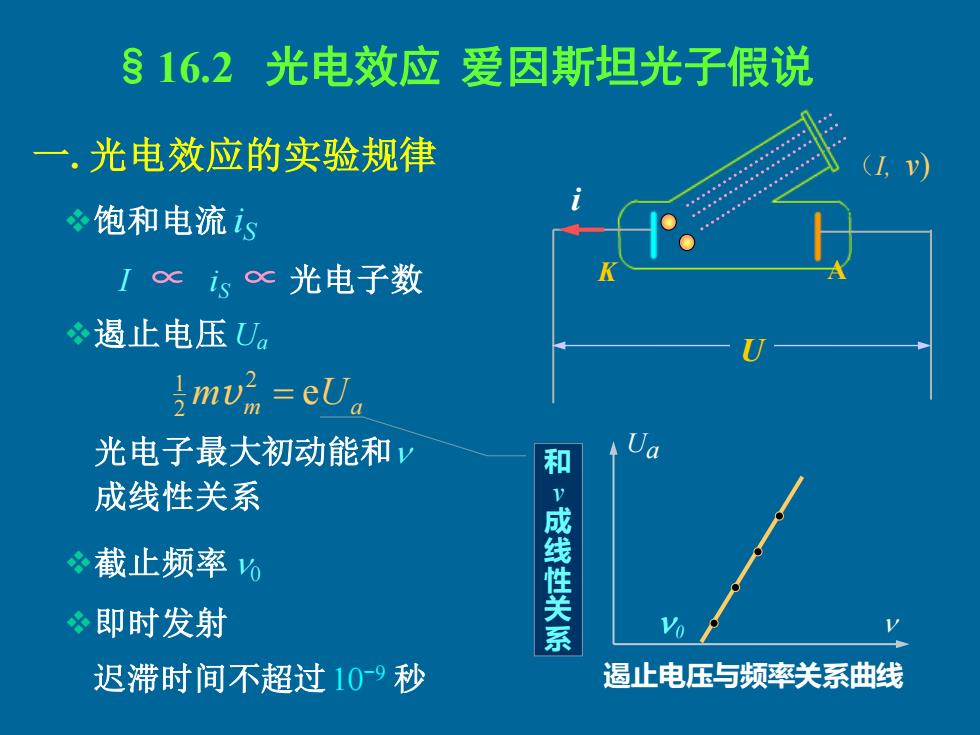
§16.2光电效应爱因斯坦光子假说 一,光电效应的实验规律 饱和电流is Icis心光电子数 冬遏止电压Ua mwm=eU。 光电子最大初动能和 和 Ua 成线性关系 截止频率% 即时发射 "成线性关系 Vo 迟滞时间不超过109秒 遏止电压与频率关系曲线
伏安特性曲线 一. 光电效应的实验规律 ❖饱和电流 iS ❖遏止电压 Ua iS ∝ 光电子数 m m Ua e 2 2 1 v = I ∝ (I, v) K A U §16.2 光电效应 爱因斯坦光子假说 iS3 iS1 iS2 I1 I2 I3 Ua U i I1>I2>I3 Ua 0 光电子最大初动能和 成线性关系 ❖截止频率0 ❖即时发射 迟滞时间不超过10-9 秒 遏止电压与频率关系曲线 和 v 成 线 性 关 系 i

总结 只有光的频率y≥%时,电子才会逸出。 ·光电子最大初动能和光频率y成线性关系。 ·逸出光电子的多少取决于光强I。 ·光电子即时发射,滞后时间不超过109秒。 二,经典物理与实验规律的矛盾 ·电子在电磁波作用下作受迫振动,直到获得足够能量(与 光强1有关)逸出,不应存在红限%。 ·光电子最大初动能取决于光强,和光的频率y无关。 ·当光强很小时,电子要逸出,必须经较长时间的能量积累
二. 经典物理与实验规律的矛盾 • 电子在电磁波作用下作受迫振动,直到获得足够能量(与 光强 I 有关) 逸出,不应存在红限0 。 • 当光强很小时,电子要逸出,必须经较长时间的能量积累。 • 只有光的频率 0 时,电子才会逸出。 • 逸出光电子的多少取决于光强I 。 • 光电子即时发射,滞后时间不超过10–9 秒。 总结 • 光电子最大初动能和光频率成线性关系。 • 光电子最大初动能取决于光强,和光的频率 无关