
式(2.2-1)中,由a,cos ne0,t+b sin no,t=C cos(n@,f-9) 可得f(t)的另一种表达式 f0-号+c,ow0may-0) (2.2-5) 其中 c,=V0+6好:%,=arctan Co ao an 《通后原理课件》
《通信原理课件》

2、指数形式的傅里叶级数 利用欧拉公式C0Sx= 可得的指数表达式 2 f0)=∑F.cmew (2.2-6) n=-c0 式中 E=77f0ehn=0士山,2±3 Fo=Co=do F= (称为复振幅): (是F,的共轭)。 2 《通信原理课件》
《通信原理课件》 2、指数形式的傅里叶级数 利用欧拉公式 可得的指数表达式 式中 cos 2 jx jx e e x − + = 0 ( ) jn t n n f t F e =− = (2.2-6) 0 / 2 / 2 1 ( ) T jn t n T F f t e dt T − − = n = 0, 1, 2. 3, , F c a 0 0 0 = = 2 n n j n c F e− = (称为复振幅); * 2 n n j n n c F e F − = = (是 F n 的共轭)

2、指数形式的傅里叶级数 利用欧拉公式CoSx= 可得的指数表达式 2 00 f0=∑F,emw (2.2-6) 式中 R=7 n=0,h,2±3 1o=co=do F= (称为复振幅): 2 (是F,的共轭)。 2 《通信原理课件》
《通信原理课件》

2.2.2非周期信号的傅里叶变换 前面介绍了用傅里叶级数表示一个周期信号的方法, 对非周期信号,不能用傅里叶级数直接表示,但非周期信 号可看作是T→0的周期信号。这样周期信号的频谱分 析可以推广到非周期信号。 让我们考虑如图2-1(a)所示非周期信号f(t),由其 构造一个周期信号f(t),其周期为T,如图2-1(b)所 示。不难看出,当T→o时,则在-0<t<+0区 间T→o,即m()=。因此,我们可以研究 当f(t)=f(t),周期信号f(t)的傅里叶级数的变化情况。 《通后原理课件》
《通信原理课件》
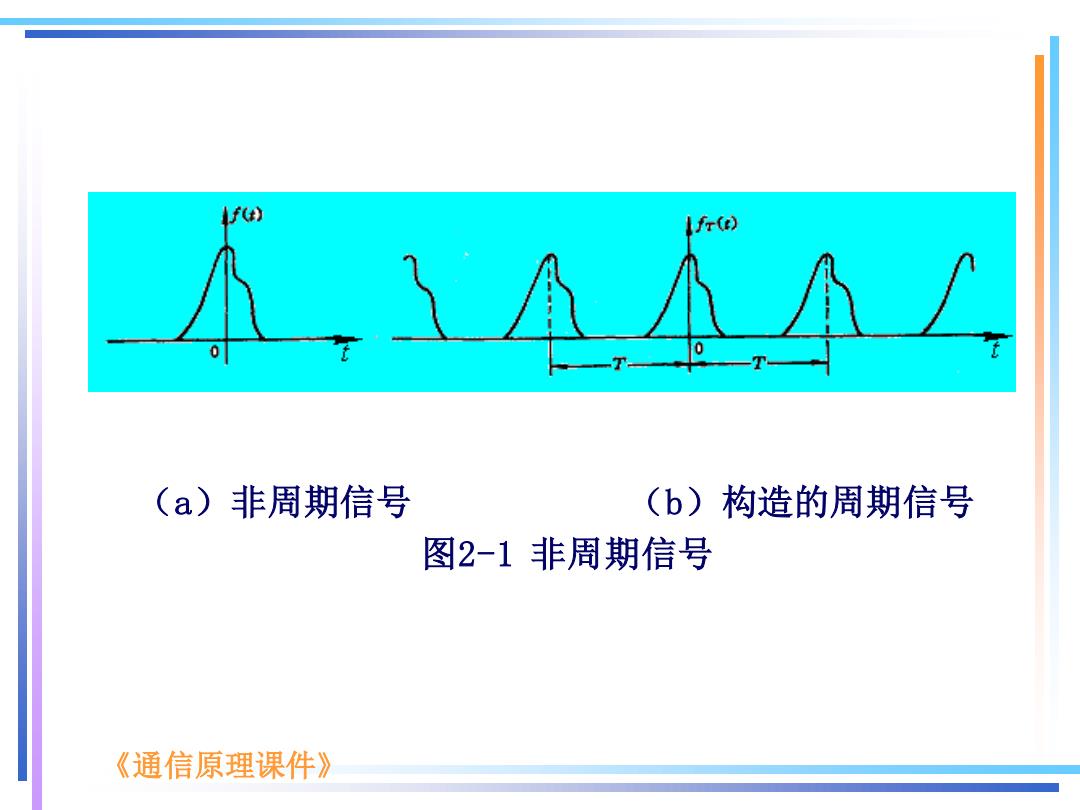
lfu) Ifr() (a)非周期信号 (b)构造的周期信号 图2-1非周期信号 《通信原理课件》
《通信原理课件》 (a)非周期信号 (b)构造的周期信号 图2-1 非周期信号