
二.晶向、晶面和它们的标志: 晶体的一个基本特点是各向异性,沿晶格的不同 方向晶体的性质不同,因此有必要识别和标志晶格中 的不同方向。 点阵的格点可以分列在一 系列平行的直线系上,这些直 线系称作晶列。同一点阵可以 形成不同的晶列,每一个晶列 定义一个方向,称作晶向。如 果从一个阵点到最近一个阵点 的位移矢量为:(以基矢为单 位)1a1+1☑2a2+1,a3 图1-16晶列 则晶向就用[14]来标志
二. 晶向、晶面和它们的标志: 晶体的一个基本特点是各向异性,沿晶格的不同 方向晶体的性质不同,因此有必要识别和标志晶格中 的不同方向。 点阵的格点可以分列在一 系列平行的直线系上,这些直 线系称作晶列。同一点阵可以 形成不同的晶列,每一个晶列 定义一个方向,称作晶向。如 果从一个阵点到最近一个阵点 的位移矢量为:(以基矢为单 位) 则晶向就用 来标志。 11 2 2 33 la la la + + [lll 123 ]

按照上述方法确定的简立方晶格的晶向如图所示, 晶向指数和坐标系的 选取有关,OA的反方 [001叫 向记做100,由于 立方晶格的对称性, 沿立方边的6个晶向 cf [10o],[i00]-,[010],[oi0],[0o1],[0oi] 是等价的,记做: <100> [100] 同样,<111> [110] A 代表了8个体对角线 晶向。 图1-17 立方晶格中的[100]、 [110]、[111]晶向
按照上述方法确定的简立方晶格的晶向如图所示, [111 ] [110 ] [100 ] [010 ] [001 ] 晶向指数和坐标系的 选取有关,OA的反方 向记做 ,由于 立方晶格的对称性, 沿立方边的 6个晶向 是等价的,记做: ⎡ ⎤ 100 ⎣ ⎦ [100 , 100 , 010 , 010 , 001 , 001 ] ⎡ ⎤ ⎡⎤ ⎡⎤ [ ] [ ] ⎣ ⎦ ⎣⎦ ⎣⎦ < 100 > 同样, 代表了 8个体对角线 晶向。 < > 111

[001] [010] [i00] [1i1] []111 [100] [010] [i1i] [oo1] [1i] 图1-18[100]及其等效晶向 图1-19[111]及其等效晶向 [101][i01] [i10] [110] [011] [01i] 图1-20[110]及其等效晶向

晶体点阵的所有格点也可以看成是排列在一系列相互平行、 等间距的平面系上,这些平面叫晶面,很明显,对每个晶面系来 说,格点在各晶面中的分布是相同的;一个晶面系必须包含所有 格点,晶格中可以有很多个(严格说是无穷个)晶面系。以后讨 论晶体的性质时常要指出具体晶面,因此需要确定晶面系的名 称一晶面指数。 晶面指数的一般确定方法: 1.在一组相互平行的晶面中任选一个晶面,量出它在三个坐标 轴上的截距并用点阵周期a,b,c为单位来量度; 2.写出三个截距的倒数,和一个坐标轴平行、截距为∞时,倒 数记做零; 3.将三个倒数分别乘以分母的最小公倍数,把它们化为三个简 单整数,并用圆括号括起,即为该组平面系的晶面指数。 这种方法定义出的晶面指数也叫“密勒(Miller)指数
晶体点阵的所有格点也可以看成是排列在一系列相互平行、 等间距的平面系上,这些平面叫晶面,很明显,对每个晶面系来 说,格点在各晶面中的分布是相同的;一个晶面系必须包含所有 格点,晶格中可以有很多个(严格说是无穷个)晶面系。以后讨 论晶体的性质时常要指出具体晶面,因此需要确定晶面系的名 称——晶面指数。 晶面指数的一般确定方法: 1. 在一组相互平行的晶面中任选一个晶面,量出它在三个坐标 轴上的截距并用点阵周期a,b,c为单位来量度; 2. 写出三个截距的倒数,和一个坐标轴平行、截距为∞时,倒 数记做零; 3. 将三个倒数分别乘以分母的最小公倍数,把它们化为三个简 单整数,并用圆括号括起,即为该组平面系的晶面指数。 这种方法定义出的晶面指数也叫 “密勒(Miller)指数 ”
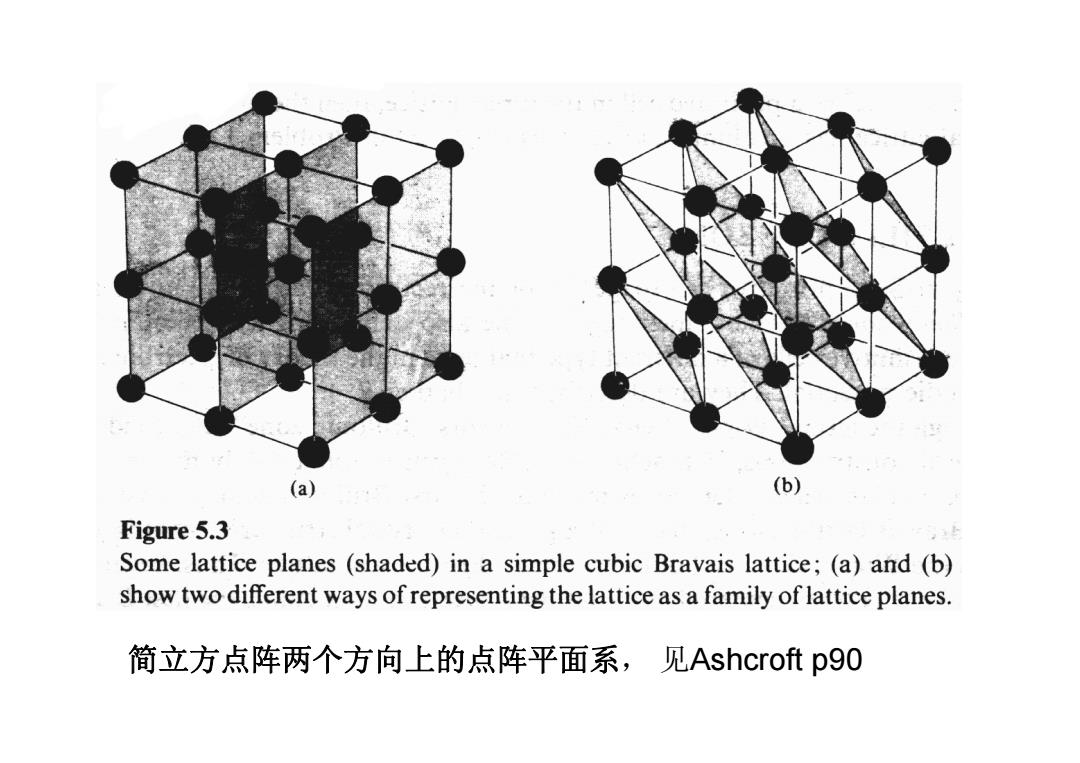
(a) (b) Figure 5.3 Some lattice planes (shaded)in a simple cubic Bravais lattice;(a)and (b) show two different ways of representing the lattice as a family of lattice planes. 简立方点阵两个方向上的点阵平面系,见Ashcroft p9O
简立方点阵两个方向上的点阵平面系, 见Ashcroft p90