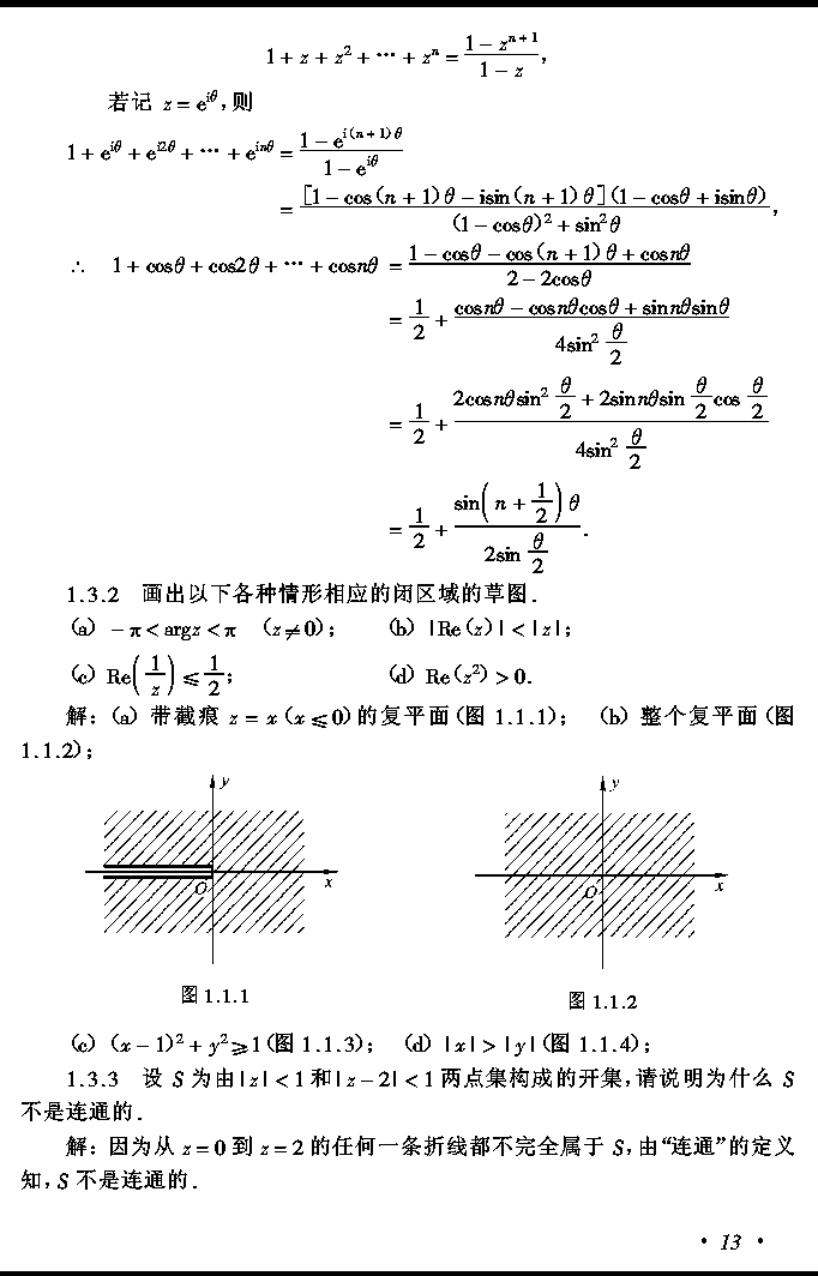
1+名+2+…+x”= 1-zn+1 1-x, 若记x=e说,则 1+e9+e20+…+e0=1-ea+00 1-e的 =[1-cos (n+1)0-isin (n+1)0](1-cos0+isine) (1-cos8)2+sir20 .1+60s8+coe20+…+co6nd=1-c0s日-c0s(n+1)日+c0sr0 2-2cos0 1 cosne-cosndcose+sinndsing 4sin? 2 2 2conin号+2 in号cas 2 4r号 ma+9 2sin 2 1.3.2画出以下各种情形相应的闭区域的草图. (a)-π<rgx<π(x≠0); (b)IRe (z)I<Izl; wd(H)s d)Re(x2>0. 解:(a)带截痕x=x(x≤0)的复平面(图1.1.1);(b)整个复平面(图 1.1.2); 图1.1.1 图1.1.2 (c)(x-1)2+y2≥1(图1.1.3):(d1x1>1y1(图1.1.40; 1.3.3设S为由|x1<1和1x-21<1两点集构成的开集,请说明为什么S 不是连通的. 解:因为从x=0到x=2的任何一条折线都不完全属于S,由“连通”的定义 知,S不是连通的. ·13·

图1.1.3 图1.1.4 1.42求函数g)=立+户=+i的定义域并正明当>0,ly川 <1时, g(z)=f(x), 这里f)=小6+迈y 解:函数g(x)的定义域为:x≠0且y≠1 ”f0=小6+=y引+子 (x>0,lyl<1), .当x>0且1yl<1时,f(z)=g(z). 1.4.3写出函数f(z)=z2+x+1的f(x)=u(x,y)+iw(x,y)形式. 解:f(z)=(x+iy)3+x+y+1 =x3-392+x+1+i(y+3x2y-y2). 1.4.4设f(z)=x2-y2-2y+i2x+2y),写出f()关于x的表达式. 解:f(z)=x2-y2+2刘yi+2xi-2y=(x+iy)2+2i(x+iy) =x2+2ix. 1.5.2求x的值()e2=-2;b)e=1+N3i;(@)e2-1=1. 解:(ae+iy=2e2&+Dd, ∴.x=2,y=2k+1)π .名=n2+2k+1)i(k=0,±1,±2,…): 06)62+y=2e3+24元, x=h2,y=(2k+3)x :=h2+(2k+号)a (k=0,±1,±2,) (c)'2x-1=In1=n1+2kxi, ·14

1 .名= +k元(k=0,±1,±2,). 1.5.3证明:1e1≤e 证:1e1=1e2-y*2i1=e2-,e=e+y, le"lela 1.5.4证明:1e21<1当且仅当Re(x)>0. 证:1e2|=e2z, .当Re(z)=x>0时,le2a1<1. 反之,要想1ea1<1,需x=Re()>0. .1e-2a1<1当且仅当Re(z)>0. 1.5.5证明:(a)e=e b)e=e当且仅当x=kπ(k=0,±1,±2,…). 证:(a)e=e-iy=e(cosy-isiny)=e2(cosy+iiny)=e. (b)eiei,eirei, '.-名=名+2kπ? .名=kπ(k=0,±1,±2,…). 反之,当x=kπ时. e=ei=(-1)k, e=e=(-10, .e=e, .e=e当且仅当x=kπ(k=0,±1,±2,…). 1.5.6a)若e为纯虚数,x有什么限制? )证明:若e2为实数,则Im(x)=kx(k=0,±1,±2,…). 证:(a)当e=e(cosy+siny)为纯虚数时, c0$y=0: m()=k领+受 (k=0,±1,±2,…) b)设名=x+iy,则当e2=e2(cosy+iiny)为实数时, siny =0, ..m(z)=kπ (k=0,±1,±2,…). 1.57证明:0h1-)=2m-年i Ln(-1+3=h2+2(k+)i4=0,±1,±2,…). 证:0h1-D=n2-年i=恤-平: ·15·

n(-1+3D=2+号d+2k对 =m+2(k+号)冠k=0,±1,±2,…). 1.5.11证明:若Re(x)>0,Re(x2)>0,那么 In (12)=Iz +Inz2. 证:由1.1.22知Re(x1)>0,Re(x2)>0时, ag(名12)=ar%名+ag22? nlx12l=nl名l+nl2l, ∴.n1z2=nlz12|+iarg(x1z2) =Inl z11 +Inl z2l +i(argz1+argz?) =Inz+lnz2- 1.5.13 应用A》=Ag1-Ag,证明: Inz -Inz2. 证: -h+ Inlzl -Il zl iArgz1-iArgz2 Lnz1 Lnz2, ·.结论成立. 1.5.14证明:当九=0,±1,±2,…时, (a)(1+i)i=e-平+2ade2; )(-1D=e2. 证:(a)1+)=ea+0=e0a2+香i+2a=e-吾+2aweh2; )(-D片=e-D=ea+Di=e24(n≠0,k=0,±1,±2,). 1.5.15求值:()(1-D;( )[受(-1-3D]. 解:(a)(1-)f=e4m1-=ea5-i+2k8=er-8kne2h2; 0)[受(-1-3d]3-6-1-50-e(1-3+2) =-e-60x2 1.5.16由=e证明:(-1+V3)7=±22. 证:(-1+V3)2=e2(-1+5)=e(恤+i+2)=ed+3mea =±22. ∴ 等式成立. 1.5.17 证明:若x≠0,a为实数,那么11=e=1z. 证:,2=eLas=ea (lal+inrgs+2kD, ·16·

.1zl=eelalal =lzla. 1.5.18令c,d和x(x≠0)为复数,若所有的幂均取主值,证明: 0 (b)2d=f+d. 证:(a)xxe=elaa·ecLm=e=1, 1 0b)zx4=e·ea=eo+》am=ze+d. 1.5.19证明:e=cosx+inz. 正:”右边=兰+世=产=左边, 2 2i 等式成立. 1.5.20(0证明:2sin(名1+z2)sin(x1-2)=coe22-cos2x1- 证:,2sin(x1+x2)sin(x1-z2) =2e9*y-。8+y,69yi-66-y 2i 2i =6231-624-64+624: -2 =c0s2x2-c0e21 等式成立 1.5.20中的(a~(e),(g可类似证之. 1.5.21证明:|sinx2=inx+sh2y,并进而推出Isinz|≥IsinI. 证:,inx=sinxcosiy+cosxsiniy=sinzchy+icosxshy, .'Isinz12=(sinxchy)2+(cosxshy)2=sin2x+sh2y, .IsinzI≥Isinx I. 1.5.22 证明:Ishyl≤I sinz I≤chy;Ishyl≤IcoszI:≤chy. 证:由上题 sin2x+sh2y Isinz 12=ch2y-cos2x, Ishyl≤Isinz l≤chy. 同理|shyl≤IcoszI≤chy. 1.5.23 证明:cex-0当且仅当x-(k+之)x,其中名为整数. 证::cosx=cosxchy-isinxshy=0, cosx=0且shy=0, g=x+iy=(k+2)x (k=0,±1,±2,…). 以上过程可逆,故结论成立. ·17·