
导航 解:在△ABC中,AC=400m,BC=600m,∠ACB=60°. 由余弦定理,得AB2=AC2+BC2-2 4C.BC.c0s60°, 则AB= 4002+6002-2×400×600×7≈529.2(m, 所以DE=AB-AD-BE≈409.2(m). 即隧道DE的长约为409.2m
导航 解:在△ABC中,AC=400 m,BC=600 m,∠ACB=60° . 由余弦定理,得AB2=AC2+BC2 -2AC·BC·cos 60° , 所以DE=AB-AD-BE≈409.2(m). 即隧道DE的长约为409.2 m. 则 AB= 𝟒𝟎𝟎𝟐 + 𝟔𝟎𝟎𝟐-𝟐 × 𝟒𝟎𝟎 × 𝟔𝟎𝟎 × 𝟏 𝟐 ≈529.2(m)

导航 延伸探究 本例中,若已知角B,C及BC,AD,BE的值,能否求DE的长? 提示:能A=π-B-C, 由BC=AB sinA 求出AB, .∴.DE=AB-AD-BE
导航 本例中,若已知角B,C及BC,AD,BE的值,能否求DE的长? 提示:能.∵A=π-B-C, ∴DE=AB-AD-BE. 由 𝑩𝑪 𝐬𝐢𝐧𝑨 = 𝑨𝑩 𝐬𝐢𝐧𝑪 ,求出 AB

导航 反思感悟 在解决实际问题时,先将实际问题转化为平面几何问题,再将 已知条件转化为三角形中的边角问题,最后利用正、余弦定 理解三角形
导航 在解决实际问题时,先将实际问题转化为平面几何问题,再将 已知条件转化为三角形中的边角问题,最后利用正、余弦定 理解三角形
导航 【变式训练1】如图,在河岸边有一点A,河对岸有一点B,要测 量A,B两点间的距离,先在岸边取基线AC,测得AC=120m, ∠BAC=45°,∠BCA=75°,求A,B两点间的距离: B A C
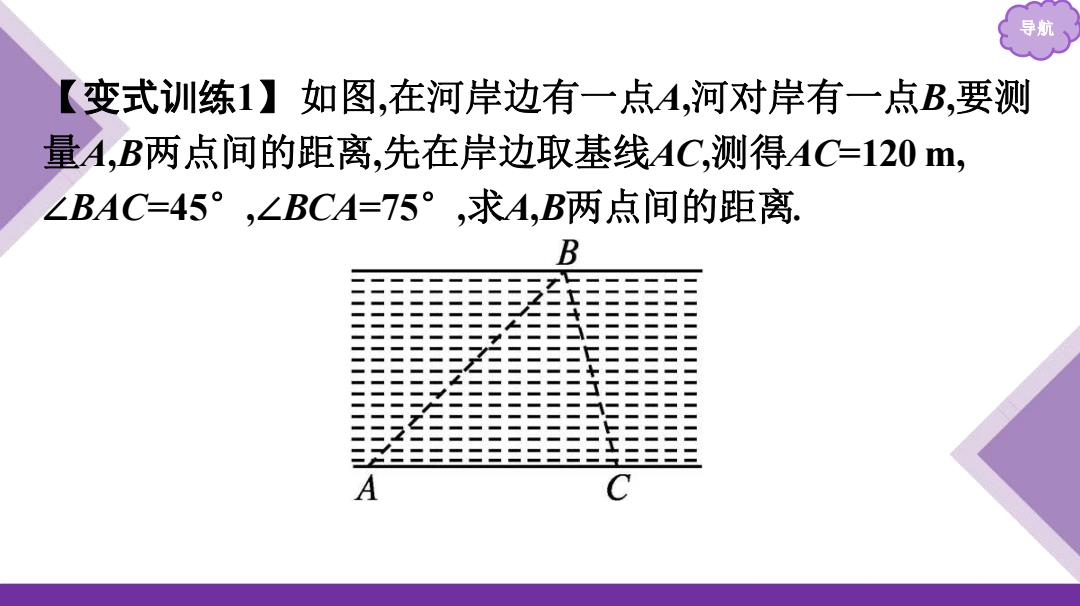
导航 【变式训练1】如图,在河岸边有一点A,河对岸有一点B,要测 量A,B两点间的距离,先在岸边取基线AC,测得AC=120 m, ∠BAC=45° ,∠BCA=75° ,求A,B两点间的距离

导航 解:在△ABC中,AC=120m,∠BAC=45°,∠BCA=75°, 则∠ABC=180°-(∠BAC+∠BCA)=60°, 由正弦定理,得 AB AC in∠BCA sinzABC' 则AB=-120sin75°-203V2+V6. sin60° 即A,B两,点间的距离为203V2+V6)m
导航 解:在△ABC中,AC=120 m,∠BAC=45° ,∠BCA=75° , 则∠ABC=180°-(∠BAC+∠BCA)=60° , 由正弦定理,得 𝑨𝑩 𝐬𝐢𝐧∠𝑩𝑪𝑨 = 𝑨𝑪 𝐬𝐢𝐧∠𝑨𝑩𝑪 , 则 AB=𝟏𝟐𝟎𝐬𝐢𝐧𝟕𝟓° 𝐬𝐢𝐧𝟔𝟎° =20(3 𝟐 + 𝟔). 即 A,B 两点间的距离为 20(3 𝟐 + 𝟔)m