
●注 1.定理的条件是重要的 (1)条件不满足结论有可能不成立 (2)条件不满足结论也有可能成立 x2 x<1 例f(x)= 0 -2≤x≤-1 1 1≤x≤2 2.定理的条件是充足的 例f(x)=V1-x2
⚫注 1.定理的条件是重要的 (1)条件不满足结论有可能不成立 (2)条件不满足结论也有可能成立 − − = 1 1 2 0 2 1 1 ( ) 2 x x x x 例 f x x y o 2.定理的条件是充足的 例 2 f (x) = 1− x x y o

微分中值定理 罗尔定理 二、 拉格朗日中值定理 三、柯西中值定理 四、中值定理的应用
微分中值定理 一、罗尔定理 二、拉格朗日中值定理 三、柯西中值定理 四、中值定理的应用

微分中值定理 罗尔定理 二、 拉格朗日中值定理 三、柯西中值定理 四、中值定理的应用
微分中值定理 一、罗尔定理 二、拉格朗日中值定理 三、柯西中值定理 四、中值定理的应用
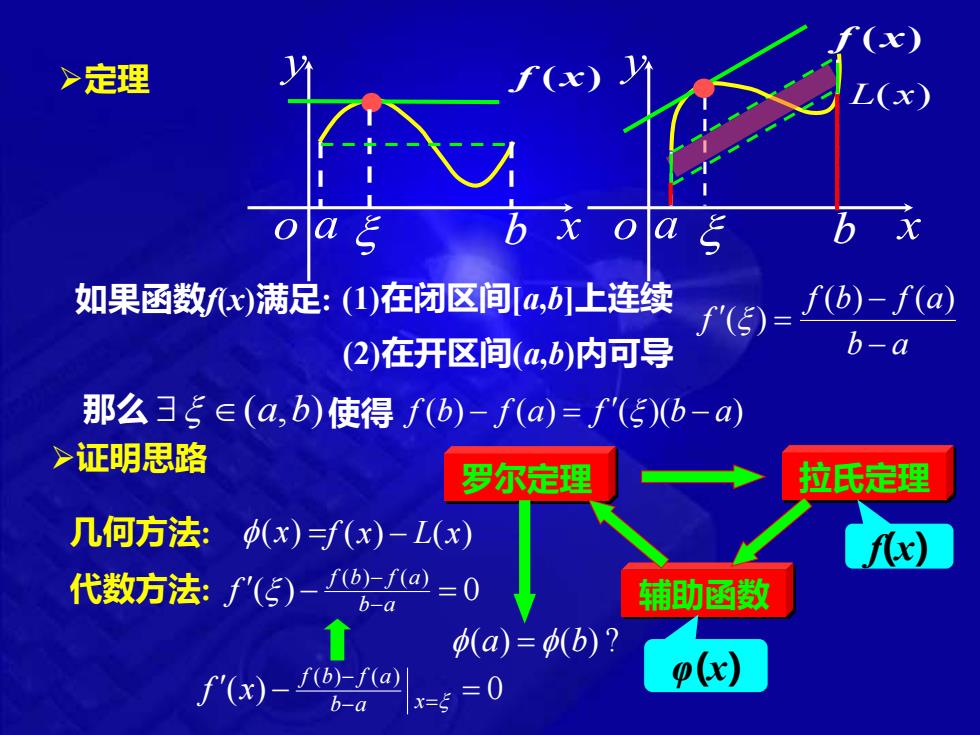
>定理 (x) (x) b x oag b x 如果函数fx)满足:(1)在闭区间a,b]上连续 f5)=6-1a) (2)在开区间(4,b)内可导 b-a 那么35∈(a,b)使得f(b)-f(a)=f'(5)b-a) >证明思路 罗尔定理 拉氏定理 几何方法: (x)=f(x)-L(x) fx) 代数方法:f(5)-1@=0 b-a 辅助函数 (a=b)? f(x)-1(b)-f(a) =5=0 p() b-a
a b x y o f (x) x y o a b f (x) 如果函数f(x)满足: ➢定理 (1)在闭区间[a,b]上连续 (2)在开区间(a,b)内可导 ➢证明思路 罗尔定理 拉氏定理 辅助函数 f(x) φ(x) (a) =(b) ? L(x) 几何方法: (x) =f (x) − L(x) 代数方法: ( ) 0 ( ) ( ) − = − − b a f b f a f ( ) 0 ( ) ( ) − = = − − b a x f b f a f x b a f b f a f − − = ( ) ( ) ( ) 那么 (a,b) 使得 f (b) − f (a) = f ()(b − a)