《产业经济学》课程教学资源（文献资料）现代产业经济学前沿问题研究（编著：臧旭恒、林平）

格竞争，找到产业内贸易存在的条件呢？答案应该是背定的。我们可设本国企业和外国企业 的直接需求函数分别是(P,P2)和q(P,P2)。但是，可能无法像同质产品数量竞争情况 那样，得到具体而确切的结果 我们猜测，是否有一种简单的办法解决这个问题，也就是引入Dxt二次效用函数 U=Mg,42)+M 其中4q,94)=a,4,+a,2-(/2(B,q+2g,92+B,g)。1这样，我们就能够以一种 简单而系统的方法把数量竞争和价格竞争纳入一个统一的框架来讨论，这是我们下一步的工 作之一. (四)战略性贸易政策 衣业，的贸我是国材风 强调了利润转移效应和反托拉剪 业的激励 为我们假设政府可 这等价 在模型化相是项政策 慢的。政策的不易变更性正好给了政府做出承诺的技术和力量。第二，政府有很多事情要做 它要制定各种贸易政策，而且，它要制定除了贸易政策外的其它政策，因此，它要维持自己 的声誉，保证政策的实施。刘 (一)战略性出口贸易政策 rander& SP 1985)开创了战略性出口贸易政策的研究。他们考虑了这样一个模型 存在 个国家 ,第三国是消费国 本国和外国分别有一家企业生产该产品，它们被称为本国企业和外国企业。我们假设它们的 产品是无差别替代品。假设它们具有非递增规模收益的生产技术，分别可以总结为成本函数 C(q)和C2(q)。假定本国企业和外国企业的产品全部出口到第三国，没有国内消费，第 三国市场上的逆需求函数（价格）是p(q,+2)。 生产国不消费所考虑的产品，而是向第三国出口。这是Brander&Spencer所做出的一 个异常聪明的简化工作。这样，每一个企业生产的边际成本就是它使用的资源的社会成本。 结果，对于每一个生产国而言，它的福利等同于企业的利润。” 考虑一 个两阶段对策。在第 本国政府制定单位出口补贴·在 制定补贴时 它知道市场需求与企业（包括外国企业）成本的函数形式，并且还知道补贴制定之后企业的竞 争类型为何，同时，补贴是可以公开观测的 在第二个阶段，两个企业进行Coumot(数量)竞争，给定外国企业观测到本国政府制定 的出口补贴。 下面，我们运用逆向归纳法解这个对策 给定本国的出口补贴，本国企业在给定外国企业产量的条件下，选择产量最大化自己的 利润。 0 见Dixi(1979) 克g27它的鞋7 2

21 格竞争，找到产业内贸易存在的条件呢？答案应该是肯定的。我们可设本国企业和外国企业 的直接需求函数分别是 ( , ) 1 2 1 q p p 和 ( , ) 1 2 2 q p p 。但是，可能无法像同质产品数量竞争情况 那样，得到具体而确切的结果。 我们猜测，是否有一种简单的办法解决这个问题，也就是引入 Dixit 二次效用函数 U  u(q1,q2 )  M 其中 ( , ) (1 2)( 2 ) 2 1 2 2 2 2 u q1 q2 1q1 2q2  1q1  q q   q 。19这样，我们就能够以一种 简单而系统的方法把数量竞争和价格竞争纳入一个统一的框架来讨论。这是我们下一步的工 作之一。 （四）战略性贸易政策 以寡头竞争为导向的贸易政策，也就是战略性贸易政策强调了利润转移效应和反托拉斯 效应。但是，贸易政策之所以能够起到这样的作用，是因为我们假设政府可以在国际竞争之 中做出承诺，影响企业的激励。这等价于我们在模型化相关的动态对策时，赋予政府先行动 的地位。这个假设的依据是，第一，官僚机构缺乏效率。某项政策一旦制定，调整起来是缓 慢的。政策的不易变更性正好给了政府做出承诺的技术和力量。第二，政府有很多事情要做， 它要制定各种贸易政策，而且，它要制定除了贸易政策外的其它政策，因此，它要维持自己 的声誉，保证政策的实施。20 （一）战略性出口贸易政策 Brander & Spencer(1985)开创了战略性出口贸易政策的研究。他们考虑了这样一个模型。 存在三个国家，本国、外国和第三国。本国和外国是某种产品的生产国，第三国是消费国。 本国和外国分别有一家企业生产该产品，它们被称为本国企业和外国企业。我们假设它们的 产品是无差别替代品。假设它们具有非递增规模收益的生产技术，分别可以总结为成本函数 ( ) 1 1 c q 和 ( ) 2 2 c q 。假定本国企业和外国企业的产品全部出口到第三国，没有国内消费，第 三国市场上的逆需求函数(价格)是 ( ) 1 2 p q  q 。 生产国不消费所考虑的产品，而是向第三国出口。这是 Brander & Spencer 所做出的一 个异常聪明的简化工作。这样，每一个企业生产的边际成本就是它使用的资源的社会成本。 结果，对于每一个生产国而言，它的福利等同于企业的利润。21 考虑一个两阶段对策。在第一个阶段，由本国政府制定单位出口补贴 s 。在制定补贴时， 它知道市场需求与企业(包括外国企业)成本的函数形式，并且还知道补贴制定之后企业的竞 争类型为何，同时，补贴是可以公开观测的。 在第二个阶段，两个企业进行 Cournot(数量)竞争，给定外国企业观测到本国政府制定 的出口补贴。 下面，我们运用逆向归纳法解这个对策。 给定本国的出口补贴，本国企业在给定外国企业产量的条件下，选择产量最大化自己的 利润。 19 见 Dixit(1979)。 20 见 Spencer & Brander(1983, p.711)和它的脚注 7. 21 见 Krugman(1989, p.1202)

maxT'(9,4:)=pg+94,-c(g,)+sq, 日标最大化的一阶条件是 II'=pq+p-ci+s=0 相似地，外国企业在给定本国企业产量的条件下，选择产量，最大化它的利润。 m8xΠ'(g,9)=pgi+924-6g,) 目标最大化的一阶条件是 =pq42+p-c2=0 从这两个一阶条件之中，我们可以解出第二阶段子对策的Nash均衡， 贸易政策的效应是怎样的？我们假设数量是战略替代的 Π2=pg+p<0:=pg2+p<0 也就是，企业的边际收益随着竞争对手产量的增加而减少。两个企业利润最大化的一阶条件 对s求导数，得到 0+n,+m,=0 器+器=0 ds 写成矩阵方程的形式 品 显然，系数矩阵的行列式为D>0.应用克菜姆法则，我们得到 q,/as=-Π2/D>0 aq2/6s=Π3/D<0 现在，回到对策的第一个阶段，我们要回答什么是本国政府最优的贸易政策选择。由于 本国的产品全部出口到第三国市场，因此，本国福利就是本国企业利润减去补贴成本 W'(q,(s,92(ss)=T'(q(s),92(ss)-sq 目标函数最大化的一阶条件是 mg=Π；4+Π-q-=0 ds ds 在这里，我们运用了包络定理(EnvelopeTheorem)。从中可以解出 层 因此，在我们考虑的模型之中，给定企业的选择是战略替代的，那么，本国最优的贸易 ”注意，=p<0

22 1 2 1 2 1 1 1 1 1 { } max ( , ; ) ( ) ( ) 1 q q s p q q q c q sq q      目标最大化的一阶条件是 0 ' 1 1 1 ' 1  p q  p  c  s  相似地，外国企业在给定本国企业产量的条件下，选择产量，最大化它的利润。 max ( , ) ( ) ( ) 1 2 1 2 2 2 2 2 { }2 q q p q q q c q q     目标最大化的一阶条件是 0 ' 2 2 2 ' 2  p q  p  c  从这两个一阶条件之中，我们可以解出第二阶段子对策的 Nash 均衡。 贸易政策的效应是怎样的？我们假设数量是战略替代的 0 ' 1 1 '' 12  p q  p  ； 0 ' 2 2 '' 21  p q  p  也就是，企业的边际收益随着竞争对手产量的增加而减少。两个企业利润最大化的一阶条件 对 s 求导数，得到 0 1 1 1 2 12 1 1 11           s s q s q 0 2 2 22 2 1 21         s q s q 写成矩阵方程的形式                           0 1 2 1 2 22 2 21 1 12 1 11 q s q s 显然，系数矩阵的行列式为 D  0 . 应用克莱姆法则，我们得到 0 2 q1 s  22 D  0 2 q2 s  21 D  现在，回到对策的第一个阶段，我们要回答什么是本国政府最优的贸易政策选择。由于 本国的产品全部出口到第三国市场，因此，本国福利就是本国企业利润减去补贴成本 1 2 1 1 1 2 1 W (q (s),q (s);s)   (q (s),q (s);s)  sq 目标函数最大化的一阶条件是 0 1 1 1 2 1 2 1            s q q s s q Ws s 在这里，我们运用了包络定理(Envelope Theorem)。从中可以解出 0 1 1 2 2               q s q s s 22 因此，在我们考虑的模型之中，给定企业的选择是战略替代的，那么，本国最优的贸易 22 注意， 1 0 1 ' 2  p q 

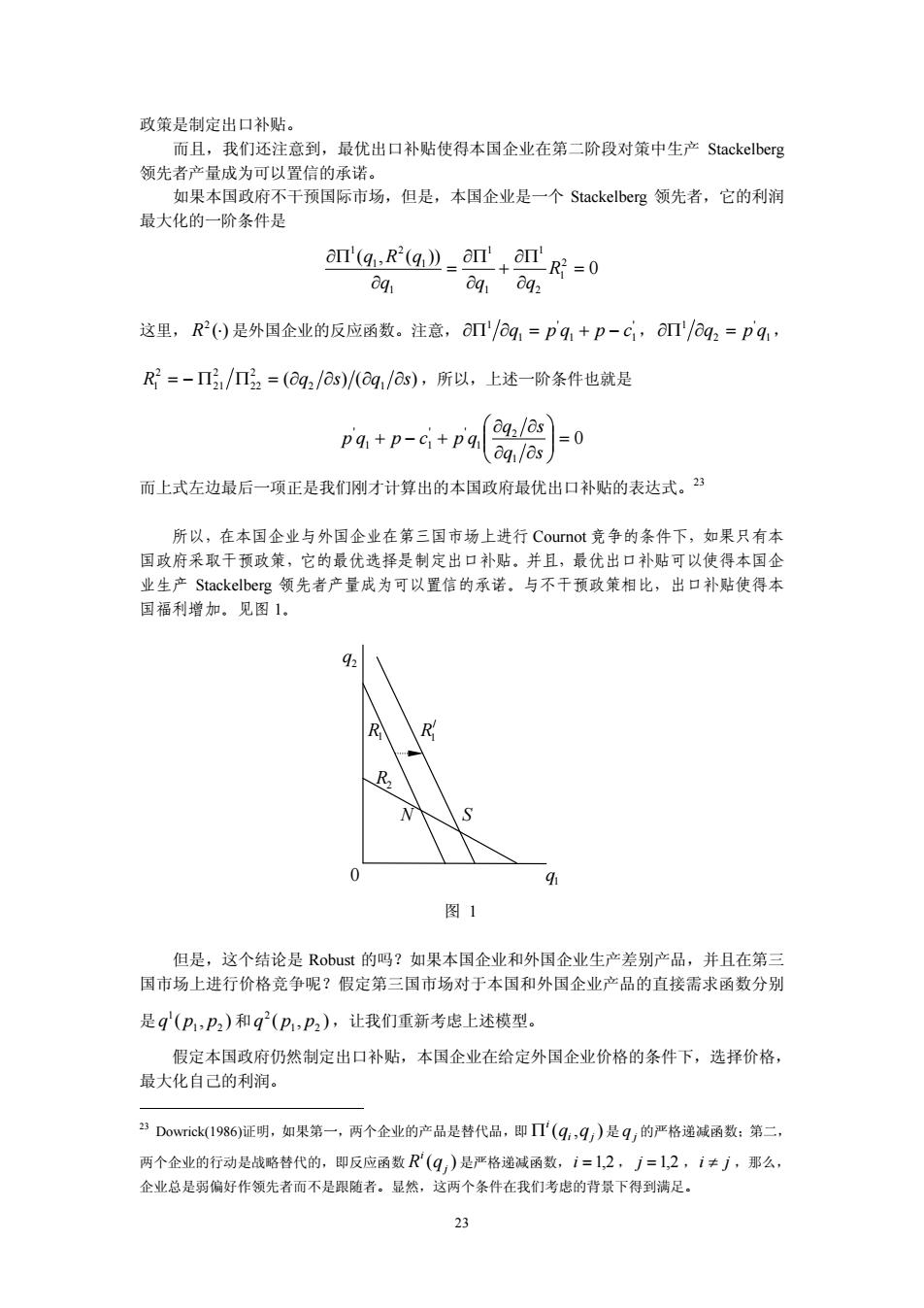
政策是制定出口补贴。 如果本国政府不干预国际市场，但是，本国企业是一个Stackelberg领先者，它的利润 最大化的一阶条件是 amg.R贮q》_an+0R=0 这里，R()是外国企业的反应函数.注意，'/g,=P9+p-C,T/q2=pq R=-Π，/2=(0q,/s)/g,/6s),所以，上述一阶条件也就是 pid+p-ci+p os) 而上式左边最后一项正是我们刚才计算出的本国政府最优出口补贴的表达式。” 所以，在本国企业与外国企业在第三国市场上进行Cournot竞争的条件下，如果只有本 国致府采取干预政第，它的最优选择是制定出口补贴。并且，最优出口补贴可以使得本国企 业生产Stackelberg领先者产量成为可以置信的承诺.与不干预政策相比，出口补贴使得本 国福利增加。见图1， 图1 但是，这个结论是Robust的吗？如果本国企业和外国企业生产差别产品，并且在第 国市场上进行价格克争呢？假定第三国市场对于本国和外国企业产品的直接需求函数分别 是q(P,P2)和q(P,P2),让我们重新考虑上述模型。 假定本国政府仍然制定出口补贴，本国企业在给定外国企业价格的条件下，选择价格， 最大化自己的利润。 ”Dowric©k(1986)证明，如果第一，两个企业的产品是替代品，即T'(q,9,)是q,的严格递减函数：第二， 两个企业的行动是战略替代的，即反应函数R(q)是严格递减函数，1=1,2，j=1,2,1≠了，那么， 企业总是弱偏好作领先者而不是跟随者。显然，这两个条件在我们考忠的背景下得到满足。 23

23 政策是制定出口补贴。 而且，我们还注意到，最优出口补贴使得本国企业在第二阶段对策中生产 Stackelberg 领先者产量成为可以置信的承诺。 如果本国政府不干预国际市场，但是，本国企业是一个 Stackelberg 领先者，它的利润 最大化的一阶条件是 0 ( , ( )) 2 1 2 1 1 1 1 1 2 1 1          R q q q q R q 这里， ( ) 2 R  是外国企业的反应函数。注意， ' 1 1 ' 1 1  q  p q  p  c ， 1 ' 2 1  q  p q ， ( ) ( ) 2 1 2 22 2 21 2 1 R      q s q s ，所以，上述一阶条件也就是 0 1 2 1 ' ' 1 1 '                q s q s p q p c p q 而上式左边最后一项正是我们刚才计算出的本国政府最优出口补贴的表达式。23 所以，在本国企业与外国企业在第三国市场上进行 Cournot 竞争的条件下，如果只有本 国政府采取干预政策，它的最优选择是制定出口补贴。并且，最优出口补贴可以使得本国企 业生产 Stackelberg 领先者产量成为可以置信的承诺。与不干预政策相比，出口补贴使得本 国福利增加。见图 1。 但是，这个结论是 Robust 的吗？如果本国企业和外国企业生产差别产品，并且在第三 国市场上进行价格竞争呢？假定第三国市场对于本国和外国企业产品的直接需求函数分别 是 ( , ) 1 2 1 q p p 和 ( , ) 1 2 2 q p p ，让我们重新考虑上述模型。 假定本国政府仍然制定出口补贴，本国企业在给定外国企业价格的条件下，选择价格， 最大化自己的利润。 23 Dowrick(1986)证明，如果第一，两个企业的产品是替代品，即 ( , ) i j i  q q 是 j q 的严格递减函数；第二， 两个企业的行动是战略替代的，即反应函数 ( )j i R q 是严格递减函数， i  1,2 ， j  1,2 ，i  j ，那么， 企业总是弱偏好作领先者而不是跟随者。显然，这两个条件在我们考虑的背景下得到满足。 2 q R1 / R1 R2 N S 0 1 q 图 1

maxΠ'(p,P2s=P9(P,P2)-c(q(p,P2》+sq(p,P2) 日标最大化的一阶条件是 Π=q+(p,-Ci+s)q=0 相似地，外国企业在给定本国企业价格的条件下，选择价格，最大化它的利润。 x(PP2)=Pq(PP:)-c((pp)) 目标最大化的一阶条件是 Π=q2+(P2-C2)q=0 从这两个一阶条件之中，我们可以解出第二阶段子对策的Nash均衡， 贸易政策的效应是怎样的？我们假设价格是战略互补的 Π2=(1-cg)g+(p,-c+s)g2>0:Π3=(1-c2gi)q+(P2-c2)qi>0 也就是，企业的边际收益随着竞争对手价格的增加而增加。两个企业利润最大化的一阶条件 对s求导数，得到 0+n,0+=0 器+器=0 ds 写成矩阵方程的形式 此腐 显然，系数矩阵的行列式为D>0.应用克菜姆法则，我们得到 p,/s=-gΠ2/D<0 aqa/as=q/D<0 现在，回到对策的第一个阶段，本国政府最大化 W'(p,(s),P2(ss)=T'(P(s,P2(ss)-sq,(P,(s),P2(s) 目标函数最大化的一阶条件是 时器-ono-倍染条}0 在这里，我们运用了包络定理(Envelope Theorem)。注意，=(p,-G+s)4·所以，从 中可以解出 s=D-c4R0<0 这里，R是外国企业的反应函数。因此，在我们考虑的模型之中，给定企业的选择是战 24

24 max ( , ; ) ( , ) ( ( , )) ( , ) 1 2 1 1 2 1 1 2 1 1 1 2 1 1 { }1 p p s p q p p c q p p sq p p p     目标最大化的一阶条件是 ( ) 0 1 1 ' 1 1 1 1 1  q  p  c  s q  相似地，外国企业在给定本国企业价格的条件下，选择价格，最大化它的利润。 max ( , ) ( , ) ( ( , )) 1 2 2 1 2 2 2 1 2 2 2 { }2 p p p q p p c q p p p    目标最大化的一阶条件是 ( ) 0 2 2 ' 2 2 2 2 2  q  p  c q  从这两个一阶条件之中，我们可以解出第二阶段子对策的 Nash 均衡。 贸易政策的效应是怎样的？我们假设价格是战略互补的 (1 ) ( ) 0 1 12 ' 1 1 1 2 1 1 '' 1 1 12   c q q  p  c  s q  ； (1 ) ( ) 0 2 21 ' 2 2 2 1 2 2 '' 2 2 21   c q q  p  c q  也就是，企业的边际收益随着竞争对手价格的增加而增加。两个企业利润最大化的一阶条件 对 s 求导数，得到 0 1 1 1 2 12 1 1 11           s s p s p 0 2 2 22 2 1 21         s p s p 写成矩阵方程的形式                           0 1 1 2 1 2 22 2 21 1 12 1 11 q p s p s 显然，系数矩阵的行列式为 D  0 . 应用克莱姆法则，我们得到 0 2 22 1 p1 s  q1  D  0 2 21 1 q2 s  q1  D  现在，回到对策的第一个阶段，本国政府最大化 ( ( ), ( ); ) ( ( ), ( ); ) ( ( ), ( )) 1 2 1 1 2 1 1 2 1 W p s p s s   p s p s s  sq p s p s 目标函数最大化的一阶条件是 ( ( ), ( )) 0 2 2 1 1 1 1 1 1 2 1 2 1 2 1                          s p p q s p p q q p s p s s s p Ws s 在这里，我们运用了包络定理(Envelope Theorem)。注意， 1 2 ' 1 1 1 2   ( p  c  s)q 。所以，从 中可以解出 ( ) 0 ( ) 2 1 1 1 1 2 ' 1 1     R q p c q s 这里， ( ) 2 R  是外国企业的反应函数。因此，在我们考虑的模型之中，给定企业的选择是战

略互补的，那么，本国最优的贸易政策是制定出口税。 而且，我们还注意到，最优出口税使得本国企业在第二阶段对策中制定Stackelberg领 先者价格成为可以置信的承诺， 如果本国政府不干预国际市场，但是，本国企业是一个Stackelberg领先者，它的利润 最大化的一阶条件是 amn,Rp业_an+tR=0 0p1 经过整理，得到 q+(p,-c)q+(p-c)4R日=0 这正是在上述政府干预对策之中，将最优出口税代入后所得到的本国企业利润最大化的一阶 条件。4 所以，在本国企业与外国企业在第三国市场上进行Bertrand竞争的条件下，如果只有本 国政府采取干预政策，它的最优选择是制定出口税。并且，最优出口税可以使得本国企业制 定Stackelberg领先者价格成为可以置信的承诺，与不干预政策相比，出口税使得本国福利 增加，见图2. 0 图2 讨 我们发现，战略性出口贸易政策对于企业事后竞争的类型是非常敏感的，如果企业的选 择是战略替代的，那么，出口补贴最优：如果企业的选择是战略互补的，那么，出口税最优。 但是，政府怎么会知道在政策制定后，企业将进行什么样的竞争呢？即本国政府面临着信息 约束。Eaton&Gr an(1986)第一次指出了这个问题。这是对战略性贸易政策的当头一椿。 到目前为止，致力于解决这个问题的 工作包括 Bagwell Staiger(199),Laussel(19 和Maggi(1996)。其中，Maggi(1996)和产业组织理论的传统最为匹配。他运用一个不完全生 产能力限制模型，比较成功地解决了信息约束的问题，他指出，产业补贴是一项总能增进本 国福利的政策。我们推荐对此有兴趣的读者去精读这篇文章。 下面简要介绍Bagwell&Staiger(1994)和Laussel(1992)的工作

25 略互补的，那么，本国最优的贸易政策是制定出口税。 而且，我们还注意到，最优出口税使得本国企业在第二阶段对策中制定 Stackelberg 领 先者价格成为可以置信的承诺。 如果本国政府不干预国际市场，但是，本国企业是一个 Stackelberg 领先者，它的利润 最大化的一阶条件是 0 ( , ( )) 2 1 2 1 1 1 1 1 2 1 1          R p p p p R p 经过整理，得到 ( ) ( ) ( ) 0 2 1 1 2 ' 1 1 1 1 ' 1 1 1 q  p  c q  p  c q R   这正是在上述政府干预对策之中，将最优出口税代入后所得到的本国企业利润最大化的一阶 条件。24 所以，在本国企业与外国企业在第三国市场上进行 Bertrand 竞争的条件下，如果只有本 国政府采取干预政策，它的最优选择是制定出口税。并且，最优出口税可以使得本国企业制 定 Stackelberg 领先者价格成为可以置信的承诺。与不干预政策相比，出口税使得本国福利 增加。见图 2。 讨论 我们发现，战略性出口贸易政策对于企业事后竞争的类型是非常敏感的，如果企业的选 择是战略替代的，那么，出口补贴最优；如果企业的选择是战略互补的，那么，出口税最优。 但是，政府怎么会知道在政策制定后，企业将进行什么样的竞争呢？即本国政府面临着信息 约束。Eaton & Grossman(1986)第一次指出了这个问题。这是对战略性贸易政策的当头一棒。 到目前为止，致力于解决这个问题的工作包括 Bagwell & Staiger(1994)，Laussel(1992) 和 Maggi(1996)。其中，Maggi(1996)和产业组织理论的传统最为匹配。他运用一个不完全生 产能力限制模型，比较成功地解决了信息约束的问题，他指出，产业补贴是一项总能增进本 国福利的政策。我们推荐对此有兴趣的读者去精读这篇文章。 下面简要介绍 Bagwell & Staiger(1994)和 Laussel(1992)的工作。 24 Dowrick(1986)证明，如果两个企业的选择是战略互补的，那么，如果一个企业偏好先行动，另外一个企 业一定偏好后行动。价格竞争条件下干预带来的结果是“双赢”的。 2 p R1 / R1 S R2 N 0 1 p 图 2