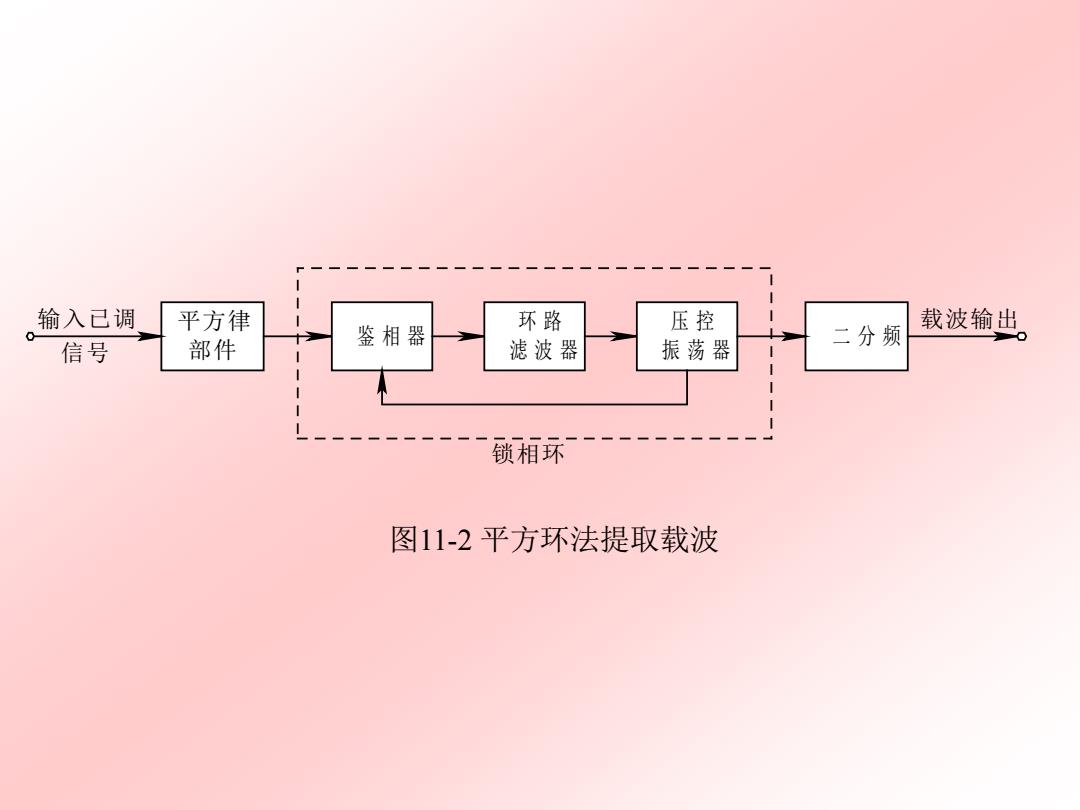
输入已调 平方律 鉴相器 环路 压控 二分频 载波输出 信号 部件 滤波器 振荡器 锁相环 图11-2平方环法提取载波
图11-2 平方环法提取载波 平方律 部件 输入已调 信号 鉴相器 二分频 环 路 载波输出 滤波器 压 控 振荡器 锁相环

当g()为矩形脉冲时,有 e=2+ C0s20t 11.2-5) 22 假设环路锁定,VCO的频率锁定在2o频率上,其输出信号为 v,)=Asin(2o.t+20) 11.2-6) 这里,0为相位差。经鉴相器(由相乘器和低通滤波器组成) 后输出的误差电压为 Va=Ka sin20 11.2-7) 式中,K为鉴相灵敏度,是一个常数。V仅与相位差有关, 它通过环路滤波器去控制压控振荡器的相位和频率,环路锁 定之后,0是一个很小的量。因此,VCO的输出经过二分频后, 就是所需的相干载波
式中,Kd为鉴相灵敏度,是一个常数。vd仅与相位差有关, 它通过环路滤波器去控制压控振荡器的相位和频率,环路锁 定之后,θ是一个很小的量。因此,VCO的输出经过二分频后, 就是所需的相干载波。 当g(t)为矩形脉冲时,有 c 1 1 e(t)= + cos2 t (11.2 - 5) 2 2 ω 0 c v (t)=Asin(2 t+2 ) (11.2 - 6) ω θ 假设环路锁定,VCO的频率锁定在2ωc频率上,其输出信号为 这里,θ为相位差。经鉴相器(由相乘器和低通滤波器组成) 后输出的误差电压为 d d v =K sin2 (11.2 - 7 θ )

应当注意,载波提取的方框图中用了一个二分频电路, 由于分频起点的不确定性,使其输出的载波相对于接收信号 相位有180°的相位模糊。相位模糊对模拟通信关系不大, 因为人耳听不出相位的变化。但对数字通信的影响就不同了, 它有可能使2PSK相干解调后出现“反向工作”的问题,克服 相位模糊度对相干解调影响的最常用而又有效的方法是对调 制器输入的信息序列进行差分编码,即采用相对移相 (2DPSK),并且在解调后进行差分译码恢复信息
应当注意,载波提取的方框图中用了一个二分频电路, 由于分频起点的不确定性,使其输出的载波相对于接收信号 相位有180°的相位模糊。相位模糊对模拟通信关系不大, 因为人耳听不出相位的变化。但对数字通信的影响就不同了, 它有可能使2PSK相干解调后出现“反向工作”的问题,克服 相位模糊度对相干解调影响的最常用而又有效的方法是对调 制器输入的信息序列进行差分编码, 即采用相对移相 (2DPSK),并且在解调后进行差分译码恢复信息

2.同相正交环法 同相正交环法又叫科斯塔斯(Costas)环,它的原理框图 如图11-3所示。在此环路中,压控振荡器(VCO)提供两路 互为正交的载波,与输入接收信号分别在同相和正交两个鉴相 器中进行鉴相,经低通滤波之后的输出均含调制信号,两者相 乘后可以消除调制信号的影响,经环路滤波器得到仅与相位差 有关的控制压控,从而准确地对压控振荡器进行调整。 设输入的抑制载波双边带信号为m(t)cos@.t,并假定环路锁 定,且不考虑噪声的影响,则VCO输出的两路互为正交的本地 载波分别为 VI=cos(@t+0) (11.2-8) V2=sin(@t+0) 式中,0为VCO输出信号与输入已调信号载波之间的相位误差
2. 同相正交环法 同相正交环法又叫科斯塔斯(Costas)环, 它的原理框图 如图 11 - 3 所示。在此环路中,压控振荡器(VCO)提供两路 互为正交的载波,与输入接收信号分别在同相和正交两个鉴相 器中进行鉴相,经低通滤波之后的输出均含调制信号, 两者相 乘后可以消除调制信号的影响, 经环路滤波器得到仅与相位差 有关的控制压控,从而准确地对压控振荡器进行调整。 设输入的抑制载波双边带信号为m(t)cosωct,并假定环路锁 定,且不考虑噪声的影响,则VCO输出的两路互为正交的本地 载波分别为 v1 = cos(ωct+θ) (11.2 - 8) v2 = sin(ωct+θ) 式中,θ为VCO输出信号与输入已调信号载波之间的相位误差
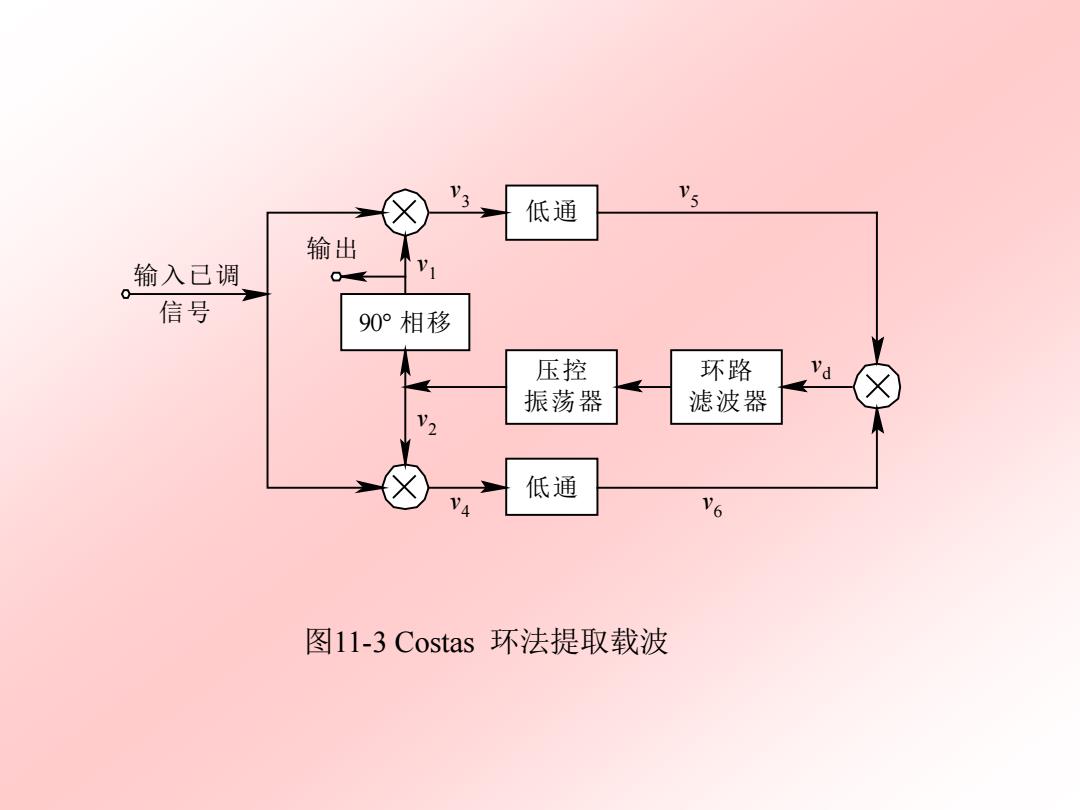
低通 输出 输入已调 信号 90°相移 压控 环路 Vd 振荡器 滤波器 V 低通 V6 图11-3 Costas环法提取载波
图11-3 Costas 环法提取载波 低通 压控 振荡器 低通 环路 滤波器 90° 相移 输出 输入已调 信号 v3 v5 v1 v2 v4 v6 vd