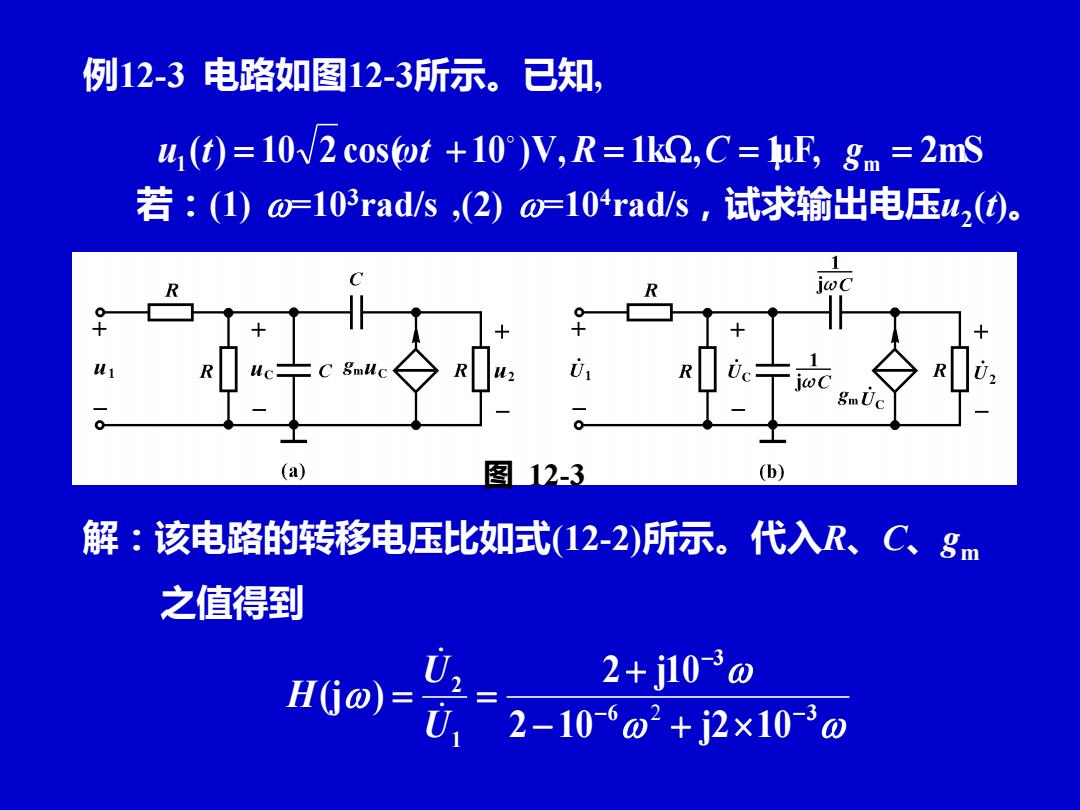
例12-3电路如图12-3所示。已知, u (t)=10v2 cos@t +10)V,R=1k2,C=lF,gm =2mS 若:(1)0103rad/s,(2)o0-104rad/s,试求输出电压42(t)。 o (a) 图12-3 (b) 解:该电路的转移电压比如式(12-2)所示。代入R、C、gm 之值得到 02= 2+j10-3o H0o)=元,=2-10-*02+j2×10'@
例12-3 电路如图12-3所示。已知, 若:(1) =103rad/s ,(2) =104rad/s,试求输出电压u2 (t)。 u1 (t) = 10 2 cos(ωt + 10 )V,R = 1k,C = 1μF, gm = 2mS 6 3 3 1 2 2 10 j2 10 2 j10 (j ) − − − − + + = = 2 U U H 解:该电路的转移电压比如式(12-2)所示。代入R、C、gm 之值得到 图 12-3

(1)w=103rad/s时 U2 HG0)=U, 2+i1=1∠-36.9 1+j2 由式(12-6)求得 u2(t)=H(j@)Uim coslat+v+0(@)] =1×10W2c0s103t+10°-36.9)V =10√2cos103t-26.9)V (2)0-104rad/s时 0= 2+j10 HG@)=U=-98+j20 =0.102∠-89.8
(1) =103rad/s时 1 36.9 1 j2 2 j1 (j ) 1 2 = − + + = = U U H 由式(12-6)求得 10 2 cos(10 26.9 )V 1 10 2 cos(10 10 36.9 )V ( ) | (j )| cos[ ( )] 3 3 2 1m 1 = − = + − = + + t t u t H U t (2) =104rad/s时 0.102 89.8 98 j20 2 j10 (j ) 1 2 = − − + + = = U U H

由式(12-6求得 u,(t)=H(j@)Uim coslat+v+e(@)] =0.102×102c0s104t+10°-89.8°)V =1.02/2c0s104t-79.8)V 实际电路的网络函数,可以用实验方法求得。将正弦 波信号发生器接到被测网络的输入端,用一台双踪示波器 同时观测输出和输入正弦波。从输出和输入波形幅度之比 可求得求得转移电压比的H(G⊙)儿。从输出和输入波形的相 位差可求得⊙)。改变信号发生器的频率,求得各种频率 下的网络函数H(G⊙),就知道该网络的频率特性
由式(12-6)求得 1.02 2 cos(10 79.8 )V 0.102 10 2 cos(10 10 89.8 )V ( ) | (j )| cos[ ( )] 4 4 2 1m 1 = − = + − = + + t t u t H U t 实际电路的网络函数,可以用实验方法求得。将正弦 波信号发生器接到被测网络的输入端,用一台双踪示波器 同时观测输出和输入正弦波。从输出和输入波形幅度之比 可求得求得转移电压比的|H(j)|。从输出和输入波形的相 位差可求得()。改变信号发生器的频率,求得各种频率 下的网络函数H(j),就知道该网络的频率特性

四、网络函数的频率特性 网络函数是一个复数,用极坐标形式表为 H(Go)HGo)∠(o) 一般来说,网络函数的振幅H(Go)和相位(o)是频率 的函数。可以用振幅或相位作纵坐标,画出以频率为横坐 标的幅频特性曲线和相频特性曲线。由幅频和相频特性曲 线,可直观地看出网络对不同频率正弦波呈现出的不同特 性,在电子和通信工程中被广泛采用
四、网络函数的频率特性 H(j) =| H(j)| () 一般来说, 网络函数的振幅|H(j)|和相位()是频率 的函数。可以用振幅或相位作纵坐标,画出以频率为横坐 标的幅频特性曲线和相频特性曲线。由幅频和相频特性曲 线,可直观地看出网络对不同频率正弦波呈现出的不同特 性,在电子和通信工程中被广泛采用。 网络函数是一个复数,用极坐标形式表为
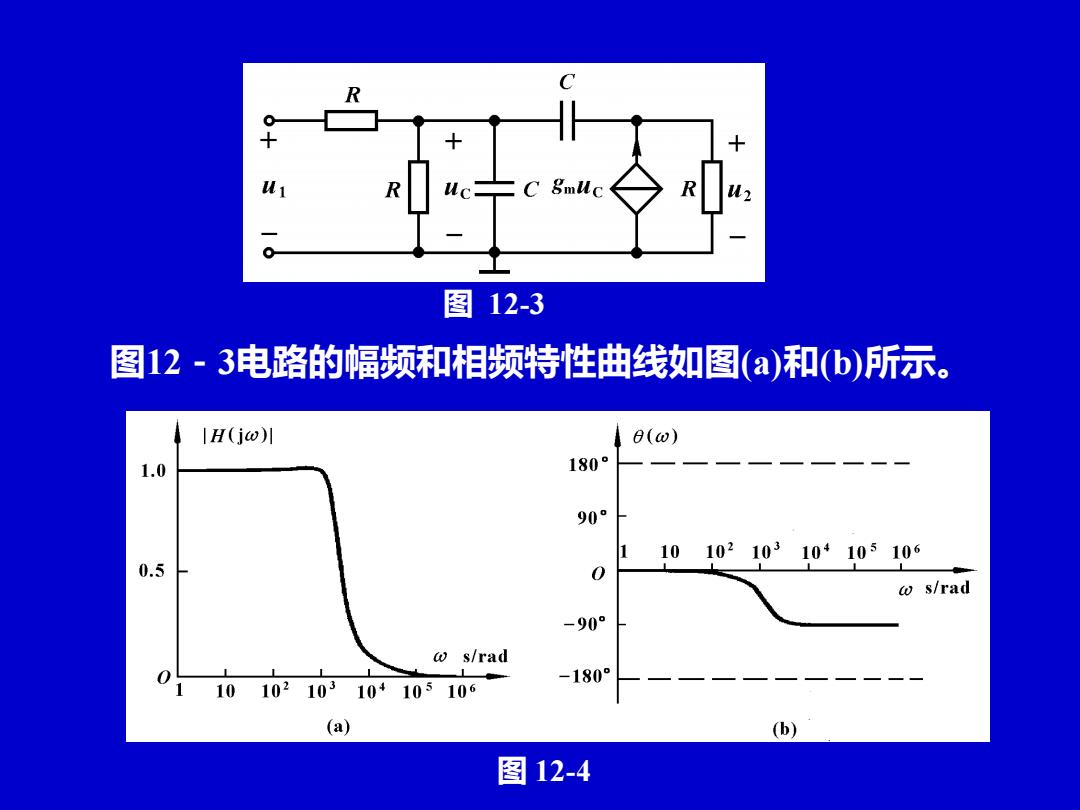
C R R Wc= C 8muc 图12-3 图12-3电路的幅频和相频特性曲线如图(a)和(b)所示。 |H(jw)川 6(o) 1.0 180° 90 1 10102103104105106 0.5 0 w s/rad -90° w s/rad 1010210310+105106 -180° (a) (b) 图12-4
图 12-3 图12-3电路的幅频和相频特性曲线如图(a)和(b)所示。 图 12-4