内蒙古科技大学：《材料力学》课程PPT教学课件（土木类）第十一章 能量法

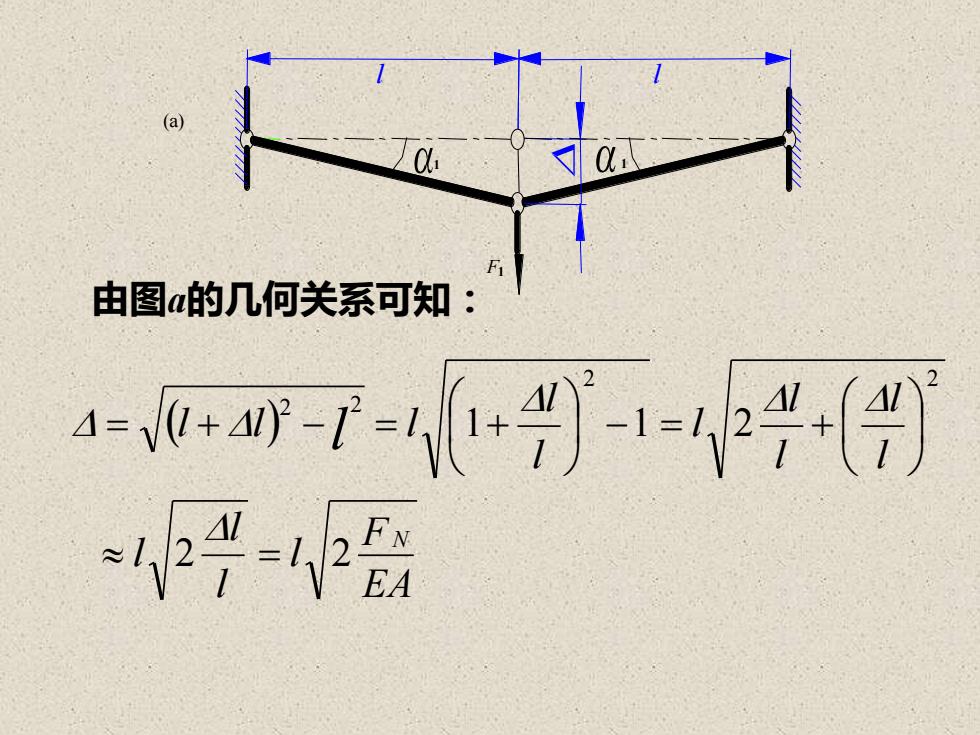
7F由图α的几何关系可知：-0+---1)1

( ) E A F l l l l l l l l l l l l l l N l 2 2 1 1 2 2 2 2 2  =        − = +      = + − = +       由图a的几何关系可知： F1 1 1 l l (a)

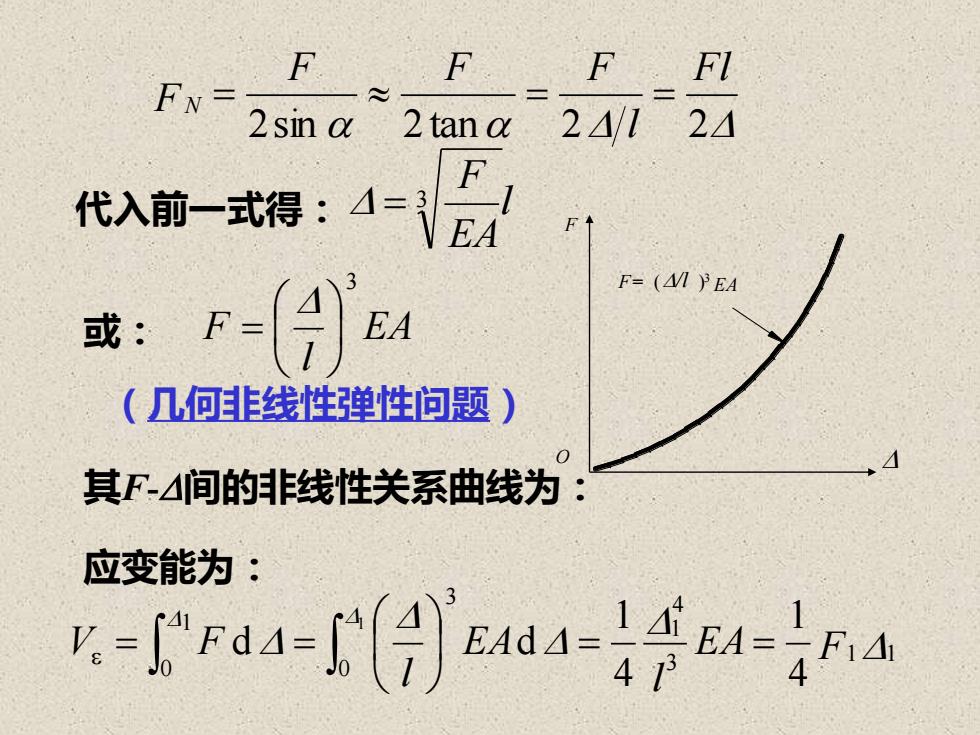
FFFFIFN2 sin α2124/12 tan αF代入前一式得：4=EAF= (M PEAAEA或：F一一1（几何非线性弹性问题其F-4间的非线性关系曲线为：应变能为：V-I"F4-T()EAd-EA-F14

2sin  2 tan 2 2 Fl l F F F F N =  = = 代入前一式得： l EA F  = 3 或： EA l F 3       =  （几何非线性弹性问题） 其F-间的非线性关系曲线为： 应变能为：        1 1 3 4 1 0 3 1 0 4 1 4 1 d d 1 EA F l EA l V F  = =      = =    F F= ( ) EA 3 O  /l

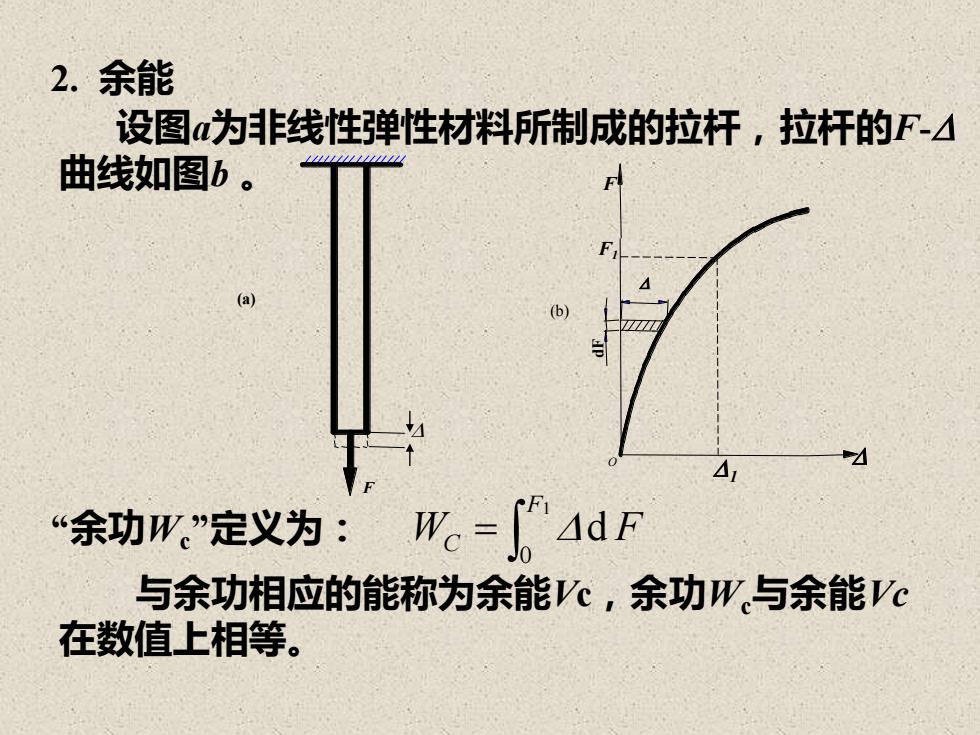
2.余能设图a为非线性弹性材料所制成的拉杆，拉杆的F-曲线如图b。F414dF“余功w"定义为：W。=[与余功相应的能称为余能Vc，余功W.与余能Vc在数值上相等

2. 余能 设图a为非线性弹性材料所制成的拉杆，拉杆的F- 曲线如图b 。 “余功Wc ”定义为：  = F WC F 1 0 d 与余功相应的能称为余能Vc，余功Wc与余能Vc 在数值上相等。 F (a)  F O dF  1 F1  (b)

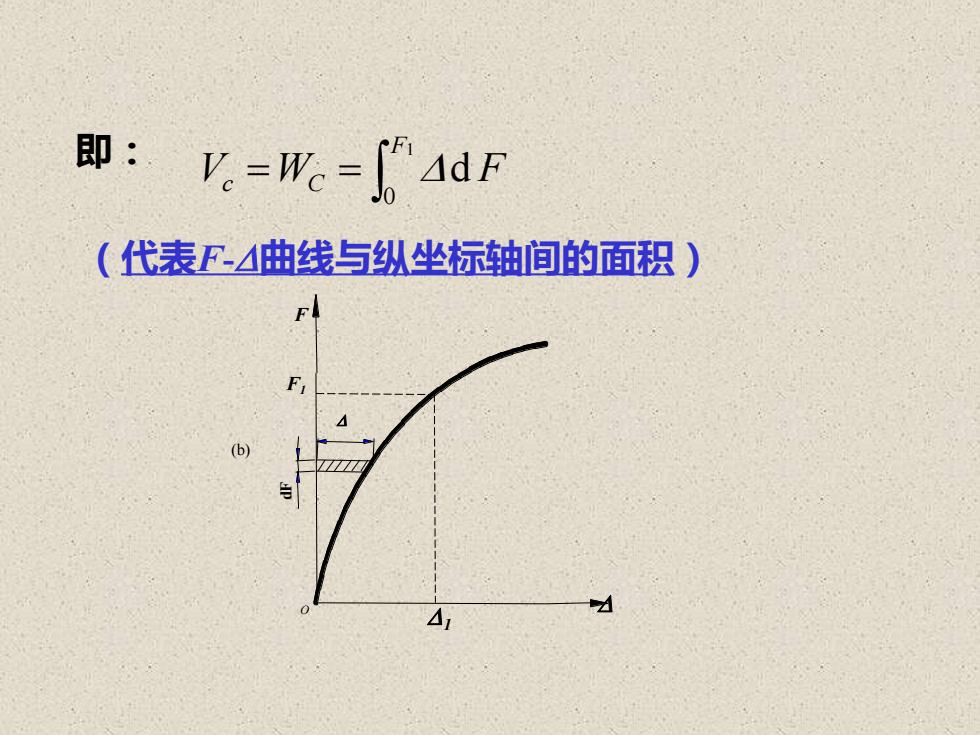
即:V.=Wo-f4dF（代表F-△曲线与纵坐标轴间的面积）b

 = = F Vc WC F 1 0 d （代表F-曲线与纵坐标轴间的面积） 即： F O dF  1 F1  (b)

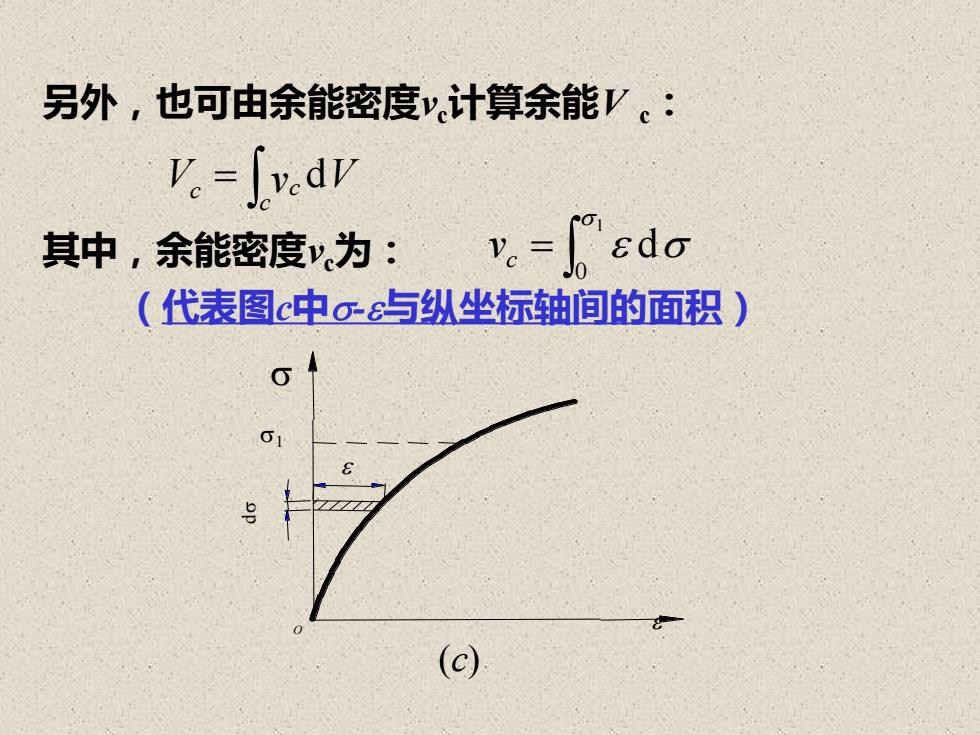
另外，也可由余能密度计算余能V。：V.=J.vedvodoV.=其中，余能密度V为：（代表图c中-&与纵坐标轴间的面积）?S(c)

另外，也可由余能密度vc计算余能V c： V v V c c c d  = 其中，余能密度vc为：  = 1 0 d  vc   （代表图c中-与纵坐标轴间的面积） O d   1  (c) 