内蒙古科技大学：《材料力学》课程PPT教学课件（土木类）第十一章 能量法

注意：对线弹性材料，余能和应变能仅在数值上相等，其概念和计算方法却截然不同。·对非线性材料，则余能V.与应变能V在数值上不一定相等。余功、余能、余能密度都没有具体的物理概念，仅是具有功和能的量纲而已

•对线弹性材料，余能和应变能仅在数值上 相等，其概念和计算方法却截然不同。 注意： •对非线性材料，则余能V c与应变能V 在数值 上不一定相等。 •余功、余能、余能密度都没有具体的物 理概念，仅是具有功和能的量纲而已

例11-3试计算图a所示结构在荷载Fi作用下的余能V。。结构中两杆的长度均为l，横截面面积均为A。材料在单轴拉伸时的应力一应变曲线如图b所示。76g= Ksln (n>1)O(a)(b)aoF81F1解：两杆轴力均为：FN2cosαFiFN两杆横截面上的应力为：01=A2Acosα

例11-3 试计算图a 所示结构在荷载F1作用下的余能 Vc 。结构中两杆的长度均为l，横截面面积均为A。材 料在单轴拉伸时的应力一应变曲线如图b所示。 解： 两杆轴力均为： 2cos F1 F N = 两杆横截面上的应力为：   2 cos 1 1 A F A F N = = O 1 1 (n 1) 1/ =  n  K (b) F1 C B D (a)

由己知6-(0k余能密度为：v。=[eda=(o/)"do所以余能为n+1FiV。= 2 ve(IA) =(2A)" K"(n+1) (cosα

1 1 (2 ) ( 1) cos 2 ( ) +       + =  = n n n c c F A K n l V v lA  所以余能为 余能密度为： ( )   = = 1 1 0 0 d d       n vc K 由已知 ( ) n K  = 

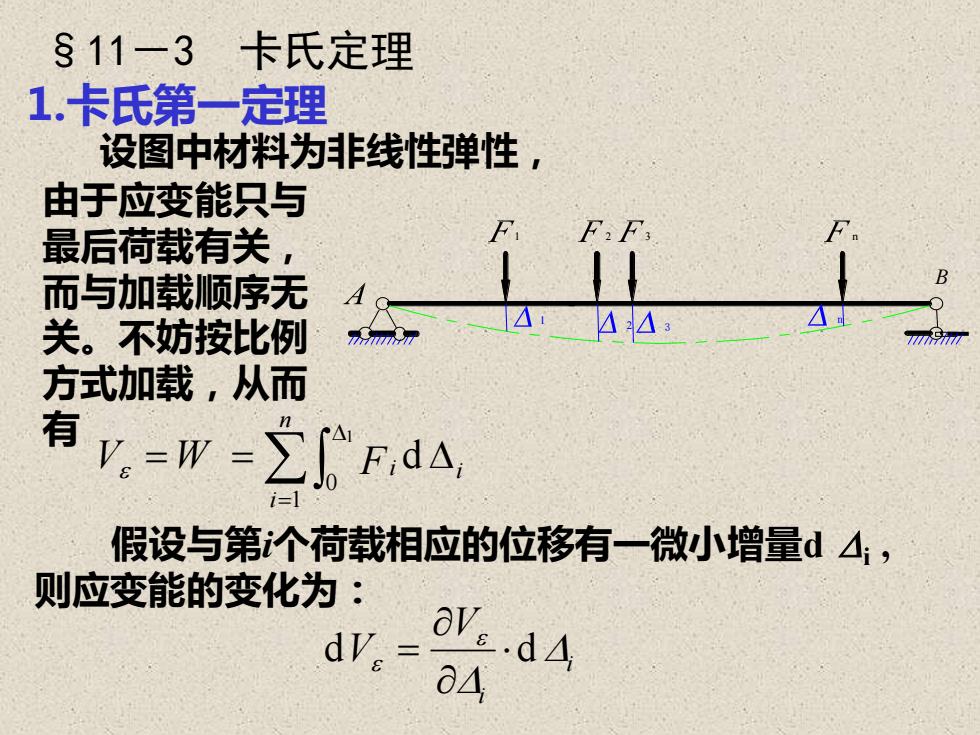
S11-3卡氏定理1.卡氏第一定理设图中材料为非线性弹性，由于应变能只与F.F.F.F最后荷载有关，/B而与加载顺序无41AAN关。不按比例方式加载，从而有V,-w -ZfFida,假设与第i个荷载相应的位移有一微小增量d4;，则应变能的变化为：aV.E.dAdV.4

§11－3 卡氏定理 1.卡氏第一定理 设图中材料为非线性弹性， 由于应变能只与 最后荷载有关， 而与加载顺序无 关。不妨按比例 方式加载，从而 有 i n i V = W =  Fi   =  d 1 0 1  假设与第i个荷载相应的位移有一微小增量d i , 则应变能的变化为： i i V V     d d   = 1 2 3 n 1 2 3 n B

因仅与第个荷载相应的位移有一微小增量，而与其余各荷载相应的位移保持不变，因此，对于位移的微小增量d△：，仅F作了外力功，外力功的变化为：dW=F,d4oV.E.dAdV注意到上式与下式在数值上相等二04av.从而有： F=（卡氏第一定理04注意：·卡氏第一定理既适合于线弹性体，也适合于非线性弹性体。·式中F及4分别为广义力、广义位移。·必须将V.写成给定位移的函数，才可求其变化率

因仅与第i个荷载相应的位移有一微小增量,而与其 余各荷载相应的位移保持不变，因此，对于位移的微 小增量d i ，仅Fi作了外力功，外力功的变化为： dW = Fi di 注意到上式与下式在数值上相等 i i V V     d d   = 从而有： i i V F   =  （卡氏第一定理 ） 注意： •卡氏第一定理既适合于线弹性体，也适合于非线 性弹性体。 •式中Fi及i分别为广义力、广义位移。 •必须将V 写成给定位移的函数，才可求其变化率