内蒙古科技大学：《材料力学》课程PPT教学课件（土木类）第十一章 能量法

若取各边长为单位长的单元体，则作用于上、下F= oxlxl = o表面上的力为：=8x1=8其伸长量为：则作用于此单元体上的外力功为：W-'ode注意到此单元体的体积为单位值，从而此时的应变能（数值上等于上式中的W）为应变能密度：ve=J。ds(α-s曲线与横坐标轴间的面积)

若取各边长为单位长的单元体，则作用于上、下 表面上的力为: F = 11 =  其伸长量为： ＝  1＝  则作用于此单元体上的外力功为：  = 1 0 d  W   注意到此单元体的体积为单位值，从而此时的应 变能(数值上等于上式中的W) 为应变能密度:  = 1 0 d  v   (-曲线与横坐标轴间的面积）  O d  1 1 (c)

若取边长分别为dx、dy、dz的单元体，则此单元体的应变能为：dVe=v.dxdydz整个拉杆的应变能为：V,-fdv,-fvedv（此为由应变能密度计算应变能的表达式）特别地，在拉杆整个体积内为常量所以有V,=VV=V,Al

若取边长分别为dx、dy、dz 的单元体，则此单 元体的应变能为： dV = v d x d y d z 整个拉杆的应变能为： V V v V v v d d    =  =  (此为由应变能密度计算应变能的表达式) 特别地，在拉杆整个体积内vε为常量 V v V v Al 所以有  =  = 

说明：线弹性体的v、V可作为非线性体的v。、V.的特例。由于线弹性的F与4或与成正比，则F-4曲线或。-ε曲线与横坐标轴围成一个三角形，其面积等于应变能V和应变能密度。。EAZ?F?1V.=W-2-Fi△12122EAaiw-ode-o-5ei-22E同理，可得纯剪时的应变能密度为：tive-Jitdy-nn-Gi-2G

说明：线弹性体的v、V 可作为非线性体的v、 V 的 特例。由于线弹性的F与或与 成正比，则F－曲 线或－ 曲线与横坐标轴围成一个三角形，其面积 等于应变能V 和应变能密度v 。 l EA EA F l V W F 2 2 2 1 2 1 2 1 1 1   = =  = = E v E 2 2 1 2 1 d 2 2 1 1 1 1 0 1         = = = =  同理，可得纯剪时的应变能密度v为： G v G 2 2 1 2 1 d 2 2 1 1 1 1 0 1       =   = = = 

例11-1弯曲刚度为E的简支梁受均布荷载g作用，如图所示。试求梁内的应变能。q解：梁的挠曲线方程为：珠）MW-1(ads).w荷载所作外力功为：qrsV.=W--将前一式代入后一式得：240EI

例11-1 弯曲刚度为EI的简支梁受均布荷载q作用， 如图所示。试求梁内的应变能 。 解：梁的挠曲线方程为：         = − + l x l x l x EI ql w 4 4 3 4 3 2 24 荷载所作外力功为： W (q x) w l =   d 2 1 0 将前一式代入后一式得： EI q l V W 240 2 5  = = w x l y A B q x

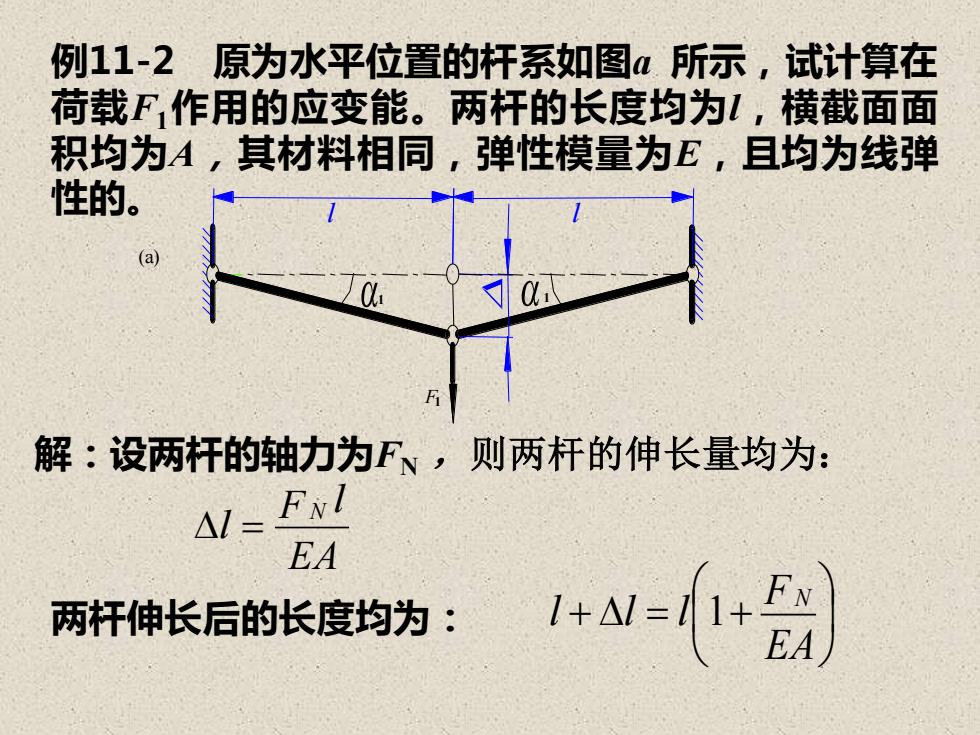
例11-2原为水平位置的杆系如图a所示，试计算在荷载F作用的应变能。两杆的长度均为，横截面面积均为A，其材料相同，弹性模量为E，且均为线弹性的。(a)解：设两杆的轴力为F~，则两杆的伸长量均为：A/=FNIEA1+A/=/1+EN两杆伸长后的长度均为：EA

例11-2 原为水平位置的杆系如图a 所示，试计算在 荷载F1作用的应变能。两杆的长度均为l，横截面面 积均为A，其材料相同，弹性模量为E，且均为线弹 性的。 解：设两杆的轴力为FN ，则两杆的伸长量均为： EA F l l N  = 两杆伸长后的长度均为：       +  = + EA F l l l N 1 F1 1 1 l l (a)