
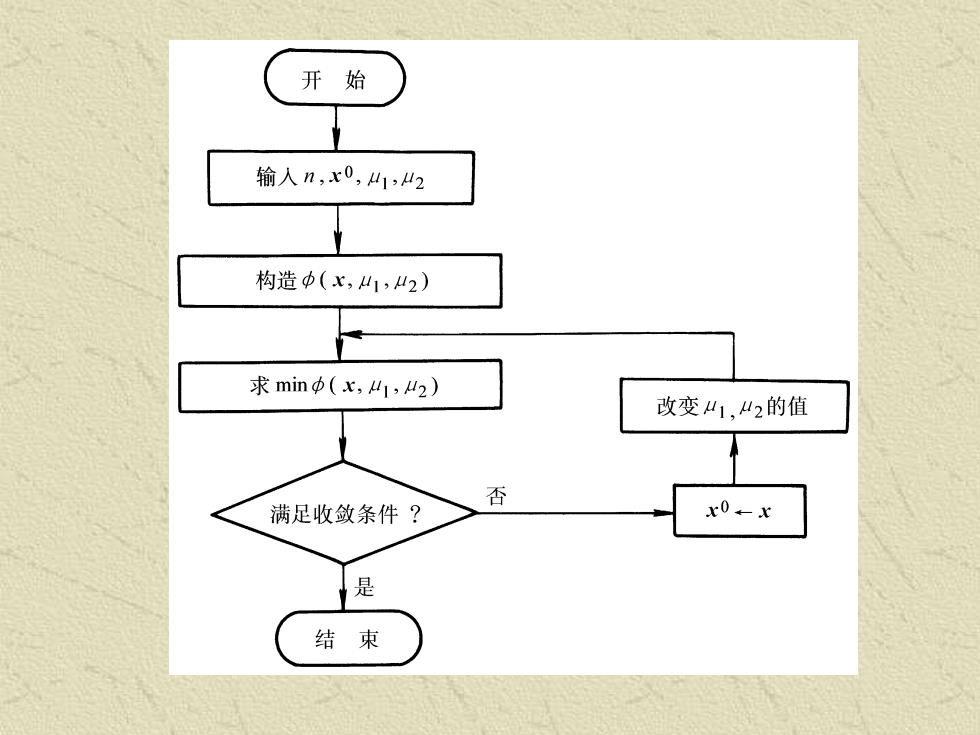
间接解法的求解思路: 将约束函数进行特殊的加权处理后,和目标函数结合起来, 构成一个新的目标函数,即将原约束优化问题转化为一个 或一系列的无约束优化问题。 ( 1 2 1 2 ) ( ) ( ) ( ) 1 1 , , m l j k j k x f x G g x H h x = = = + + 新目标函数 加权因子 然后对新目标函数进行无约束极小化计算
间接解法的求解思路: 将约束函数进行特殊的加权处理后,和目标函数结合起来, 构成一个新的目标函数,即将原约束优化问题转化为一个 或一系列的无约束优化问题。 ( 1 2 1 2 ) ( ) ( ) ( ) 1 1 , , m l j k j k x f x G g x H h x = = = + + 新目标函数 加权因子 然后对新目标函数进行无约束极小化计算
开始 输人n,x0,41,2 构造中(x,山1,2) 求min中(x,41,42) 改变41,42的值 否 满足收敛条件? x0←x 是 结束

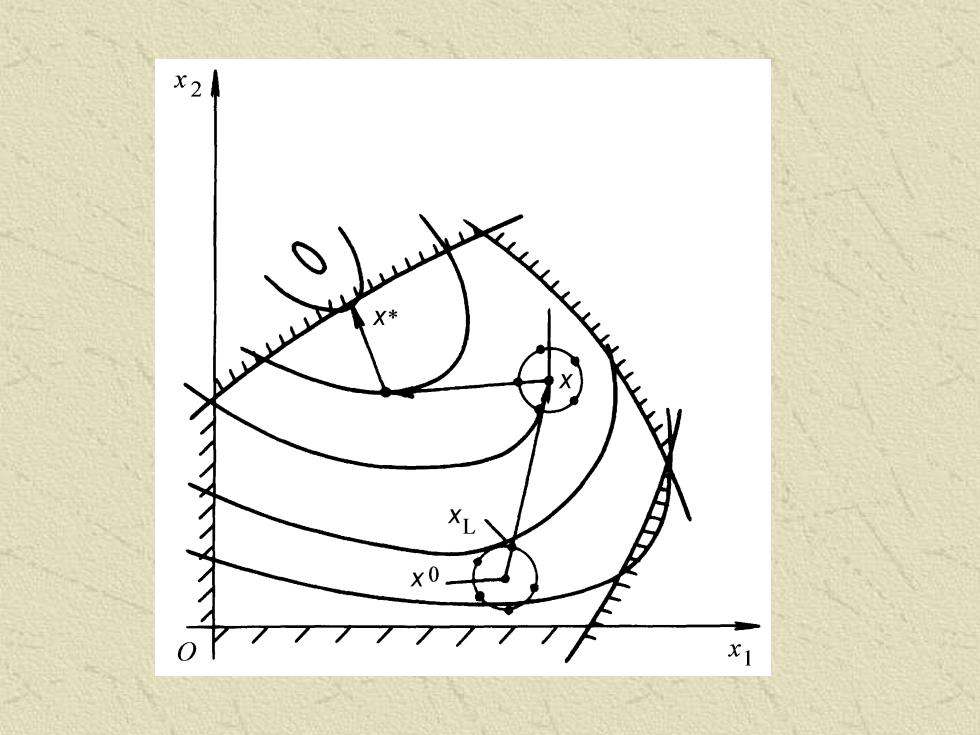
第二节随机方向法 随机方向法的基本思路: 在可行域内选择一个初始点,利用随机数的概率特性,产 生若干个随机方向,并从中选择一个能使目标函数值下降 最快的随机方向作为搜索方向d。 从初始点x0出发,沿d 方向以一定步长进行搜索,得到新点 X,新点x应满足约束条件且f(x)<f(x0),至此完成一次迭代。 基本思路如图所示。 随机方向法程序设计简单,搜索速度快,是解决小型机械优 化问题的十分有效的算法
第二节随机方向法 随机方向法的基本思路: 在可行域内选择一个初始点,利用随机数的概率特性,产 生若干个随机方向,并从中选择一个能使目标函数值下降 最快的随机方向作为搜索方向d。 从初始点x0出发,沿d 方向以一定步长进行搜索,得到新点 X,新点x应满足约束条件且f(x)<f(x0),至此完成一次迭代。 基本思路如图所示。 随机方向法程序设计简单,搜索速度快,是解决小型机械优 化问题的十分有效的算法
×2 X 0

一、随机数的产生 下面介绍一种常用的产生随机数的数学模型 35 36 37 1 2 3 首先令 r r r = = = 2 , 2 , 2 取r=2657863,按一下步 骤计算: 令 r r 5 若 3 r r 则 3 r r r − 若 则 2 r r r − 2 r r 1 若 r r 1 则 r r r − 则 1 q r r = / (0,1)之间的随机数
一、随机数的产生 下面介绍一种常用的产生随机数的数学模型 35 36 37 1 2 3 首先令 r r r = = = 2 , 2 , 2 取r=2657863,按一下步 骤计算: 令 r r 5 若 3 r r 则 3 r r r − 若 则 2 r r r − 2 r r 1 若 r r 1 则 r r r − 则 1 q r r = / (0,1)之间的随机数