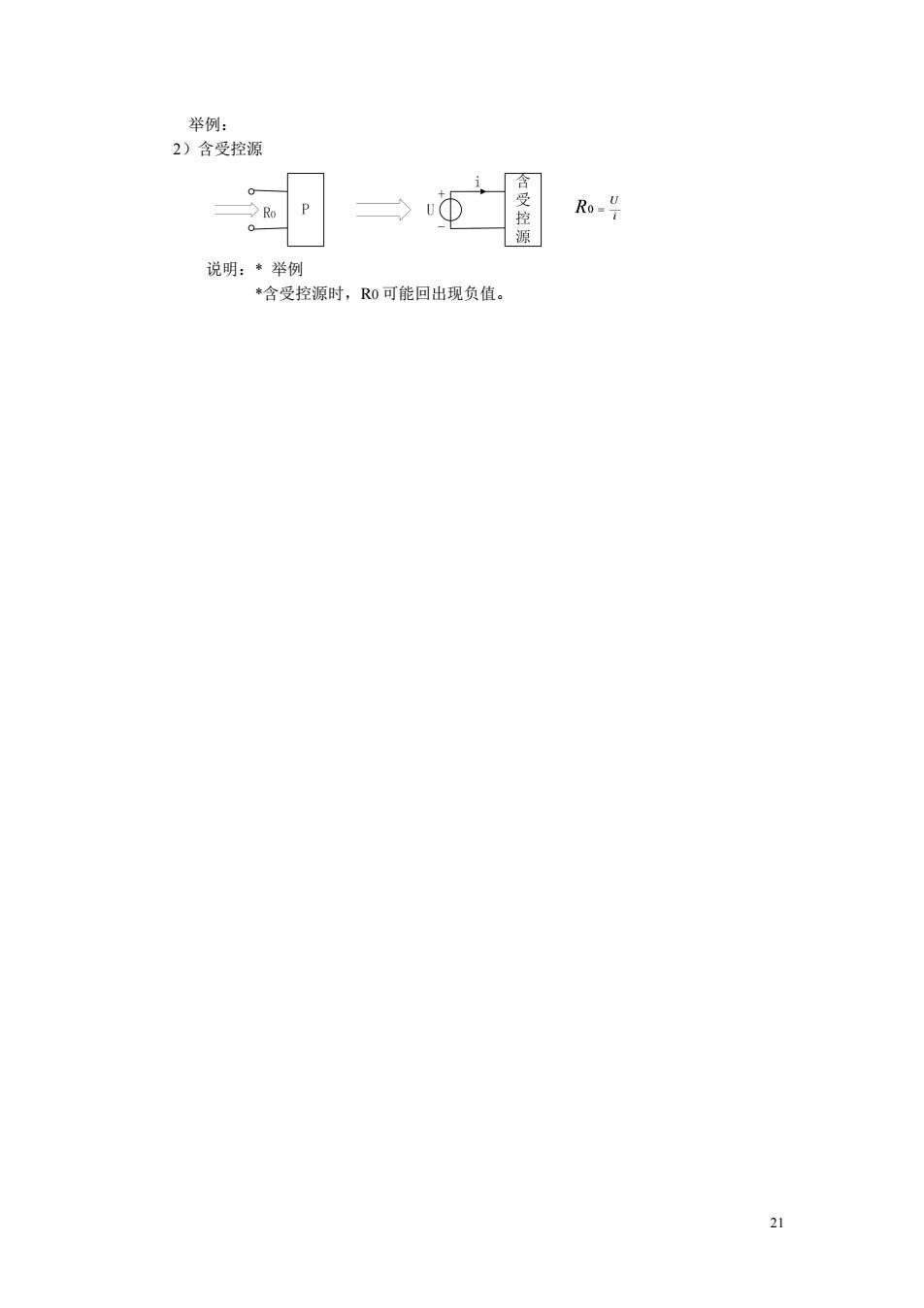
举例: 2)含受控源 Ro 含受控 Ro-4 说明:*举例 *含受控源时,R0可能回出现负值。 21
21 举例: 2)含受控源 说明:* 举例 *含受控源时,R0 可能回出现负值
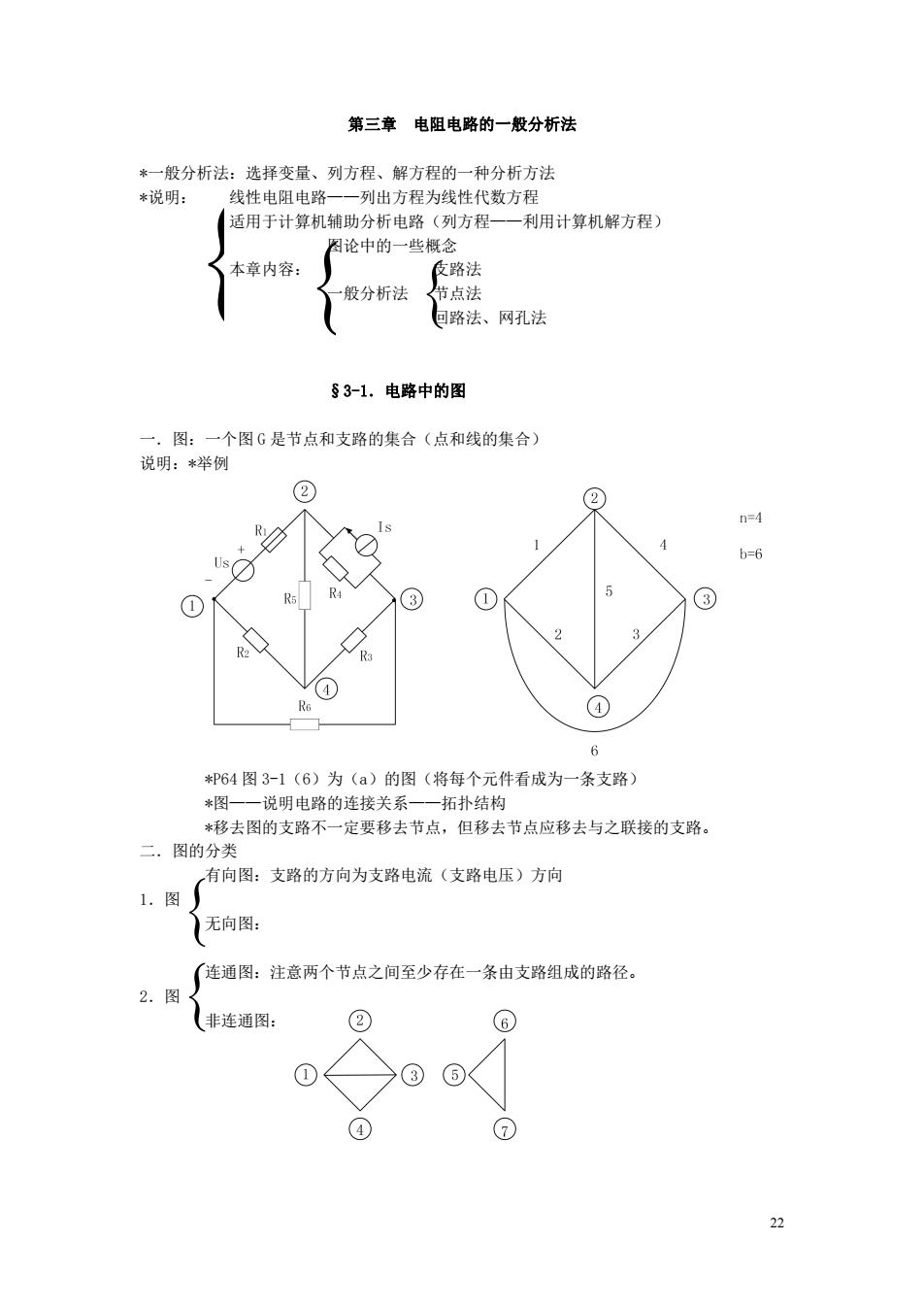
第三章电阻电路的一般分析法 *一般分析法:选择变量、列方程、解方程的一种分析方法 *说明: 线性电阻电路一一列出方程为线性代数方程 适用于计算机辅助分析电路(列方程一一利用计算机解方程) 图论中的一些概念 本章内容: 及路法 般分析法 节点法 回路法、网孔法 §3-1.电路中的图 一,图:一个图G是节点和支路的集合(点和线的集合) 说明:*举例 ② (2 n=4 R 4 b=6 R4 ① ① 5 ③ R2 R3 4 (4 6 P64图3-1(6)为(a)的图(将每个元件看成为一条支路) *图一一说明电路的连接关系一一拓扑结构 *移去图的支路不一定要移去节点,但移去节点应移去与之联接的支路。 二.图的分类 有向图:支路的方向为支路电流(支路电压)方向 1.图 无向图: (连通图:注意两个节点之间至少存在一条由支路组成的路径。 2.图 非连通图: ② 6 1 3 5 ④ ⑦ 22
22 第三章 电阻电路的一般分析法 *一般分析法:选择变量、列方程、解方程的一种分析方法 *说明: 线性电阻电路——列出方程为线性代数方程 适用于计算机辅助分析电路(列方程——利用计算机解方程) 图论中的一些概念 本章内容: 支路法 一般分析法 节点法 回路法、网孔法 §3-1.电路中的图 一.图:一个图 G 是节点和支路的集合(点和线的集合) 说明:*举例 *P64 图 3-1(6)为(a)的图(将每个元件看成为一条支路) *图——说明电路的连接关系——拓扑结构 *移去图的支路不一定要移去节点,但移去节点应移去与之联接的支路。 二.图的分类 有向图:支路的方向为支路电流(支路电压)方向 1.图 无向图: 连通图:注意两个节点之间至少存在一条由支路组成的路径。 2.图 非连通图:

平面图:各支路不交叉(所有节点和支路在一个平面上) 3.图 (非平面图:各支路间出现交叉 三.概念 1.回路:图中任一闭合路径。 2.网孔:内部不含支路的回路。 3.子图:一个图的子图T:子图T的所有支路,节点均属于G。 4.路径:从图G某点出发沿着一些支路连续移动,从而到达另一个节点,这些支路构成图 G的一条路径。 §3-2KCL、KVL的独立方程数 一.树 连通图G的一个树T是指G的一个连通子图 连通 含有G的全部节点 但不含回路 说明:*举例 (树支:组成树的支路 (n-1)个树支 *树 连支:不属于树的支路 b-(n-1)个连支 *树支数为n-1证明 n个节点一一>先用一支路连接两节点一一>每加一个支路联一个新节点一一>n个节 点全部连接需要n-1个支路 二.单连支回路(基本回路) 1.单连支回路:对于任选一个树每加一个连支构成一个回路 说明:*举例 *树选择不同,基本回路也不同 2.基本回路特点:每一个基本回路均有一个其它回路没有的新连支(基本回路是独立的) 3.基本回路的个数:b-(n-1) 4.网孔(平面电路)一一为基本回路的特例 三.KCL、KVL独立方程数 1.KCL独立方程数 (1)KCL独立性(举例分析) 例: A KCL:+1-13=0 21 13 B KCL:-I1-I2+I3=0 R3 2个KCL只有一个独立的KCL Us2 23
23 平面图:各支路不交叉(所有节点和支路在一个平面上) 3.图 非平面图:各支路间出现交叉 三.概念 1.回路:图中任一闭合路径。 2.网孔:内部不含支路的回路。 3.子图:一个图的子图 T:子图 T 的所有支路,节点均属于 G。 4.路径:从图 G 某点出发沿着一些支路连续移动,从而到达另一个节点,这些支路构成图 G 的一条路径。 §3-2 KCL、KVL 的独立方程数 一.树 连通图 G 的一个树 T 是指 G 的一个连通子图 连通 含有 G 的全部节点 但不含回路 说明:*举例 树支:组成树的支路 (n-1)个树支 *树 连支:不属于树的支路 b-(n-1)个连支 *树支数为 n-1 证明 n 个节点——>先用一支路连接两节点——>每加一个支路联一个新节点——>n 个节 点全部连接需要 n-1 个支路 二.单连支回路(基本回路) 1. 单连支回路:对于任选一个树每加一个连支构成一个回路 说明:*举例 *树选择不同,基本回路也不同 2.基本回路特点:每一个基本回路均有一个其它回路没有的新连支(基本回路是独立的) 3.基本回路的个数:b-(n-1) 4.网孔(平面电路)——为基本回路的特例 三.KCL、KVL 独立方程数 1. KCL 独立方程数 (1) KCL 独立性(举例分析) 例 : A KCL: 1 2 3 I I I 0 B KCL: 1 2 3 I I I 0 2 个 KCL 只有一个独立的 KCL
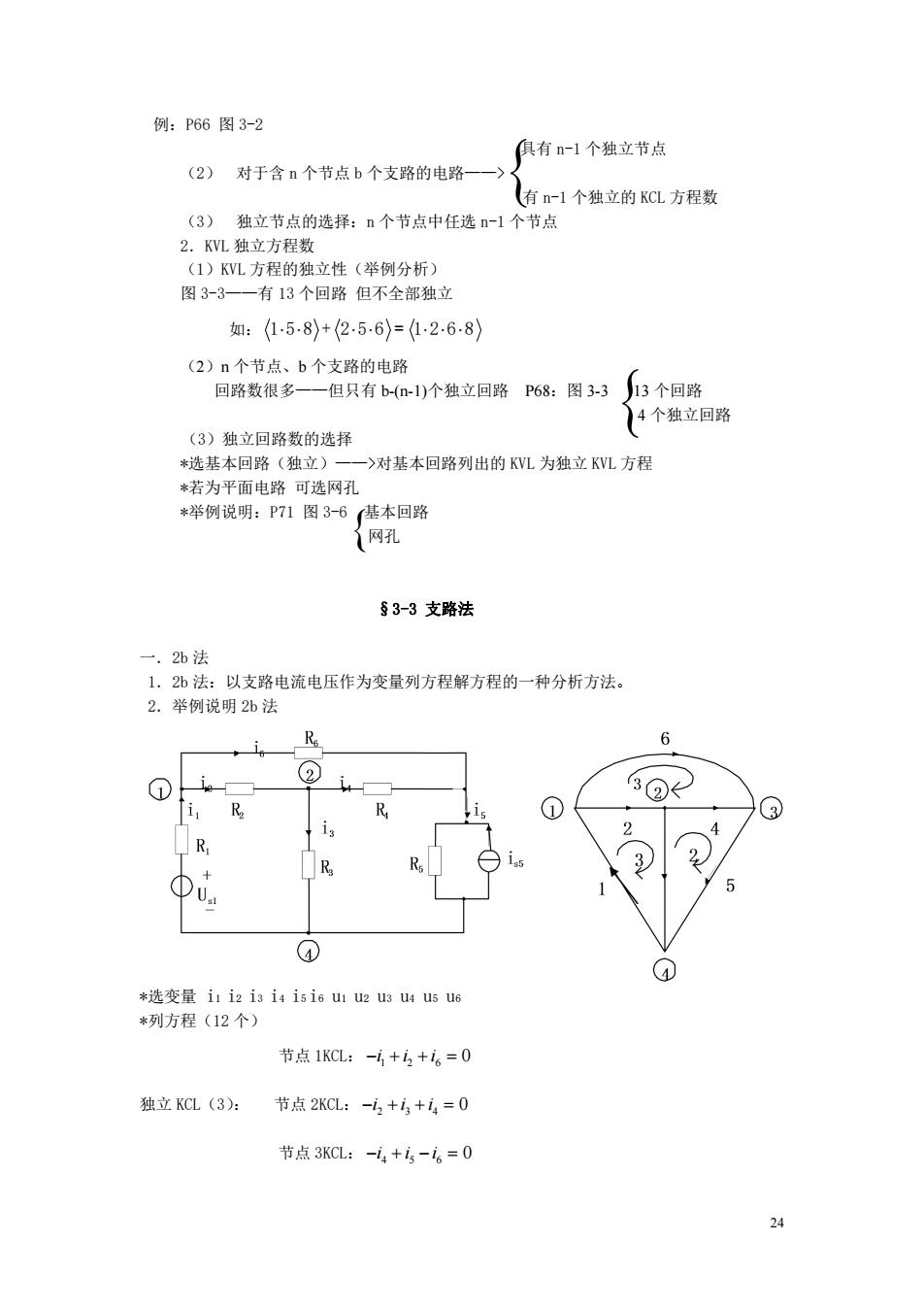
例:P66图3-2 俱有n-1个独立节点 (2)对于含n个节点b个支路的电路 有n-1个独立的KCL方程数 (3)独立节点的选择:n个节点中任选n-1个节点 2.KVL独立方程数 (1)KVL方程的独立性(举例分析) 图3-3一一有13个回路但不全部独立 如:15.8)+(25.6)=126.8》 (2)n个节点、b个支路的电路 回路数很多一一但只有b-(n-1)个独立回路 P68:图3-3 3个回路 (4个独立回路 (3)独立回路数的选择 *选基本回路(独立)一一>对基本回路列出的KVL为独立KVL方程 *若为平面电路可选网孔 *举例说明:P71图3-6基本回路 网孔 §3-3支路法 一.2b法 1.b法:以支路电流电压作为变量列方程解方程的一种分析方法。 2.举例说明2弘法 R 6 2 3②K 3 2 R 3 + 5 ④ *选变量i1i2i3i4i5i6u1u2u3u4u5u6 *列方程(12个) 节点1KCL:-4+2+i6=0 独立KCL(3): 节点2KCL:-2+43+i4=0 节点3KCL:-14+i-6=0 24
24 例:P66 图 3-2 具有 n-1 个独立节点 (2) 对于含 n 个节点 b 个支路的电路——> 有 n-1 个独立的 KCL 方程数 (3) 独立节点的选择:n 个节点中任选 n-1 个节点 2.KVL 独立方程数 (1)KVL 方程的独立性(举例分析) 图 3-3——有 13 个回路 但不全部独立 如: 158 + 256 = 1268 (2)n 个节点、b 个支路的电路 回路数很多——但只有 b-(n-1)个独立回路 P68:图 3-3 13 个回路 4 个独立回路 (3)独立回路数的选择 *选基本回路(独立)——>对基本回路列出的 KVL 为独立 KVL 方程 *若为平面电路 可选网孔 *举例说明:P71 图 3-6 基本回路 网孔 §3-3 支路法 一.2b 法 1.2b 法:以支路电流电压作为变量列方程解方程的一种分析方法。 2.举例说明 2b 法 *选变量 i1 i2 i3 i4 i5 i6 u1 u2 u3 u4 u5 u6 *列方程(12 个) 节点 1KCL: 1 2 6 i i i 0 独立 KCL(3): 节点 2KCL: 2 3 4 i i i 0 节点 3KCL: 4 5 6 i i i 0

网孔1:4+山2+4=0 独立KVL(3)(网孔): 网孔2:-43+44+4=0 网孔3:-山2-44+46=0 支路VAR(6): 4=-41+R 44=R4i4 h2=R52 43=R3 46=R6 *解方程求出i1~i6u1~u6 3.对于含n个节点b个支路的电路2b法需列2b个方程 n-1个KCL 2b个方程: b-(n-1)KVL b个支路VAR 4.说明:*支路方程的列写 *含可控源支路方程列写:与独立源相同 R VAR:u=Ri Us VAR:u=Us+Ri × 1 RU VAR:i-i,-U 十 VAR:U=Us VAR i=is 25
25 网孔 1: 1 2 3 u u u 0 独立 KVL(3)(网孔): 网孔 2 : 3 4 5 u u u 0 网孔 3: 2 4 6 u u u 0 支路 VAR(6): *解方程求出 i1 ~ i6 u1 ~ u6 3.对于含 n 个节点 b 个支路的电路 2b 法需列 2b 个方程 n-1 个 KCL 2b 个方程: b-(n-1)KVL b 个支路 VAR 4.说明:*支路方程的列写 *含可控源支路方程列写:与独立源相同 VAR:u = Ri S VAR:u = U + Ri s U VAR:i = i - R S VAR:U = U VAR:i = is 1 1 1 1 2 2 2 3 3 3 s u u R i u R i u R i 4 4 4 5 5 5 5 6 6 6 s u R i u i i R u R i