《高等数学》课程教学资源（PPT课件）第十章 重积分_第四节 二重积分习题课_二重积分习题课

二重积分习题课 一、内容提要 二、 题型练习

二重积分习题课 一、内容提要 二、题型练习

题型练习 (一) 利用对称性简化计算 (二) 选择坐标系和积分次序 (三)交换积分次序 (四) 绝对值拯数的二重积分 (五)证明题

二、题型练习 （一）利用对称性简化计算 （二）选择坐标系和积分次序 （三）交换积分次序 （四）绝对值函数的二重积分 （五）证明题

二、题型练习 (一）利用对称性简化计算 (二) 选择坐标系和积分次序 (三) 交换积分次序 (四) 绝对值函数的二重积分 (五)证明题

二、题型练习 （一）利用对称性简化计算 （二）选择坐标系和积分次序 （三）交换积分次序 （四）绝对值函数的二重积分 （五）证明题

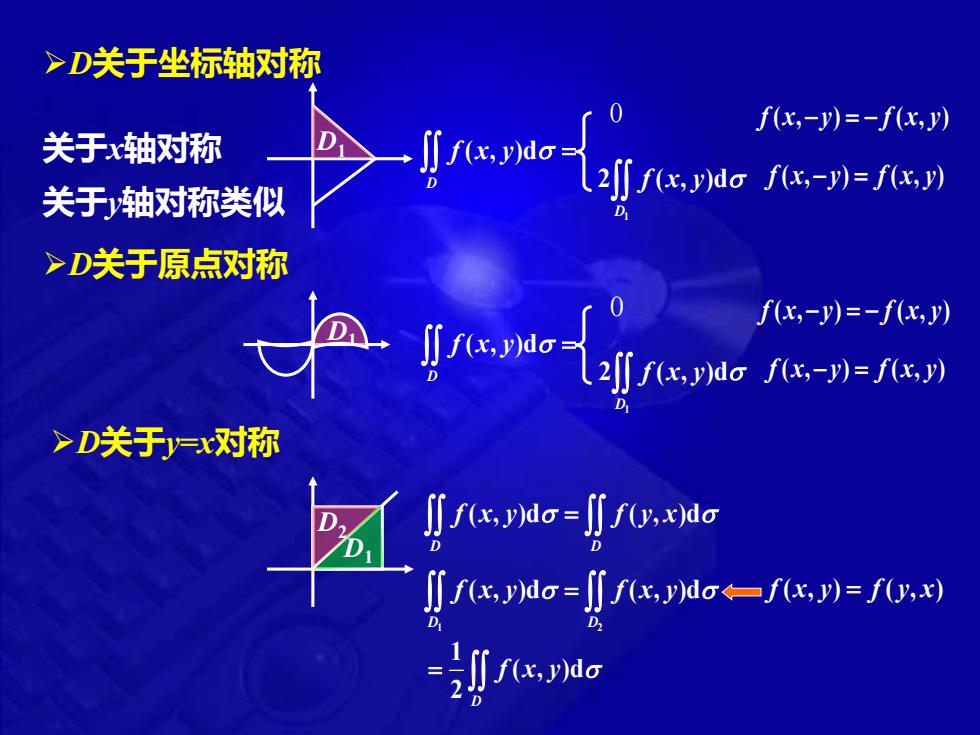
>D关于坐标轴对称 f化，-)=-f(化，) 关于x轴对称 关于轴对称类似 >D关于原点对称 f(x,-y)=-f(x,) >D关于=x对称 ∬ao-ac ∬fx,ao=∬fc,aG-fx,)=0

➢D关于坐标轴对称 关于x轴对称 D1 ( , )d D f x y  =  1 2 ( , )d D f x y   f x y f x y ( , ) ( , ) − = 0 f x y f x y ( , ) ( , ) − = − 关于y轴对称类似 ➢D关于原点对称 D1 ➢D关于y=x对称 D2 D1 ( , )d ( , )d D D f x y f y x   =   1 2 ( , )d ( , )d D D f x y f x y   =   f x y f y x ( , ) ( , ) = 1 ( , )d 2 D = f x y  ( , )d D f x y  =  1 2 ( , )d D f x y   f x y f x y ( , ) ( , ) − = 0 f x y f x y ( , ) ( , ) − = −

◆例1设区域D:-1≤x≤1，-2≤y≤2；D2:0≤x≤1,0≤y≤2 =+)广o,=+yo,4和，有何联系？ ◆例2设区域D由y=V1-x,y=0围成，D是D在第一象限的部分， ∬2+3gag=_ ◆例3设区域D由y=sinx,y=0,-π≤x≤π围成， D是D在第一象限的部分，(x+)sin()do= ◆例4设区域D由x+y≤1围成，D,是D在第一象限的部分， J∬x-yao=

◆例1 ◆例2 设区域D由 2 y x y = − = 1 , 0 围成, D1是D在第一象限的部分, 2 2 ( 3 )d _ D x xy + =   ◆例3 ◆例4 设区域D由 x y +  1 围成, D1是D在第一象限的部分, ( )d _ n n D x y − =   设区域 1 2 2 2 2 2 1 2 ( )d , ( )d , D D I f x y I f x y = + = +     I1 和I2有何关系? 1 2 D x y D x y : 1 1, 2 2; : 0 1,0 2; −   −       设区域D由 y x y x = = −   sin , 0,   围成, ( )sin( )d _ D x y xy + =  D1是D在第一象限的部分, 