
具有隐含状态机制的RNN ·输入向量序列X1…,X7 ·隐含状态向量序列 。h1,,h7 ·ht=f(ht-1xt) ·输出向量 ·序列01,0r;0t=g(ht) ·读取序列以生成隐含状态,然后开始生成输出 ·输出向量通常用作下一个隐含状态的输入 D2L.ai
具有隐含状态机制的RNN • 输入向量序列 �$, … , �+ • 隐含状态向量序列 • �$, … , �+ • �! = �(�!#$, �!) • 输出向量 • 序列 �$, … , �+; �! = �(�!) • 读取序列以生成隐含状态,然后开始生成输出 • 输出向量通常用作下一个隐含状态的输入
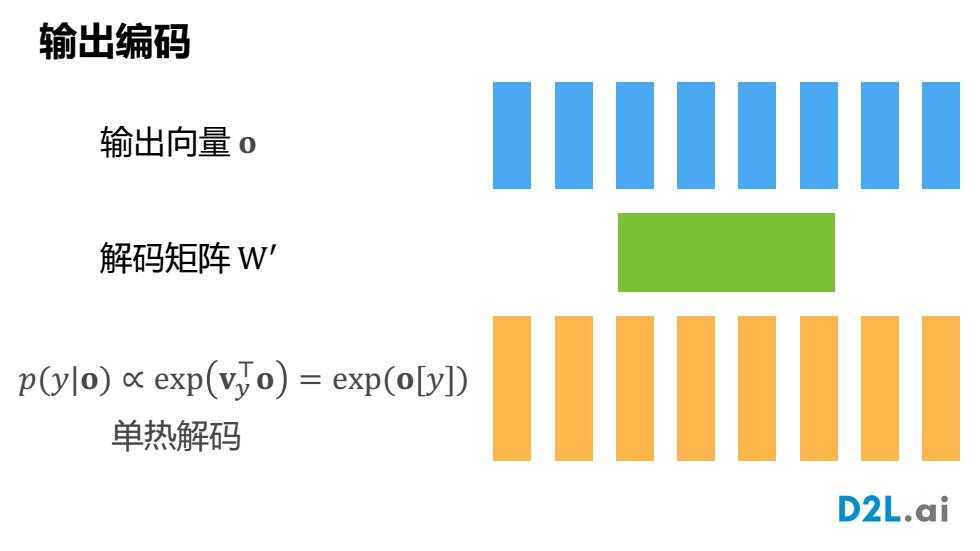
输出编码 输出向量0 解码矩阵W' p(ylo)x exp(vyo)=exp(o[y]) 单热解码 D2L.ai
输出编码 解码矩阵 W, 输出向量 � �(�|�) ∝ exp �- .� = exp(�[�]) 单热解码

梯度 ·反向传播的长链依赖关系 ·需要在内存中保留很多中间值 ·蝴蝶效应 ·梯度消失或发散(稍后会详细介绍) ·裁剪梯度以防止发散 gmin(,g ·重新缩放到最大尺寸为0的梯度 D2L.ai
梯度 • 反向传播的长链依赖关系 • 需要在内存中保留很多中间值 • 蝴蝶效应 • 梯度消失或发散(稍后会详细介绍) • 裁剪梯度以防止发散 • 重新缩放到最大尺寸为 � 的梯度 � ← min 1, � ∥ � ∥ �

困惑度 ·通常使用对数似然来测量准确度 ·这使得不同长度的输出无法比较 (例如,一个坏模型的较短输出的效果可能比一个优秀模 型的较长输出的性能具有更好的对数似然) ·将对数似然标准化为序列长度 T Σlogp(y:Imodel) VS. π:=- t=1 lo(y:model) ·困惑度是指数版本exp(π) (平均有效选择的数量) D2L.ai
困惑度 • 通常使用对数似然来测量准确度 • 这使得不同长度的输出无法比较 (例如,一个坏模型的较短输出的效果可能比一个优秀模 型的较长输出的性能具有更好的对数似然) • 将对数似然标准化为序列长度 • 困惑度是指数版本 exp(�) (平均有效选择的数量) − ∑ !/$ + log�(�!|model) vs. �: = − 1 � ∑ !/$ + log�(�!|model)
代码.… D2L.ai
代码 …