
When gradient is small .. Hung-yi Lee李宏毅
When gradient is small … Hung-yi Lee 李宏毅
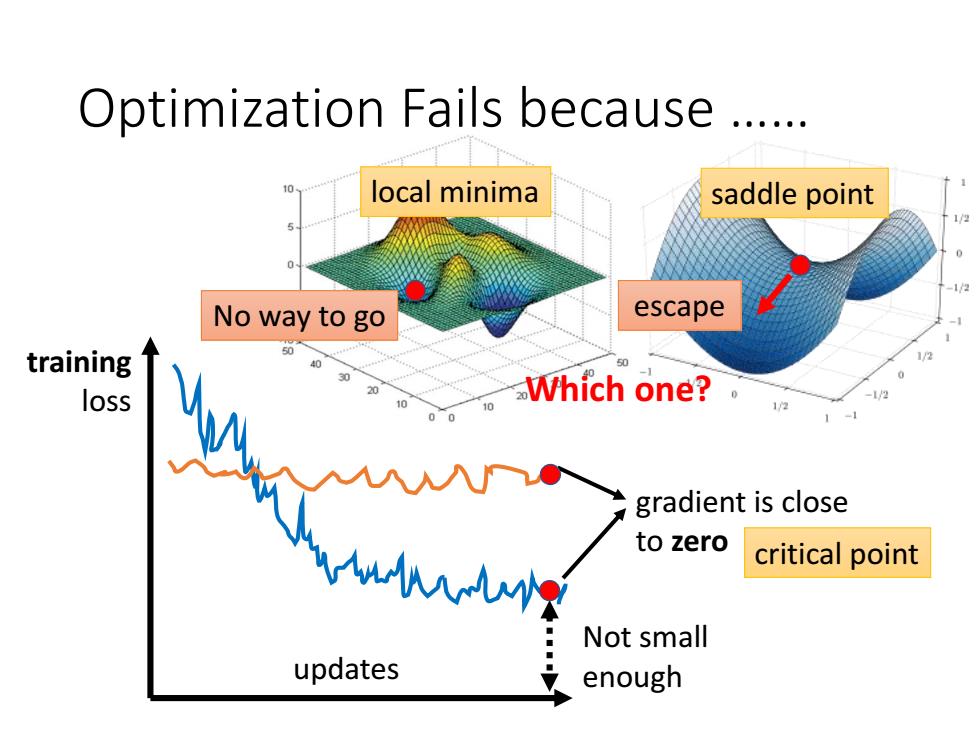
Optimization Fails because ..... local minima saddle point No way to go escape training 40 50 loss 00 0 Which one?。 1/2 gradient is close to zero critical point Not small updates enough
local minima Optimization Fails because …… updates training loss Not small enough gradient is close to zero saddle point critical point Which one? No way to go escape

Warning of Math
Warning of Math

Tayler Series Approximation L(g)aroundθ=θ'can be approximated below L(0)≈L(a)+0-8)rg+E(0-g)H(g-g) Gradient g is a vector aL(0) g=7L(0) gi=001 L(0) Hessian H is a matrix 02 Hi=0010 、L(0')
Tayler Series Approximation 𝐿 𝜽 ≈ 𝐿 𝜽 ′ + 𝜽 − 𝜽 ′ 𝑇𝒈 + 1 2 𝜽 − 𝜽 ′ 𝑇𝐻 𝜽 − 𝜽 ′ Gradient 𝒈 is a vector Hessian 𝐻 is a matrix 𝒈𝑖 = 𝜕𝐿 𝜽 ′ 𝜕𝜽𝑖 𝐻𝑖𝑗 = 𝜕 2 𝜕𝜽𝑖𝜕𝜽𝑗 𝐿 𝜽 ′ 𝒈 = 𝛻𝐿 𝜽 ′ 𝐿 𝜽 around 𝜽 = 𝜽 ′ can be approximated below 𝜽 ′ 𝜽 𝐿 𝜽
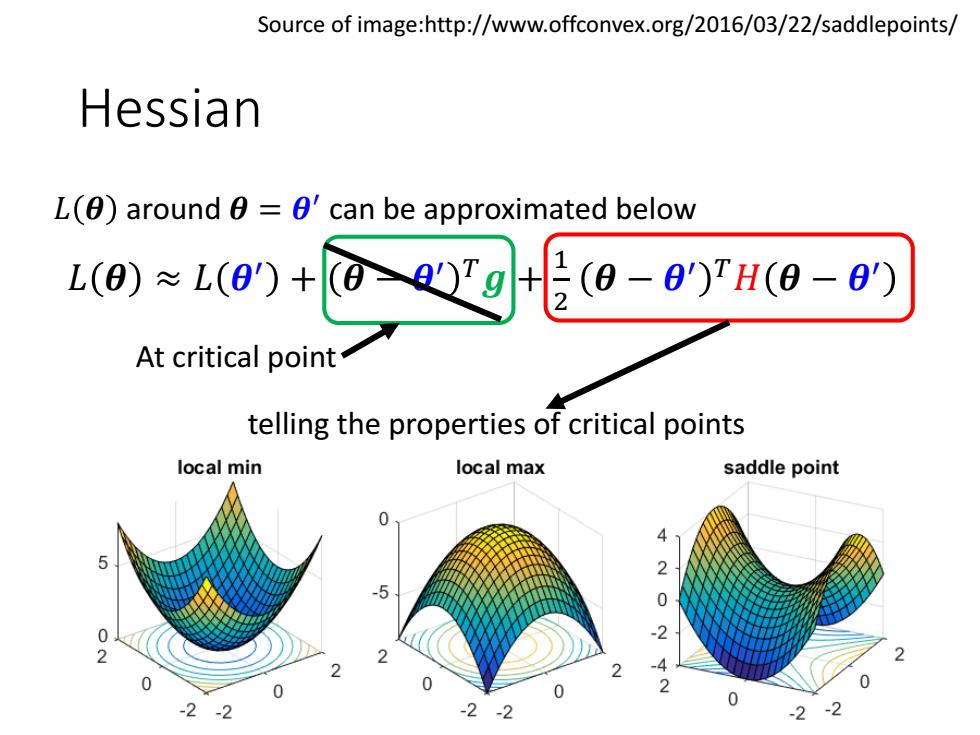
Source of image:http://www.offconvex.org/2016/03/22/saddlepoints/ Hessian L()around =0'can be approximated below L(0)*1(9)+00☑叶60-9H6-0y At critical point telling the properties of critical points local min local max saddle point 4 2 0 0 0 -2-2 -2-2 -2
Hessian Source of image:http://www.offconvex.org/2016/03/22/saddlepoints/ telling the properties of critical points 𝐿 𝜽 ≈ 𝐿 𝜽 ′ + 𝜽 − 𝜽 ′ 𝑇𝒈 + 1 2 𝜽 − 𝜽 ′ 𝑇𝐻 𝜽 − 𝜽 ′ 𝐿 𝜽 around 𝜽 = 𝜽 ′ can be approximated below At critical point