西安电子科技大学：《数字信号处理》课程教学课件（讲稿）03 离散傅里叶变换DFT及其快速算法FFT

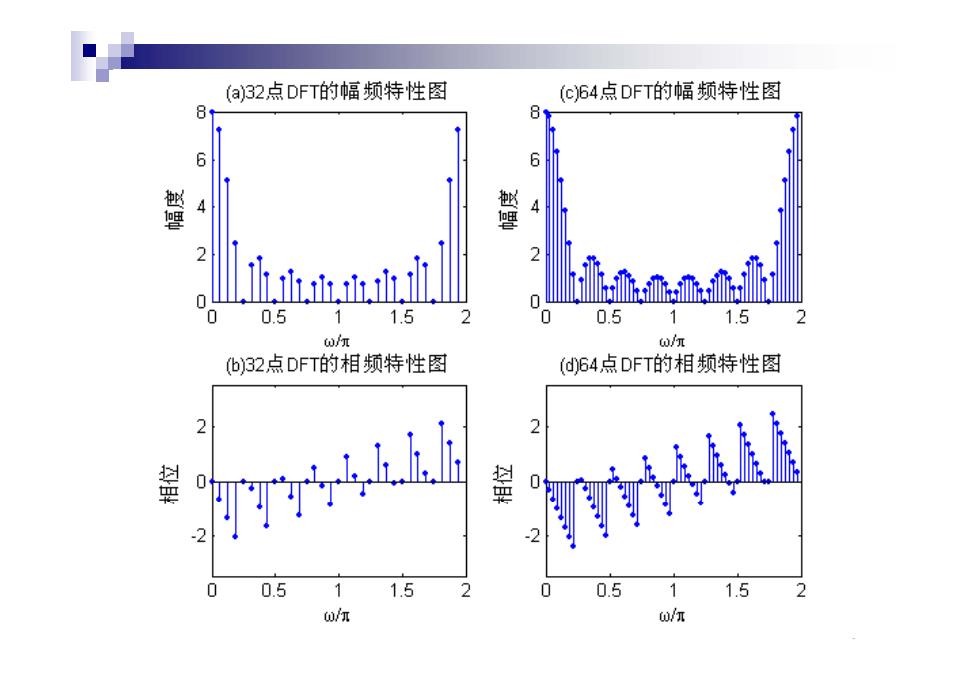
3.1.4用MATLAB计算序列的DFT ■xn=[11111111];%输入时域序列向量xn=R8() ■Xk32=fft(xn,32; %计算xn的32点DFT ■ Xk64=t(xn,64): %计算xn的64点DFT ■ %以下为绘图部分 ■k=0:31;wk=2*k/32; %产生32点DFT对应的采样点频率（关于π归一化值） ■subplot(2,2,1);stem(wk,abs(Xk32),'.)；%绘制32点DFT的幅频特性图 tite('(a)32点DFT的幅频特性图)；xlabel(('wApi);ylabel(幅度) subplot(2,2,3);stem(wk,angle(Xk32),');%绘制32点DFT的相频特性图 title((b)32点DFT的相频特性图)； xlabel('wpi')ylabel('相位)；axis(0,2,-3.5,3.5]) k=0:63;wk=2*k/64;%产生64点DFT对应的采样点频率（关于π归一化值） subplot(2,2,2);stem(wk,abs(Xk64),');%绘制64点DFT的幅频特性图 title(c)64点DFT的幅频特性图)；xlabel('wpi门ylabel(幅度) subplot(2,2,4);stem(wk,angle(Xk64),'.);%绘制64点DFT的相频特性图 title('(d)64点DFT的相频特性图) xlabel('w/pi)ylabel('相位')；axis(0,2,-3.5,3.5]) 24

3.1.4用MATLAB计算序列的DFT  xn=[1 1 1 1 1 1 1 1]; %输入时域序列向量xn=R8(n)  Xk32=fft( ) xn,32 ; %计算xn的32点DFT  Xk64=fft(xn,64); %计算xn的64点DFT  %以下为绘图部分  k=0:31;wk=2*k/32; % k=0:31;wk=2*k/32; %产生32点DFT对应的采样点频率 对应的采样点频率(关于π归一化值)  subplot(2,2,1);stem(wk,abs(Xk32),'.'); %绘制32点DFT的幅频特性图  title('(a)32点DFT的幅频特性图');xlabel('ω/\pi');ylabel('幅度')  subplot(2,2,3);stem(wk,angle(Xk32),'.'); %绘制32点DFT的相频特性图  title('(b)32点DFT的相频特性图');  xlabel( xlabel('ω/\pi );ylabel( ');ylabel('相位');axis([0,2, );axis([0,2,-3.5,3.5]) 3.5,3.5])  k=0:63;wk=2*k/64; %产生64点DFT对应的采样点频率(关于π归一化值)  subplot(2,2,2);stem(wk,abs(Xk64),'.'); %绘制64点DFT的幅频特性图  titl ('( )64 title('(c)64点DFT的幅频特性图') l b l(' ');xlabel('ω/\pi') l b l(' i');ylabel('幅度')  subplot(2,2,4);stem(wk,angle(Xk64),'.'); %绘制64点DFT的相频特性图  title('(d)64点DFT的相频特性图') 24 (( )  xlabel('ω/\pi');ylabel('相位');axis([0,2,-3.5,3.5])

(a)32点DFT的幅频特性图 (c64点DFT的幅频特性图 8 6 6 越 譬 2 .h 色亚 0.5 1 1.5 0 0.5 1.5 红 w/π b)32点DFT的相频特性图 (d64点DFT的相频特性图 0.5 1.5 0.5 1.5 0/T w/n

25

小结 ■DFT引入的目的 ■DFT的定义 ■DFT与DFS、ZT、FT之间的关系 ■DFT、IDFT的计算 ■DFT的矩阵表示 26

小结  DFT 引入的目的  DFT 的定义  DFT与DFS、ZT、FT之间的关系  DFT、IDFT的计算  DFT的矩阵表示 26

3.2离散傅里叶变换(DFT) 的主要性质

3 2. 离散傅里叶变换 离散傅里叶变换（DFT） 的主要性质

1.线性性质 ■设x(n),x2(n)为有限长序列，长度分别为NN2 ■它们的离散傅里叶变换分别为 X (k)=DFT[x (n)] X2 (k)=DFT[x2 (n)]y N2 max[N,N2] ■若 x(n)=ax (n)+bx,(n) ■则 X(k)=DFT[x(n)]N=ax (k)+bx2(k), k=0,1,2,.W-1 28

1．线性性质  设x1(n)，x2(n)为有限长序列，长度分别为 N N 1 2 、  它们的离散傅里叶变换分别为 1 1 ( ) [ ( )] ( ) [ ( )] max[ ] X N k DFT x n X k DFT x n N N N     若 2 2 12 ( ) [ ( )] max[ , ] X k DFT x n N N N   N x n ax n bx n () () ()    则 1 2 x n ax n bx n () () ()   1 2 ( ) DFT[ ( )] ( ) ( ) , 012 1 X k x n aX k bX k N k N    28 k N  0,1, 2, 1