
例1 设函数f(x)=sinx,求(sinx)'及(sinx)' 上页 下页 返回
6 例1 ( ) sin , (sin ) (sin ) . 4 π = = ′ ′ x 设函数 f x x 求 x 及 x 解

★定义2.3单侧导数 1.左导数: f(xo)=lim f(x)-f(xo) lim f(x+△)-fx: x-xo △x→0 △x 2.右导数: (xo)=lim fw)-fx)=lim f(x+△x)-f(xo) x→x0 x-xo △x→0+ △x ★函数fx)在点x,处可导一左导数f(x)和右导 数f(x。)都存在且相等. ★如果f(x)在开区间(a,b)内可导,且f(a)及 '(b)都存在,就说f(x)在闭区间[a,b上可导 上页 返回
7 ★ 2.右导数: 定义2.3 单侧导数 1.左导数: ; ( ) ( ) lim ( ) ( ) ( ) lim 0 0 0 0 0 0 0 x f x x f x x x f x f x f x x x x ∆ + ∆ − = − − ′ = − → − → ∆ − ; ( ) ( ) lim ( ) ( ) ( ) lim 0 0 0 0 0 0 0 x f x x f x x x f x f x f x x x x ∆ + ∆ − = − − ′ = + → + → ∆ + 函数 f (x)在点x0处可导⇔左导数 ( ) x0 f − ′ 和右导 数 ( ) x0 f + ′ 都存在且相等. ★ ★ 如果 f (x)在开区间(a,b)内可导,且 f (a) + ′ 及 f (b) − ′ 都存在,就说 f (x)在闭区间[a,b]上可导

例2 讨论函数f(x)=x在x=0处的可导性. 解 上页 下页 返回
8 例2 讨论函数 f (x) = x 在x = 0处的可导性. 解

2.1.3可导与连续的关系 定理2.1若f(x)在x,点可导,则f(x)在x点连续 证 设函数f(x)在点x,可导, lim A=f(x) Ax-→0△X lim Ay=lim △x-→0 Ay.△x=f'x)0=0 Ax→0△x .函数f(x)在点x连续 注:连续是可导的必要非充分条件,即连续 函数并不一定可导,但不连续函数必不可导. 上贡 返回
9 定理 2.1 证 ( ) , 设函数 f x 在点 x0可导 lim ( ) 0 0 f x x y x = ′ ∆ ∆ ∆ → 0 0 0 0 0 ⋅∆ = ′ ⋅ = ∆ ∆ ∆ = ∆ → ∆ → lim lim x f (x ) x y y x x 函数 ( )在点 连续 . 0 ∴ f x x 注: 连续是可导的必要非充分条件,即连续 函数并不一定可导,但不连续函数必不可导. 若 ( )在 点可导,则 ( )在 点连续. 0 0 f x x f x x 2.1.3 可导与连续的关系
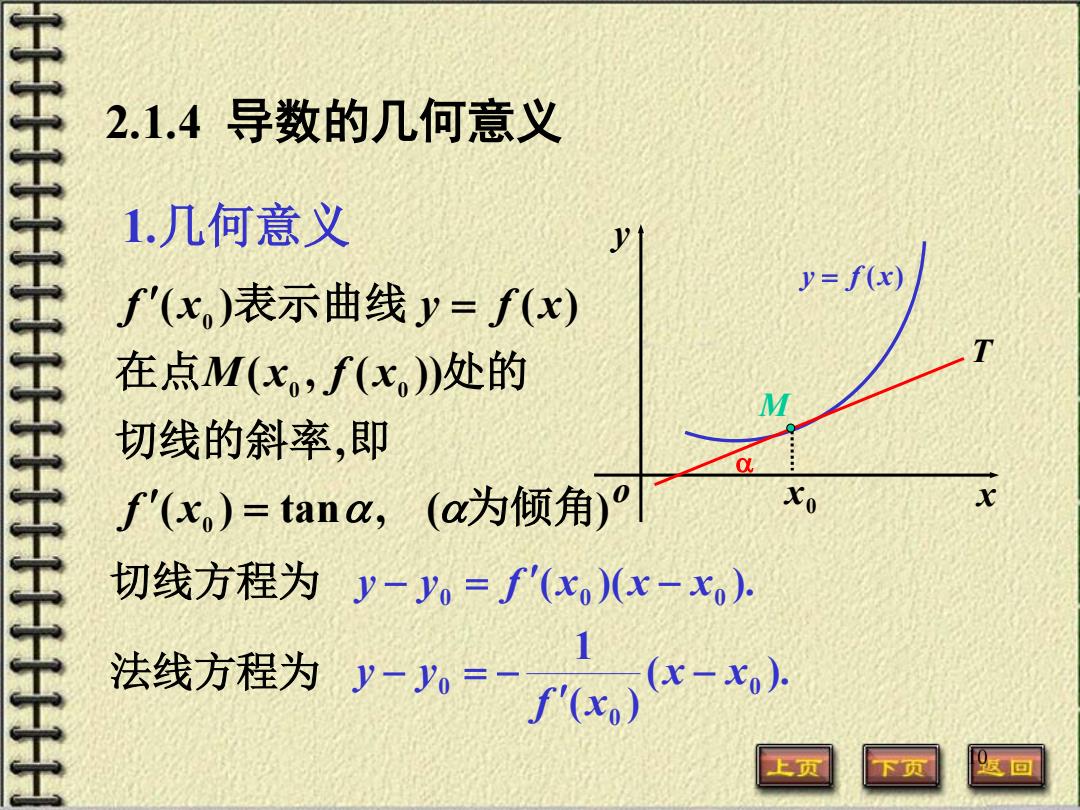
2.1.4导数的几何意义 1.几何意义 f'(x,)表示曲线y=f(x) Y-f(x) T 在点M(x,f(x。)处的 M 切线的斜率,即 f'(x,)=tana,(a为倾角)° Xo X 切线方程为y-y,=f'(x)(x一x) 法线程为y-f代 上页 9返回
10 2.1.4 导数的几何意义 o x y y = f (x) α T x0 M 1.几何意义 ( ) tan , ( ) , ( , ( )) ( ) ( ) 0 0 0 0 为倾角 切线的斜率 即 在点 处的 表示曲线 ′ = α α ′ = f x M x f x f x y f x 切线方程为 法线方程为 ( )( ). 0 x0 x x0 y − y = f ′ − ( ). ( ) 1 0 0 0 x x f x y y − ′ − = −