
(三)静电场的高斯定理 面新 一、选择题与填空题: 1.点电荷Q被曲面S所包围,从无穷远处引人另一点电荷q至曲面外一点,则引入前 后: (D) (A)曲面S的电通量不变,曲面上各点E不变; (B)曲面S的电通量变化,曲面上各点E不变; (C)曲面S的电通量变化,曲面上各点E变化: (D)曲面S的电通量怀变曲面上各点E变化。 2.对于静电场中的高斯定理,以下几种说法中正确的是 (A)如果高斯面上E处处为零,则该面内必无电荷; (B)如果高斯面内无电荷,则高斯面上E处处为零; (C)如果高斯面上E处处不为零,则高斯面内必有电荷: (D)如果高斯面内有电荷,则高斯面上E处处不为零; (E)以上说法都不正确。 3.对于下列带电系统,哪些可以直接用高斯定理求电场强度分布? (AD (A)无限长均匀带电直线或无限长均匀带电圆柱面: (B)有限长均匀带电线段; (C)均匀带电圆环; (D)均匀带电球面或球体。 4.有两个点电荷电量都是q,相距为2a,今以左边的点电荷所在处为球心,以a为半径 作一球形高斯面,在球面上取两块相等的小面积S,和S2,其位置如图的所示,设通过S,和 S2的电场强度通量分别为④,和中2,通过整个球面的电场强度通量为Φ,则 (A) (A)Φ1>Φ2,Φ.=q/e0 (B)Φ1<Φ2,④,=2q/e (C)重1=Φ2,④,=q/0 (D)④1<Φ2,Φ,=q/eo +0 9 2a 1
(三 )静 电场的高斯定理 -、 选择题与填空题: 1.点 电荷 Q被曲面 s所包围,从无穷远处引人另一点电荷 q至曲面外一点,则 引人前 后: (A)曲 面 s的 电通 鳓 面|各卢 它不变; (B)曲 面 S的电通量变化,曲 面上各点 它不变; (C)曲 面 s的电通量变化,曲 面上各点 宦变化; (D)曲 面 s的电通酬 乩面上各点 宦变化。 2.对于静电场中的高斯定理,以 下几种说法中正确的是 (A)如 果高斯面上 宦处处为零,则该面内必无电荷; (B)如果高斯面内无电荷,则高斯面上 宦处处为零; (C)如果高斯面上 宦处处不为零,则 高斯面内必有电荷; (D)如 果高斯面内有电荷,则 高斯面上 宦处处不为零; (E)以上说法都不正确。 3.对于下列带电系统,哪些可以直接用高斯定理求电场强度分布? (A)无限长均匀带电直线或无限长均匀带电圆柱面; (B)有 限长均匀带电线段; (C)均匀带电圆环; (D)均匀带电球面或球体。 4.有两个点电荷电量都是 q,相距为2a,今 以左边的点电荷所在处为球心,以 a为半径 作一球形高斯面,在球面上取两块相等的小面积 s1和 S2,其 位置如图的所示,设通过 s1和 s2的 电场强度通量分别为 Φ1和 Φ2,通 过整个球面的电场强度通量为 Φs,贝刂 (A) (∶ I∶ ;冫 ) (~F) (ω) ·1· (A)Φ1)Φ2,Φ :〓 q/co (C)Φ 1〓 Φ2,Φ$=q/go (B)Φ1<Φ2,Φ s=2q/e。 (D)Φl<Φ2,Φ s=q/e

二、计算题: 1.两无限长同轴圆柱面,半径分别为R1及R2(R2<R,),带有等量异号的电荷,外柱面 带正电,内柱面带负电。电荷线密度为±入。试分别求出(1)r<R2;(2)r>R1;(3)R2<r< R时,离轴线为r处的场强。并画出E~r曲线。 r<R, E=0 A<rk,E=-a Y r>B E-0 中高 2.两个同心的均匀带电球面,半径分别为R1,R2,带电量分别为Q和Q2,求电场强度 的分布。 Y∠R E=0 ,<Y<22 E-6 4领oY2 丫>2, E之Q+仅, 4T。Y2 2
二、计算题: 1.两无限长同轴圆柱面,半径分别为 R1及 R2(凡 <R1),带有等量异号的电荷,外柱面 带正电,内 柱面带负电。电荷线密度为 ±λ。试分别求出(1)r<R2;(2)r>R1;(3)R2(r< R1时 ,离轴线为 r处的场强。并画出E~r曲 线。 ∷ ∷ r《 R⊥ L二。 / 赵ˉ<改浅∴L||纭 叮>民 -匚△ 2.两个同心的均匀带电球面,半径分别为R1,R2,带 电量分别为Qi和 Q∶ ,求 电场强度 的分布。 丫《泛丨 ε三口 泛l<r‘ R亠 E≥ 丫》R⊥ ∴Ⅱ ∷庄 丁 ∷ H-TI色 丫 L ·2·
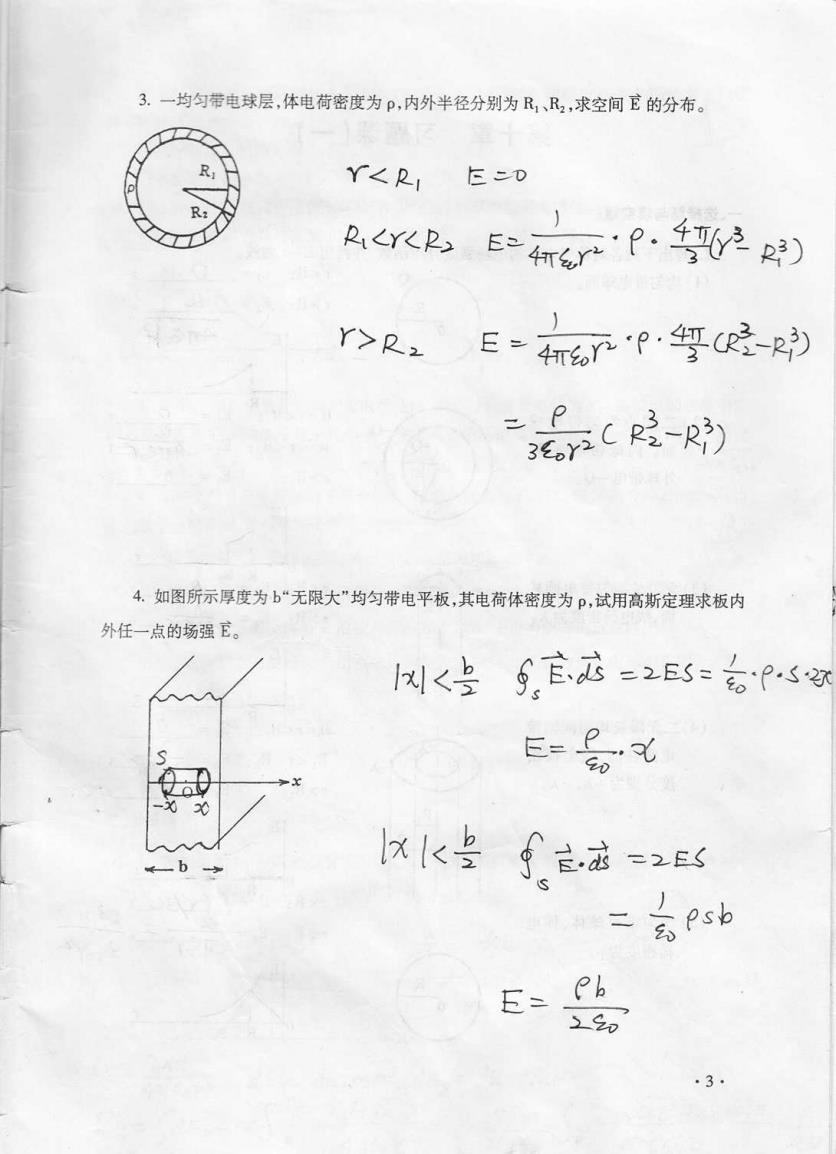
3.一均匀带电球层,体电荷密度为P,内外半径分别为R1、R2,求空间卫的分布。 Y<2 E二D arE产p0产 r>R2 Erp停-的 2- 4.如图所示厚度为b“无限大”均匀带电平板,其电荷体密度为P,试用高斯定理求板内 外任一点的场强E。 风<当写,官店=2B=名Ps E-0 -X 20 eb kk f应 -2E< 二 高Psb E=- h ·3
殳 ← 蓬 县 哀 ‘llI﹁ Ⅱ 〓 ﹁ ﹁ 〓 ~;︱ 〓 汊甜 `↓ 3.一均匀带电球层,体电荷密度为 ρ,内外半径分别为 R1、 R2,求空间它的分布。 4.如 图所示厚度为 b“ 无限大 ”均匀带电平板,其 电荷体密度为 ρ,试用高斯定理求板内 外任一点的场强 宦。 工R⒎9 h|<去 免:砝 二廴Es=圭 c卩 ·“娥 I::∶∶:〓〓L~ˉ弯:∶∶;F,· 钇 匚 … Fˉ石歹=∶ ':兰 姒淬珲D ) E:=〓 亠 :<.{}∶ I冂 :∶ lo∶{氵 冫r》 卩 · 飞瑾击C咩 亡。庇ˉi“ ∷△ 瓦 阝妇 Eˉ 1篷》 r<良 丨 良1‘rCIb r>R亠 |% 怨涪 巾 b丁 f§ < 一 一 ·3· ← b ~
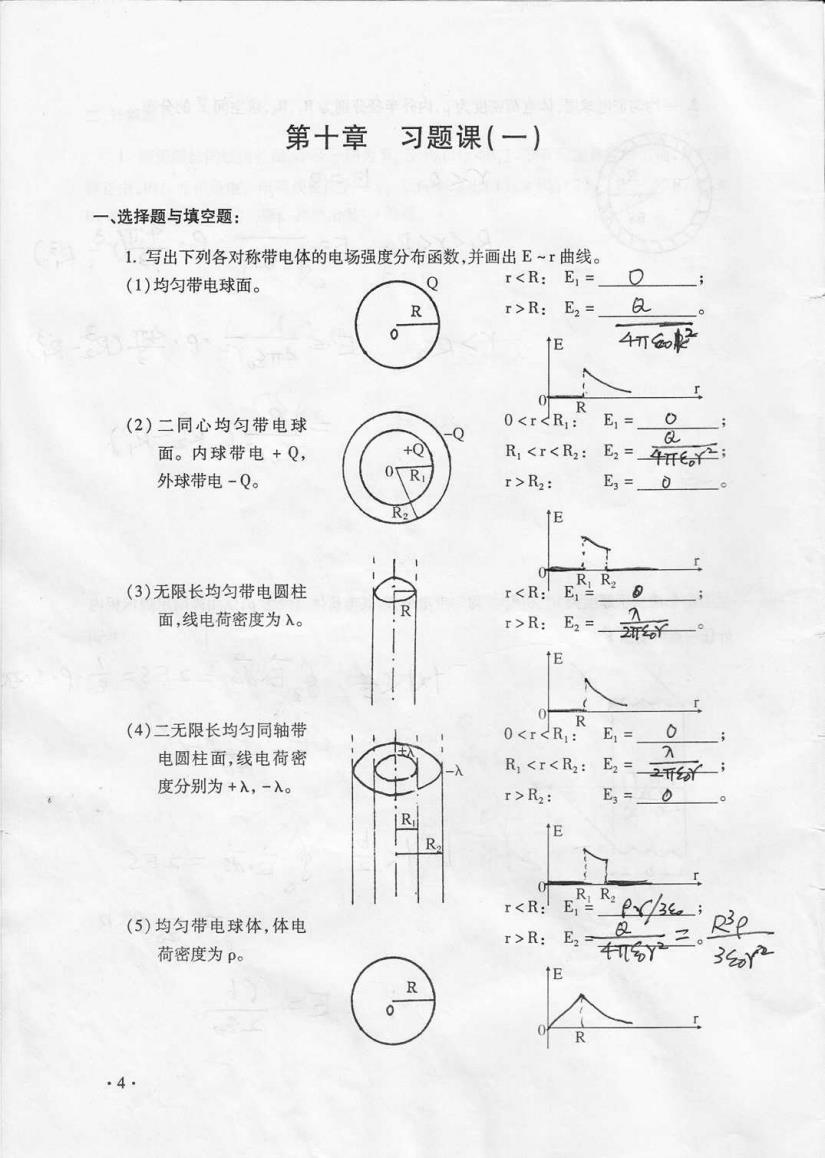
第十章习题课(一) 一、选择题与填空题: 1.写出下列各对称带电体的电场强度分布函数,并画出E~r曲线。 (1)均匀带电球面。 Q r<R:E=O R r>R:E2= 久 0 E 4TT o (2)二同心均匀带电球 0<R E,= & 面。内球带电+Q, +0 R<r<R:E,=4开o千 外球带电-Q。 r>R2: E3=0 ↑E (3)无限长均匀带电圆柱 <R:ERR O 面,线电荷密度为入。 r>R: E (4)二无限长均匀同轴带 R 0<r<R1 E=0 电圆柱面,线电荷密 R1<r<R2: 度分别为+入,-入。 B,=2开研 r>R2: E3=。 R ↑E (5)均匀带电球体,体电 r>R: 荷密度为p。 E2 Y 3产 E R ·4
第十章 习题课 (-) -、选择题与填空题: 1.∷ 写出下列各对称带电体的电场强度分布函数,并 画出E~r曲 线。 (1)均 匀带电球面。 (2)二 同心均匀带 电球 面。内球带 电 +Q, 外球带电-Q。 (3)无限长均匀带 电圆柱 面,线 电荷密度为 λ。 (4)二 无限长均匀同轴带 电圆柱面9线 电荷密 度分另刂为 +λ ,-λ 。 (5)均 匀带 电球体,体 电 荷密度为 ρ。 r(R: E1= t9 ; r>R: E2〓 艮 。 r>R2: E3=_o__ˉ 。 E亠 R2夕 黾 〓 苷 一λ R1(r(R2: r>R1: 马 〓 轹 ; E3〓 D 。 E Z钎铴扩 0<r<Rl: E1= 0 ; ` r △巛△:岛 =縻撬昏 。4·