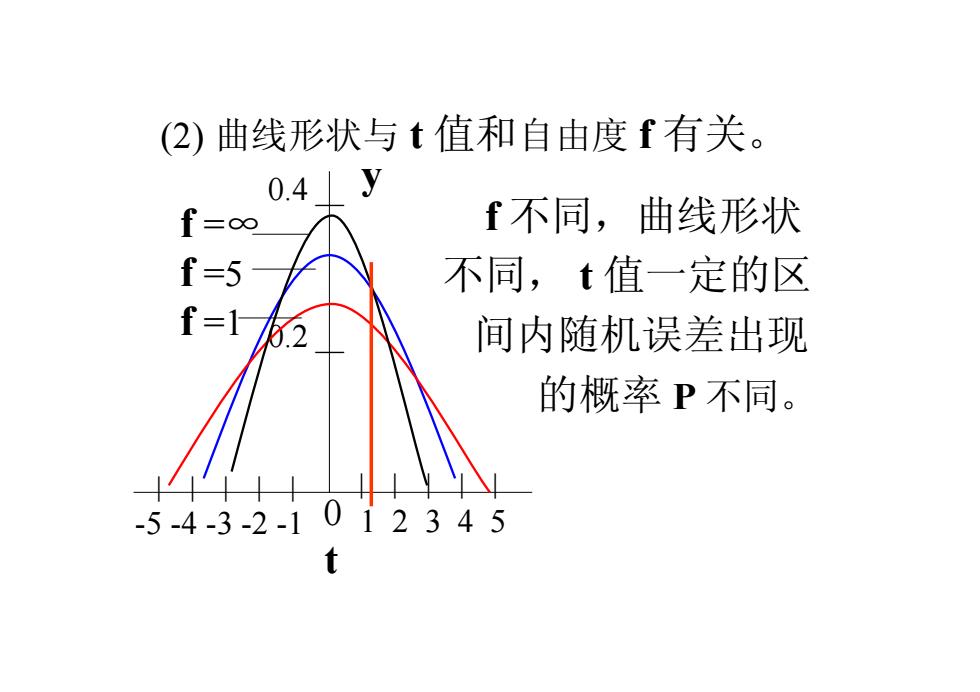
(2) 曲线形状与 t 值和自由度 f 有关。 y 0 t 0.4 _ | | | | | 1 2 3 4 5 | | | | | -5 -4 -3 -2 -1 0.2 _ f 不同,曲线形状 不同, t 值一定的区 间内随机误差出现 的概率 P 不同。 f =1 f =5 f =∞
(2) 曲线形状与 t 值和自由度 f 有关。 y 0 t 0.4 _ | | | | | 1 2 3 4 5 | | | | | -5 -4 -3 -2 -1 0.2 _ f 不同,曲线形状 不同, t 值一定的区 间内随机误差出现 的概率 P 不同。 f =1 f =5 f =∞

3、 值表: f tα, 体现 t , f , P 之间的关系 已知 f , P 时,可从表中查出相应的 t 值。 表中置信度就是概率 P , 它表示 t 值一定时,测定值落在 (μ ± t ⋅s) 范围内的概率。 显著性水准 α =1− P 自由度 f = n −1, n 为测定次数 双边:表示P是从-t到+t积分而得的面积
3、 值表: f tα, 体现 t , f , P 之间的关系 已知 f , P 时,可从表中查出相应的 t 值。 表中置信度就是概率 P , 它表示 t 值一定时,测定值落在 (μ ± t ⋅s) 范围内的概率。 显著性水准 α =1− P 自由度 f = n −1, n 为测定次数 双边:表示P是从-t到+t积分而得的面积

7.3.2 平均值的置信区间 1、置信区间的计算公式 根据 xs x t − μ = 可得计算公式 n ts x t s x μ = ± ⋅ x = ±
7.3.2 平均值的置信区间 1、置信区间的计算公式 根据 xs x t − μ = 可得计算公式 n ts x t s x μ = ± ⋅ x = ±

2、置信区间的概念 n ts x t s x μ = ± ⋅ x = ± 它表示在一定置信度下,以平均值 为 中心,包括总体平均值 的范围。 x μ 是客观存在的,没有随机性,不能说 它落在某一区间的概率是多少;只能说某 区间包括总体平均值的概率是多少。 μ
2、置信区间的概念 n ts x t s x μ = ± ⋅ x = ± 它表示在一定置信度下,以平均值 为 中心,包括总体平均值 的范围。 x μ 是客观存在的,没有随机性,不能说 它落在某一区间的概率是多少;只能说某 区间包括总体平均值的概率是多少。 μ

3、平均值置信区间的计算步骤 根据 n t s x f ⋅ = ± α, μ ①计算测量值的 x, s ②由置信度和测量值个数 n,计算出 α =1− P , f = n −1 ③将上述数据代入(1)式即可计算。 f t 从表 α, 7-3 查 分析化学中一般将置信度定在95%或90% 。 (1)
3、平均值置信区间的计算步骤 根据 n t s x f ⋅ = ± α, μ ①计算测量值的 x, s ②由置信度和测量值个数 n,计算出 α =1− P , f = n −1 ③将上述数据代入(1)式即可计算。 f t 从表 α, 7-3 查 分析化学中一般将置信度定在95%或90% 。 (1)