
飞号与素裂 §93连续时间系统状态方程的 建立 •状态方程的一般形式和建立方法概述 •由电路图直接建立状态方程 •由系统的输入-输出方程或流图建立状态方程 •将系统函数分解建立状态方程 共米 新疆大学信息科学与工程学院电子系 2003.1 退出 开始
新疆大学信息科学与工程学院电子系 2003.1 §9.3 连续时间系统状态方程的 建立 •状态方程的一般形式和建立方法概述 •由电路图直接建立状态方程 •由系统的输入-输出方程或流图建立状态方程 •将系统函数分解建立状态方程
.状态方程的一 般形式和建立方法概述忽 一个动态连续系统的时域数学模型可利用信号的各阶导 数来描述。作为连续系统的状态方程表现为状态变量的 联立一阶微分方程组,即 {26,} or,(t) or(t) m个输入信号 个输出信号 入(d),入(d,(d为系统的k个状态变量。 合U
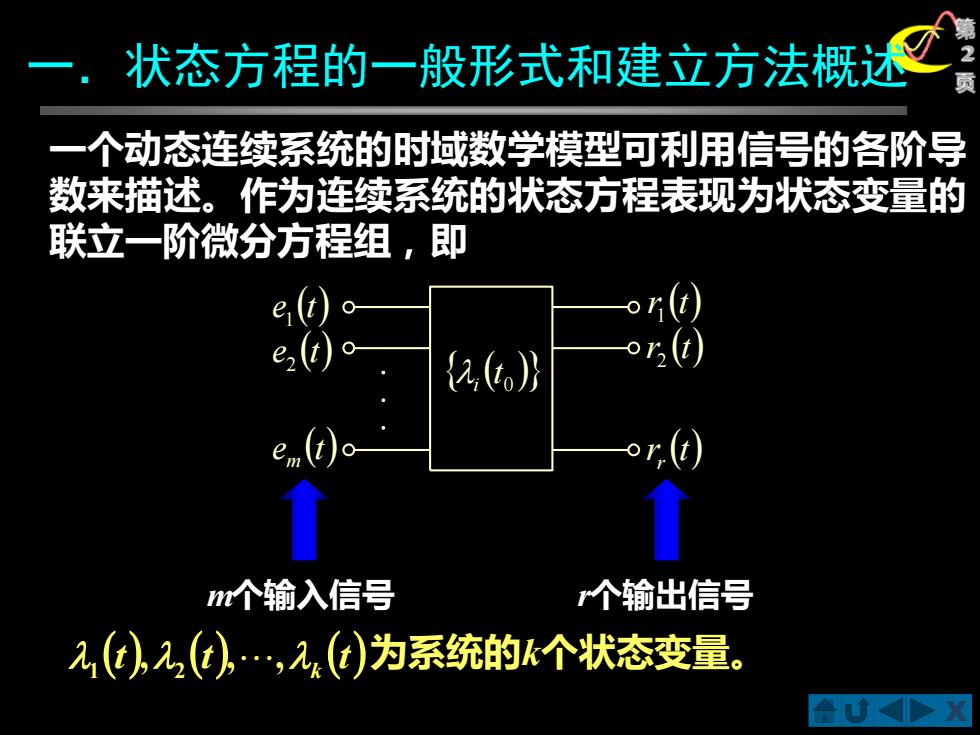
X 第 2 一.状态方程的一般形式和建立方法概述 页 一个动态连续系统的时域数学模型可利用信号的各阶导 数来描述。作为连续系统的状态方程表现为状态变量的 联立一阶微分方程组,即 e (t) 1 e (t) 2 e (t) m . . . r (t) 1 r (t) 2 r (t) r i (t 0 ) (t) (t) (t) k , , , 1 2 为系统的k个状态变量。 m个输入信号 r个输出信号

状态方程 20=[02,0.e0.e00.] dt -k4rege则 出小=k2-ee.d 输出方程 r0)=h[a),0,)ee),en), 5)=h,[a②)2,.,)ee,en, 0)=h[2,0z0,Ae0.e0e0. >】
X 第 3 状态方程 页 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = = = t f t t t e t e t e t t t t f t t t e t e t e t t t t f t t t e t e t e t t t k k k m k m k m , , , ; , , , , d d , , , ; , , , , d d , , , ; , , , , d d 1 2 1 2 2 2 1 2 1 2 1 1 1 2 1 2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = = = r t h t t t e t e t e t t r t h t t t e t e t e t t r t h t t t e t e t e t t r r k m k m k m , , , ; , , , , , , , ; , , , , , , , ; , , , , 1 2 1 2 2 2 1 2 1 2 1 1 1 2 1 2 输出方程

如果系统是线性时不变的,则状态方程和输出方程是 状态变量和输入信号的线性组合,即: 40=a20-a20ta40 +be0)+be)+.bmen) 20=a20*a20++a3间 +be1)+b2e2)+.zmEm()t 0=a2+a0++a +b1e1d)+be2e2)+.bnen(t)
X 第 4 页 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) + + + = + + + + + + = + + + + + + = + + + b e t b e t b e t t a t a t a t t b e t b e t b e t t a t a t a t t b e t b e t b e t t a t a t a t t k k km m k k k kk k m m k k m m k k 1 1 2 2 1 1 2 2 2 1 1 2 2 2 2 2 2 1 1 2 2 2 2 1 1 1 1 2 2 1 1 1 1 1 1 2 2 1 d d d d d d 如果系统是线性时不变的,则状态方程和输出方程是 状态变量和输入信号的线性组合,即:
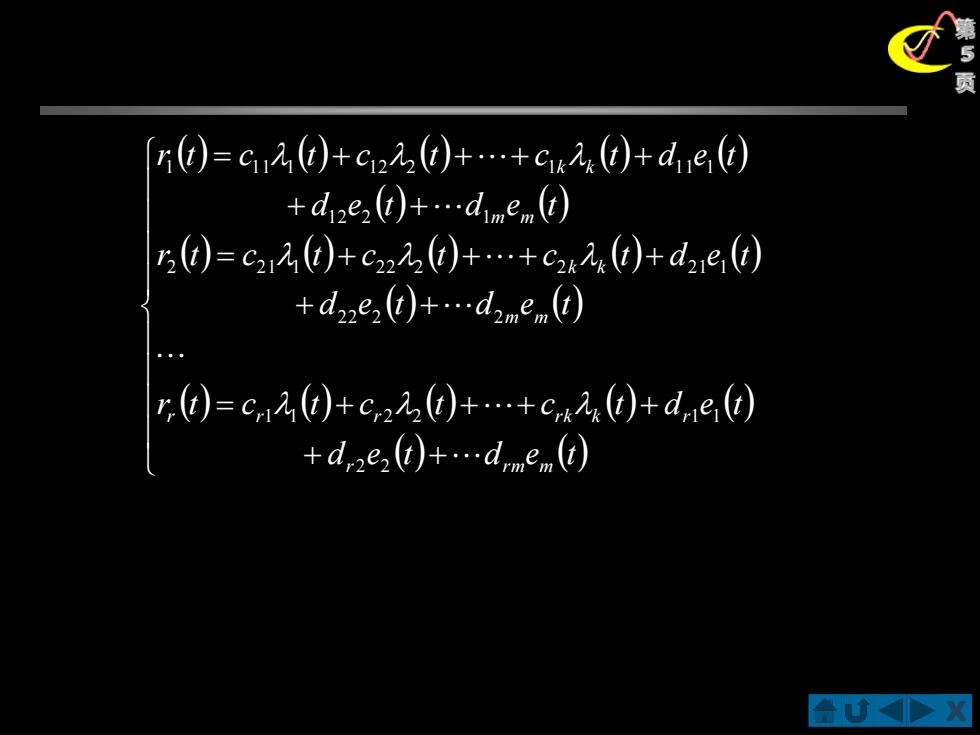
[r0)=c0)+c20)+.+cs,☑+de +d2e2d)+.dmen (t) 5d)=c212)+c2)++c2s)+d2,e) +d2e)+.dnen) r园=c20+c✉0++cw,)+ded
X第5页 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) + + = + + + + + + = + + + + + + = + + + + d e t d e t r t c t c t c t d e t d e t d e t r t c t c t c t d e t d e t d e t r t c t c t c t d e t r r m m r r r r k k r m m k k m m k k 2 2 1 1 2 2 1 1 2 2 2 2 2 2 1 1 2 2 2 2 2 1 1 1 2 2 1 1 1 1 1 1 2 2 1 1 1 1