
此吸引域延伸到系统的不稳定平衡点x°。参照式(21),在x°与x“之间的区域内,由于 电磁功率P大于机械功率P,所以电动机将加速(转差将减小)并最终回到稳定平衡点 对于大量的恒温控制的加热负荷,相应的方程式为 7=P.-G (2-2) 同感应电动机的情况类似,系统在大干扰后要保持稳定,对应于系统达到最终结构 (即故障线路恢复,并联电容器重新投入)时刻的电导必须在系统稳定平衡点x的“吸引 域”之内,此吸引域延伸到系统的不稳定平衡点x。参照式(2-2),在x与x”之间的区 域内,由于G大于P。,恒温负荷将减小其等值电导(增加电压),并最终回到x点。 对于变压器分接头的情况也类似。事实上,改变相应方程式的形式后仍可使用式(2 2),此时G表示按分接头位置对应的实际变比折算到高压侧的负荷电导。 2.3电压稳定性与功角稳定性的关系 电压稳定性和功角(同步)稳定性之间有一定内在联系,暂态电压稳定通常与暂态功 角稳定有联系,而变化过程缓慢的电压稳定则与小干扰功角稳定有关。在通常情况下,两 者很难从机理上完全分开。 当然,在许多情况下某种失稳形式占主导地位。EEE报告[9]中给出了两种极端情况: ①远方的一台同步发电机通过输电线路接入无穷大系统(纯功角稳定—单机无穷大母 线问题);②一台同步发电机或一个无穷大系统通过输电线接有异步负荷(纯电压稳定问 题)。图25(a)、(b)分别表示上述两种极端情祝。 ⊙ 大系烷 (a) 大系统 图2-5表示稳定问题板端情况的简单系统 (》纯功角稳定:(b)钝电压稳定 功角稳定与电压稳定均受无功控制的影响。特别是在连续动作的发电机自动电压调节 17 器出现之前,涉及到功角非周性增加的小干扰(静态)失稳是一个主要问题。小干扰功角 稳定和长期电压稳定之间存在一定联系:发电机电流限制(过励磁限制器)会阻止自动电 压调节器的正常工作,而发电机的电流限制对两种形式的稳定问题都极为不利。 电压稳定性问题主要涉及负荷区域与负荷特性。而就功角稳定性而言,通常关心经过 稳定性 长距离输电线路接入大系统的远方发电厂。因此,电压稳定本质上属于负荷稳定问题,而 功角稳定则本质上为发电机稳定问题。 对于大型互联电力系统,在所有发电机保持同步运行的前提下,负荷区域有可能发生

电压崩溃。 暂态电压稳定通常与暂态功角稳定密切相关,而长期电生稳定与功角稳定之间则关系 不大。 一般而言,如果在远离负荷的输电系统某点电压发生崩遗,这是一个功角失稳问题: 而如果在负荷区域某点电压发生崩遗,则可能主要是电压失稳问题。 2.4饱和电力系统中的电压失稳问题 一般认为发展中的电力系统容易出现电压问题。同样,系统解列后会引起电压稳定性 问题。但是,最近人们开始关注一些饱和电力系统的电压稳定性问题。 原因之一是目前许多电力公司都在最大限度地利用现有发电设备和输电线路。因为在 负荷中心难以建新电厂,而在远方电厂与负荷中心之间新架输电线路也十分闲难。 原因之二是大量应用并联电容器组进行无功补偿。大量使用并联电容器组后,在增 加线路传输功率极限的同时,也使电力网络更容易发生电压崩溃。因为并联电容器组的 无功输出与电压平方成正比,故使系统在电压稳定问题上显得更加脆弱。 由于快速故障切除装置、高性能励磁系统、电力系统稳定器和其他控制措施有效地缓 解了系统的暂态稳定性问题,热容量或电压稳定随之成为限制系统传输功率极限的主要因 素。下面的示例将说明饱和电力系统如可何会存在电压微定性问题。 【例21】图2-6表示有5条500kV线路的输电系统,其不存在暂态稳定性问题。至于 热极限问题,当一条线路开断后,其余4条线路传输的功率将分别增加25%。超高压长 线路的负荷一般低于波阻抗功率的1.5倍,而线路的热极限通常约为波阻抗功率的3倍。 因此和发展中的输电系统情况不同(只有2条或3条线路),热极限很少成为限制因素, 输电线路的利用率较高。 现在考虑5条输电线路对电力系统电压稳定性问题的影响,其中涉及到和电流平方有 关的非线性关系式(严X为线路申联电抗的无功损耗)。在波阻抗功率附近,每条线路的 电流为1000A,开断一条线路将使串联电抗的无功损耗由1200Mvr(5条线路×3相× 1000×80n)上升到1500Mvar,增加了300Mvar。考虑到负荷经过多年的增长,线路具有 较高的利用率。线路正常时的工作电流为1S00A,此时若开断一条线路将使申联无功损耗 18 由2700Mvar上升到3375Mvar,即增加675Mvr,或者讲相当于波阻抗功率的225%。同理 可以计算开断2条线路时的情形。实际上,由于开断线路后负荷侧电压降低,还将增加线 电 发电区域 负区 森教为纳长克 图26表示具有5条输电线路的饱和电力系统

路串联电抗的无功损耗[参见式(1-)],同时减小线路并联电容提供的无功功率。以上 计算屮尚未考虑这些因素,考虑这些因素后系统的情况将更加恶化。由于这些非线性因素 的影响,电压稳定性问题在系统建成仅数年之后就可能出现。 2.5电压稳定性分析方法介绍:P-V曲线 变化过程缓慢的电压失稳通常作为静态问题来分析,主要的研究手段是潮流仿真。主 要仿真电力系统在元件开断后或负荷增长过程中各运行点的变化过程。除计算电力系统扰 动后的潮流之外,还广泛应用两类基于潮流的分析方法:P一V曲线法和V-Q曲线法 这两类方法用于确定和电压稳定性有关的系统静态负荷极限。应用常规潮流计算程序可近 似分析电压稳定性问题。 应用P·V曲线便于从概念上分析电压稳定性问题以及研究辐射型输电系统。此方法 也可以应用于大型互联系统,这时P通常表示某区域的总负荷,也可代表系统传输断面 或者区域联络线上的传送功率,V则为关键母线或具有代表性母线的电压,即可同时画出 几个母线的电压曲线。此方法存在两个缺点,一是潮流计算在接近曲线拐点或者称为最大 功率点处将会发散,二是当区域负荷增加时系统各发电机的出力必须按实际情况进行调 作为从概念上分析的一种方法,P-V曲线法便于考虑负荷随电压而变化的特性。例 如对一个电阻负荷,可以根据关系式Pm=21R来作出P-V曲线;另外一种极端情况 为恒功率(和电压无关)负荷0,在P-V曲线上表示为一条垂直线。2.7节将对此作进 一步论述。 首先以恒阻抗负荷作进一步解释。由电路理论可知,当负荷阻抗与电源内阻抗的模相 等时,线路传输功率最大。对于高阻抗(低导纳)负荷,系统运行在高电压、小电流区 域;相反,对于低阻抗(高导纳)负荷,系统运行在低电压、大电流区域。Barhier和Ram 在文献[16]中给出了相应的数学表达式。对于由一个电抗性网络和电阻负荷组成的最简单 情况,图27表示系统接线图,并给出了电压、电流和功率间的关系曲线。如前所述,当 负荷阻抗与电源内阻抗的模相等时线路传输功率最大,功率最大点对应的电压称之为临界 电压。 【例2-2】对于图2-7所示的简单戴维南等值系统,设负荷的功率因数为1。试求表达 式P:),并确定负荷最大功率和对应的电压(临界电压)。其中,将各变量以短路19 功率(E1X)为基准进行标准化,即 p=,g=.= 压稳定性 解将第1章中的有关公式改写为标准化形式,分别如下所示 念 。其有恒功率特性的静态负荷在实际中并不存在,应被重采用
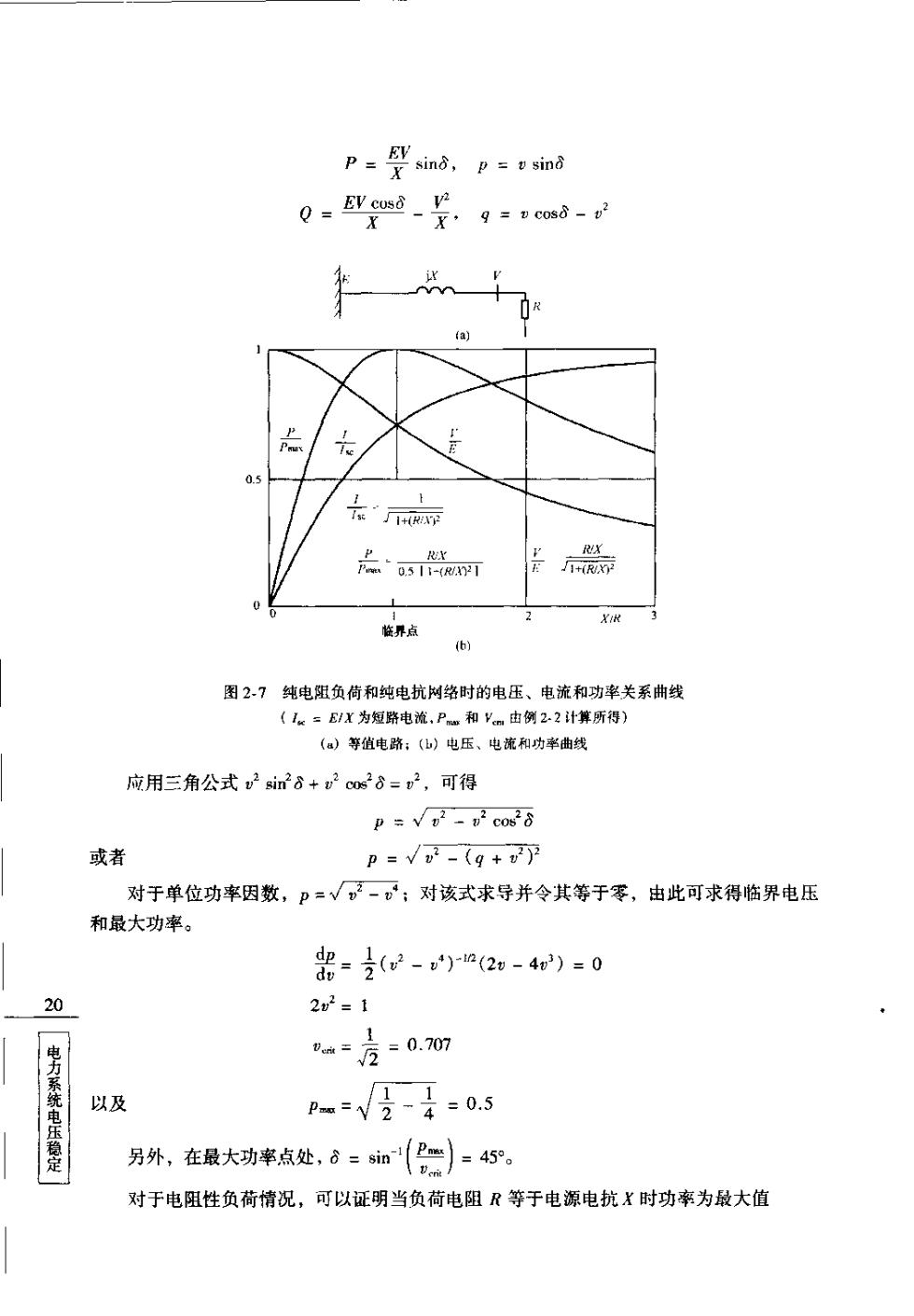
P=sing,p=sin 0 gind.co (a) 片' 品 器 2 界点 图27纯电阻负荷和纯电抗网络时的电压、电流和功率关系曲线 (1=E/X为短路电流,P和V由例2.2计算新得) ()尊值电路:(山)电压、电流和功率曲线 应用三角公式v2in28+D2cos28=p2,可得 psv c088 或者 p=√2-(g+ 对于单位功率因数,P=√。一。;对该式求导并令其等于零,由此可求得临界电压 和最大功率。 =2(d-)(2-4)=0 20 2x2=1 电力系统电压稳定 =方=0.m 以及 p=√分-4=0.5 另外,在最大功率点处,8=加(二=45。 对于电阻性负荷情况,可以证明当负荷电阻R等于电源电抗X时功率为最大值

P0.5v) =受=发 【例2-3】假设负荷为纯电抗,重复求解【例22】中的问题,并计算“电压崩遗邻 近指标(agec4 Pimit的yha,VCP)”(zH-品),其中Q,表示送罐发出的 无功功率,Q表示负倚无功功率。 解由于P=0和=0、因此有 0=兴-父 ¥=(E-2)=0 Vm=号 2张-发-发-2 同样可验证有关最人功率的理论,以标准化形式表示如下 tw=0.5 9-9=0.25 电压崩遗邻近指标(CPI)的计算方法如下 0=0+0=0+警 Q-0,+0=0 Q.=±s√-] 要品 21 由以上计算结果知,当系统由空载变化到最大负荷时,电压V的数值由E降为E2, 而VCP则从1增加到无穷大。这表明在接近最大负荷功率时,如果负荷功率有一微小增 压 量,则需要送端增加相当大的无功来满足负荷要求。因此CI可看作为系统逼近电压崩 遗的一种灵敏性指标,类似的灵敏性指标还有相应的无功备用的启用量和无功损耗大小。 对于简单模型,图2-8所示为一簇标准化的P-V曲线,分别对应不同的负荷功率因 数。功率因数越超前(通过并联补偿来获得超前的负荷功率因数),最大功率值越大,相 念 应的临界电压也越高。这是电压稳定性问题中非常重要的一个因素